- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Из истории параллельности прямых на плоскости
Содержание
- 2. Из истории математики известно, что вопрос параллельности
- 3. «Начала» Первым все знания с древних
- 4. «Начала»Основное сочинение Евклида называется «Начала». Книги с
- 5. В «Началах» Евклида была дана следующая аксиоматика:
- 6. «Начала»Аксио́ма паралле́льности Евкли́да, или пя́тый постула́т — одна из аксиом, лежащих в основании евклидовой планиметрии.
- 7. А дальше?На протяжении 2,5 тысяч лет вопрос
- 8. В течении первых же десятилетий XIX в.
- 9. К открытию новой, так называемой «неевклидовой», геометрии
- 10. Карл Фридрих Гаусс (1777-1855) — немецкий математик,
- 11. Янош БойяиВенгерский математик, сын математика
- 12. Из письма Франкаша Бойяи сыну:«Ты должен бросить
- 13. После смерти Бойяи были обнаружены более
- 14. Н.ЛобачевскийИ стояла геометрия ЕвклидаКак египетская чудо-пирамида. Строже
- 15. Первый набросок новой теории — доклад «Сжатое
- 16. В 1829 году журнал "Казанский вестник" опубликовал
- 18. Лобачевский умер непризнанным. Спустя несколько десятилетий ситуация
- 19. «Чем отличается геометрия Лобачевского от геометрии Евклида?»
- 20. Появление модели Клейна доказало, что геометрия Лобачевского
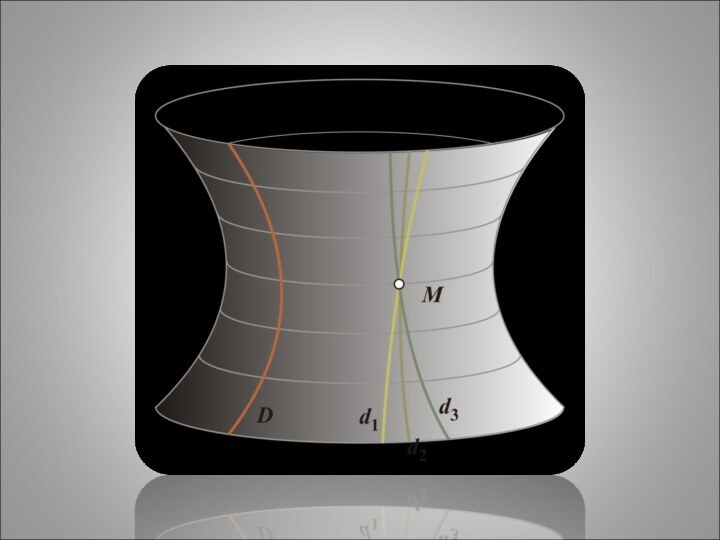
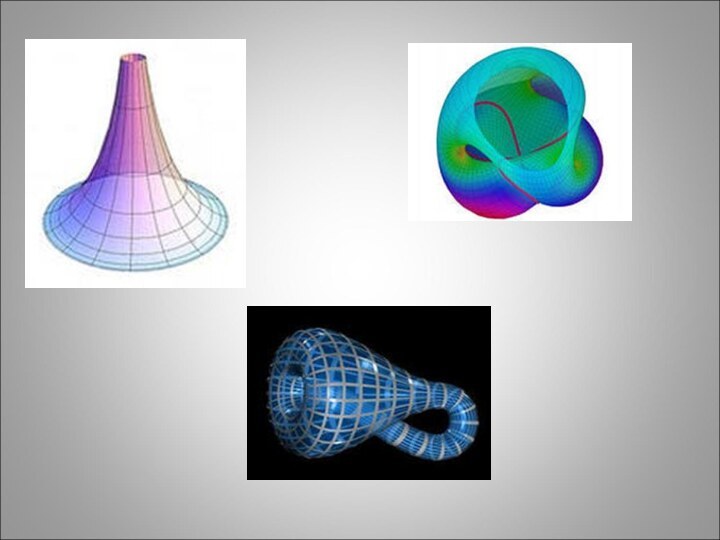
- 21. Поверхности, на которых действует неевклидова геометрия
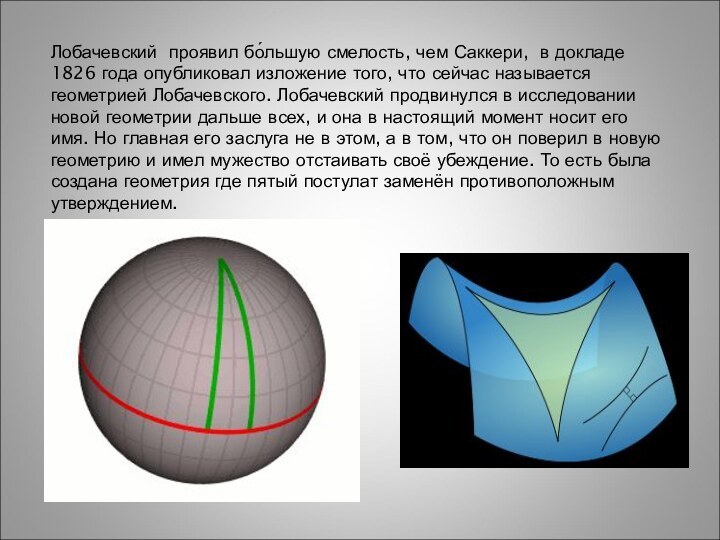
- 22. Лобачевский проявил бо́льшую смелость, чем Саккери, в
- 24. Скачать презентацию
- 25. Похожие презентации
Из истории математики известно, что вопрос параллельности прямых вызывал интерес математиков в течение двух с половиной тысяч лет.


















Слайд 3 «Начала» Первым все знания с древних времен о параллельности
прямых
обобщил ЕВКЛИД.
Евкли́д или Эвкли́д ( ок. 300 г. до
н. э.) — древнегреческий математик, автор первого из дошедших до нас теоретических трактатов по математике. Достоверным можно считать то, что его научная деятельность протекала в Александрии в 3 в. до н. э.
Слайд 4
«Начала»
Основное сочинение Евклида называется «Начала». Книги с таким
же названием, в которых последовательно излагались все основные факты
геометрии и теорети ческой арифметики, составлялись ранее Гиппократом Хиосским, Леонтом и Февдием. Однако Начала Евклида вытеснили все эти сочинения из обихода и в течение более чем двух тысячелетий оставались базовым учебником геометрии.
Слайд 5
В «Началах» Евклида была дана следующая аксиоматика:
От всякой
точки до всякой точки можно провести прямую.
Ограниченную прямую можно
непрерывно продолжать по прямой.Из всякого центра всяким раствором может быть описан круг.
Все прямые углы равны между собой.
Слайд 6
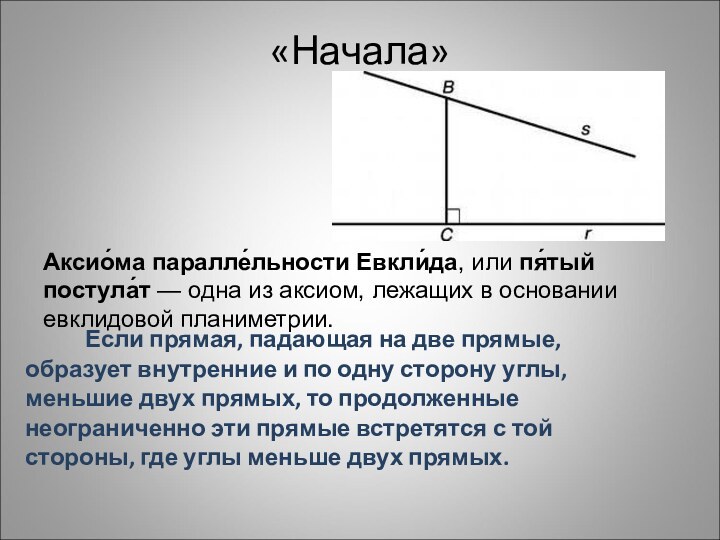
«Начала»
Аксио́ма паралле́льности Евкли́да, или пя́тый постула́т — одна
из аксиом, лежащих в основании евклидовой планиметрии.
Слайд 7
А дальше?
На протяжении 2,5 тысяч лет вопрос о
доказательстве постулата Евклида волновал умы математиков всего мира.
Среди них,
например были:Прокл
Птолемей
Ламберт
Хайям
Саккери и др.
Слайд 8
В течении первых же десятилетий XIX в. проблема
5-го постулата была решена несколькими лицами почти одновременно и
независимо друг от друга, но совершенно не так, как предполагали это прежние учёные: была создана новая геометрия, независимая от 5-го постулата.Слайд 9 К открытию новой, так называемой «неевклидовой», геометрии пришли
три человека:
1) профессор Казанского университета Николай Иванович Лобачевский (1792–1856);
2)
великий немецкий математик Карл Фридрих Гаусс (1777–1855);3) венгерский офицер Янош Бойяи (1802–1860).
Слайд 10
Карл Фридрих Гаусс
(1777-1855) — немецкий
математик, астроном,
геодезист и физик, иностранный член-корреспондент (1802) и иностранный почетный
член (1824) Петербургской АН.Что касается Гаусса, то он совершенно не оставил никаких следов систематического изложения своих открытий в области неевклидовой геометрии и при жизни не опубликовал ни одной строчки по этому вопросу. Гаусс слишком боялся уронить свой огромный авторитет в глазах учёного мира.
Слайд 11
Янош Бойяи
Венгерский математик,
сын математика
Фаркаша Бойяи.
Уже в колледже он
настолько увлёкся
исследованием пятогопостулата Евклида,
что отец встревожился за судьбу сына.
Слайд 12
Из письма Франкаша Бойяи сыну:
«Ты должен бросить это
как самое гнусное извращение. Оно может отнять у тебя
всё время, здоровье, разум, все радости жизни. Эта чёрная пропасть в состоянии, может быть, поглотить тысячу таких титанов, как Ньютон…»В 1832 году отец публикует своё сочинение, а в приложении к нему — работу сына, вошедшую в историю математики под именем Appendix (приложение). Полное название труда Яноша Бойяи: «Приложение, содержащее науку о пространстве, абсолютно истинную, не зависящую от истинности или ложности XI аксиомы Евклида «
Слайд 13 После смерти Бойяи были обнаружены более 20000
листов незаконченных математических рукописей. Однако «Аппендикс» так и остался
единственной его работой, напечатанной при жизни автора.(памятник отцу и сыну Бойяи в Венгрии)
Слайд 14
Н.Лобачевский
И стояла геометрия Евклида
Как египетская чудо-пирамида.
Строже выдумать
строенье невозможно,
Лишь одна была в ней глыба безнадежна.
Аксиома называлась
"параллели" Разгадать ее загадку не сумели.
И подумал Лобачевский;
"Но ведь связана с природой аксиома!
Мы природу понимаем поземному
Во Вселенной расстоянья неземные,
Могут действовать законы там иные!"
Да, конечно, да,
Доказывать бесцельно!
Параллельные пойдут непараллельно!..
Слайд 15
Первый набросок новой
теории — доклад
«Сжатое изложение
начал
геометрии» Лобачевский
сделал 11 (23) февраля 1826 года,
дата этого выступления считается днём рождения неевклидовой геометрии.Слайд 16 В 1829 году журнал "Казанский вестник" опубликовал сочинение
Лобачевского о неевклидовой геометрии. Работа называлась "О началах геометрии".
В отзыве на него известный математик академик М. В. Остроградский писал: "Автор, по-видимому, задался целью писать таким образом, чтобы его нельзя было понять. Он достиг своей цели: большая часть книги осталась столь же неизвестной для меня, как если бы я никогда не видел ее". Затем он развивал эти идеи во многих трудах, издававшихся не только на русском, но и на французском и немецком языках.Слайд 18 Лобачевский умер непризнанным. Спустя несколько десятилетий ситуация в
науке коренным образом изменилась. Большую роль в признании трудов
Лобачевского сыграли исследования Э. Бельтрами (1868), Ф. Клейна (1871), А. Пуанкаре (1883) и др.
Слайд 19
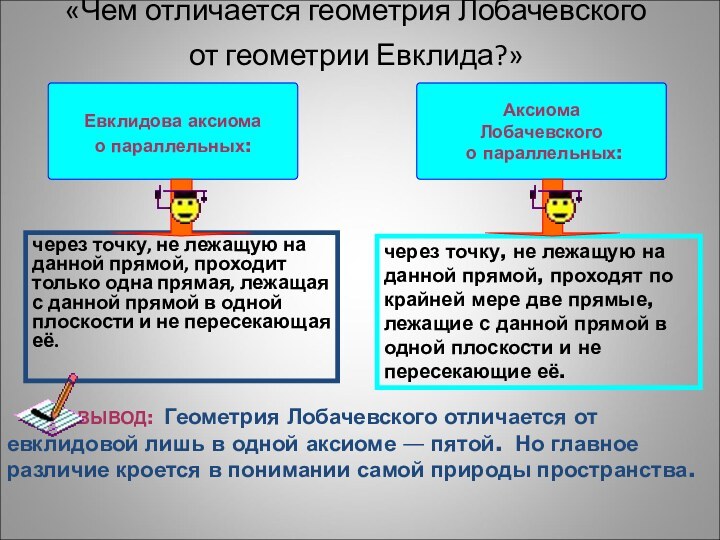
«Чем отличается геометрия Лобачевского
от геометрии Евклида?»
через точку,
не лежащую на данной прямой, проходит только одна прямая,
лежащая с данной прямой в одной плоскости и не пересекающая её.через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.
ВЫВОД: Геометрия Лобачевского отличается от евклидовой лишь в одной аксиоме — пятой. Но главное различие кроется в понимании самой природы пространства.
Евклидова аксиома
о параллельных:
Аксиома
Лобачевского
о параллельных:





























