Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Приемы решения логических задач презентация к уроку по математике по теме

Содержание

2. 1 Метод составления и решения уравненийАлгоритмПонять задачуСделать
3. 1 Метод составления и решения уравненийЗадача Летит
4. 1 Метод составления и решения уравненийРешениеX —
5. 2 Табличный способ решения логических задачАлгоритмНесколько раз
6. 2 Табличный способ решения логических задачЗадачаНа заводе
7. 2 Табличный способ решения логических задач
8. 3 Метод сведения сложной задачи к простойАлгоритмПредставить,
9. 3 Метод сведения сложной задачи к простойЗадачаМожно
10. 3 Метод сведения сложной задачи к простойРешениеПусть
11. 4 Решение задач на догадку и перебор
12. 4 Решение задач на догадку и перебор
13. 5 Метод фишек (метод линейного упорядочивания элементов
14. 5 Метод фишек (метод линейного упорядочивания элементов
15. 6 Методы решения задач на разрезания и
16. 6 Методы решения задач на разрезания и
17. 6 Методы решения задач на разрезания и распилы1 день2 день3 день4 день5 деньРешение
18. 6 Методы решения задач на разрезания и
19. 6 Методы решения задач на разрезания и распилыРешение
20. 7 Задачи на умение рассуждатьЗадачаМама хочет поджарить
21. 7 Задачи на умение рассуждатьРешениеНаименьшее количество времени
22. 8 Прием «Реши сначала частный случай»ЗадачаДаны 2
23. 8 Прием «Реши сначала частный случай»РешениеОтвет не
24. Скачать презентацию
25. Похожие презентации

1 Метод составления и решения уравненийАлгоритмПонять задачуСделать рисунокОпределить количество неизвестных и ввести обозначения (x, y, z)Составить уравненияПроследить, чтобы их количество равнялось числу неизвестныхРешить уравненияСделать проверку

Главная
Математика
Приемы решения логических задач презентация к уроку по математике по теме

Приемы решения логических задачКардашина С. Г. учитель начальных классов высшей кв.

1 Метод составления и решения уравненийАлгоритмПонять задачуСделать рисунокОпределить количество неизвестных и ввести

1 Метод составления и решения уравненийЗадача Летит стая гусей. Навстречу им летит

1 Метод составления и решения уравненийРешениеX — количество гусей в стаеX +

2 Табличный способ решения логических задачАлгоритмНесколько раз внимательно прочитать задачуОпределить количество множеств

2 Табличный способ решения логических задачЗадачаНа заводе работали три друга: слесарь, токарь

2 Табличный способ решения логических задач

3 Метод сведения сложной задачи к простойАлгоритмПредставить, что задача решена (метод решения

3 Метод сведения сложной задачи к простойЗадачаМожно ли, имея лишь два сосуда

3 Метод сведения сложной задачи к простойРешениеПусть задача решена, и в 5-литровом

4 Решение задач на догадку и перебор вариантовЗадачаВ ящике лежит много шариков

4 Решение задач на догадку и перебор вариантовВарианты1-й вариант: вынуть 2 шарика.

5 Метод фишек (метод линейного упорядочивания элементов множеств)ЗадачаВ очереди за билетами в

5 Метод фишек (метод линейного упорядочивания элементов множеств)РешениеЮ МО Ю МВ О

6 Методы решения задач на разрезания и распилыПравила, которые необходимо знать: количество

6 Методы решения задач на разрезания и распилыЗадачаПортной имеет кусок сукна длиной

6 Методы решения задач на разрезания и распилы1 день2 день3 день4 день5 деньРешение

6 Методы решения задач на разрезания и распилыЗадачаНа какое максимальное число кусков

6 Методы решения задач на разрезания и распилыРешение

7 Задачи на умение рассуждатьЗадачаМама хочет поджарить на завтрак дочке 3 гренки.

7 Задачи на умение рассуждатьРешениеНаименьшее количество времени уйдет, если сначала положить 1-ю

8 Прием «Реши сначала частный случай»ЗадачаДаны 2 одинаковых стакана. В одном вино,

8 Прием «Реши сначала частный случай»РешениеОтвет не зависит от количества перелитых жидкостей,

ЛитератураТамберг Ю.Г. Развитие интеллекта ребенка. — Екатеринбург: У-Фактория, 2004

Слайды презентации

Слайд 2 1 Метод составления и решения уравнений
Алгоритм
Понять задачу
Сделать рисунок
Определить

1 Метод составления и решения уравненийАлгоритмПонять задачуСделать рисунокОпределить количество неизвестных и

количество неизвестных и ввести обозначения (x, y, z)
Составить уравнения
Проследить,

чтобы их количество равнялось числу неизвестных
Решить уравнения
Сделать проверку

Слайд 3 1 Метод составления и решения уравнений
Задача
Летит стая

1 Метод составления и решения уравненийЗадача Летит стая гусей. Навстречу им

гусей. Навстречу им летит один гусь и говорит:
—

Здравствуйте, сто гусей!
— Нас не сто гусей, — отвечает вожак. — Если бы нас было столько, сколько теперь, и еще столько, да еще полстолько, да еще четверть столько, да еще ты, гусь, вот тогда бы нас было бы сто.
Сколько гусей было в стае?

Слайд 4 1 Метод составления и решения уравнений
Решение
X — количество

гусей в стае
X + X + 0,5X + 0,25X

+ 1 = 100
X = 36

Слайд 5 2 Табличный способ решения логических задач
Алгоритм
Несколько раз внимательно

2 Табличный способ решения логических задачАлгоритмНесколько раз внимательно прочитать задачуОпределить количество

прочитать задачу
Определить количество множеств в задаче и количество элементов

в каждом множестве
Составить таблицу с названиями множеств и элементов
Построить логические цепочки и заполнить таблицу безусловными данными («+» или «-»)
Искать невыясненные логические связи между элементами множеств до тех пор, пока все клетки не будут заполнены достоверной информацией

Слайд 6 2 Табличный способ решения логических задач
Задача
На заводе работали

2 Табличный способ решения логических задачЗадачаНа заводе работали три друга: слесарь,

три друга: слесарь, токарь и сварщик. Их фамилии: Борисов,

Иванов и Семенов.
Назовите фамилии слесаря, токаря и сварщика, если известно, что:
у слесаря нет ни братьев, ни сестер и он самый младший из друзей;
Семенов женат на сестре Борисова и старше токаря.

Слайд 7 2 Табличный способ решения логических задач

Слайд 8 3 Метод сведения сложной задачи к простой
Алгоритм
Представить, что

3 Метод сведения сложной задачи к простойАлгоритмПредставить, что задача решена (метод

задача решена (метод решения с конца)
Сформулировать другую, более простую

задачу
Использовать здравый смысл, догадку, перебор вариантов
Сделать рисунок или таблицу

Слайд 9 3 Метод сведения сложной задачи к простой
Задача
Можно ли,

3 Метод сведения сложной задачи к простойЗадачаМожно ли, имея лишь два

имея лишь два сосуда емкостью 3 и 5 литров,

набрать из водопроводного крана ровно 4 литра воды?

Слайд 10 3 Метод сведения сложной задачи к простой
Решение
Пусть задача

3 Метод сведения сложной задачи к простойРешениеПусть задача решена, и в

решена, и в 5-литровом сосуде 4 литра.
Для этого надо

слить 1 литр. Куда? В 3-литровый сосуд. Тогда в нем должно быть 2 литра воды. Как получить 2 литра?
Мы получили новую простую задачу. Чтобы ее решить, наполним 5-литровый сосуд, сольем 3 литра в 3-литровый и выльем эту воду — она нам не нужна. Перельем в опустевший 3-литровый сосуд оставшиеся в 5-литровом сосуде 2 литра.
Наполним еще раз 5-литровый сосуд, сольем из него волу в 3-литровый. В него сейчас может войти только 1 литр, поэтому в 5-литровом останется 4 литра.

Слайд 11 4 Решение задач на догадку и перебор вариантов
Задача
В

4 Решение задач на догадку и перебор вариантовЗадачаВ ящике лежит много

ящике лежит много шариков трех цветов. Какое наименьшее количество

шариков надо вынуть из мешка наугад, чтобы наверняка оказалось хотя бы два шарика одного цвета?

Слайд 12 4 Решение задач на догадку и перебор вариантов
Варианты
1-й

4 Решение задач на догадку и перебор вариантовВарианты1-й вариант: вынуть 2

вариант: вынуть 2 шарика. Все они могут быть и

одного и разного цвета.
2-й вариант: вынуть 3 шарика. Все они могут быть и одного и разного цвета.
3-й вариант: вынуть 4 шарика. Обязательно 2 из них будут одного цвета.

Слайд 13 5 Метод фишек (метод линейного упорядочивания элементов множеств)
Задача
В

5 Метод фишек (метод линейного упорядочивания элементов множеств)ЗадачаВ очереди за билетами

очереди за билетами в кино стоят 4 мальчика: Юра,

Миша, Володя, Олег. Известно, что Юра купит билет раньше Миши, но позже Олега. Володя не стоит рядом ни с Олегом, ни с Юрой. Кто за кем стоит?

Слайд 14 5 Метод фишек (метод линейного упорядочивания элементов множеств)
Решение
Ю

М
О Ю М
В О В Ю В М
О Ю

М В

Слайд 15 6 Методы решения задач на разрезания и распилы
Правила,

6 Методы решения задач на разрезания и распилыПравила, которые необходимо знать:

которые необходимо знать:
количество кусков при разрезании на одно

больше количества пилов и резов;
количество пилов на одно меньше числа кусков;
число кусков при разрезании «тортов» или «бубликов» через их центр в 2 раза больше числа резов;
следует уточнить, проходят ли все резы через одну точку

Слайд 16 6 Методы решения задач на разрезания и распилы
Задача
Портной

6 Методы решения задач на разрезания и распилыЗадачаПортной имеет кусок сукна

имеет кусок сукна длиной 12 метров. Каждый день он

отрезает по 2 метра ткани. По истечении скольких дней портной отрежет последний кусок?

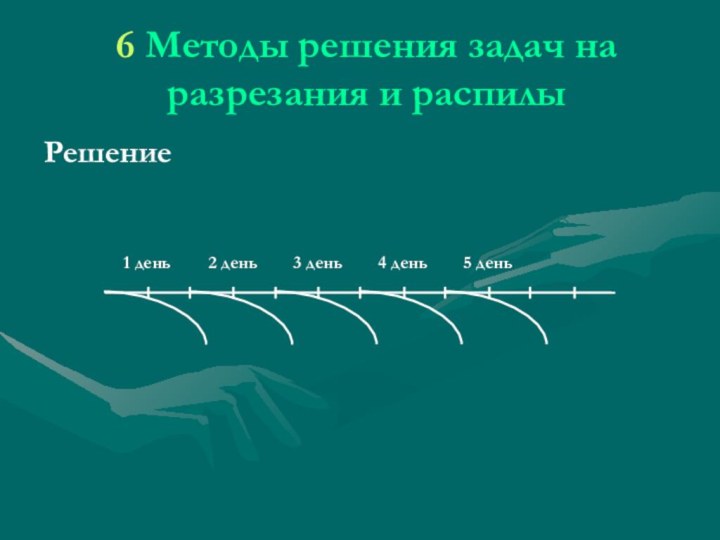
Слайд 17 6 Методы решения задач на разрезания и распилы
1

день
2 день
3 день
4 день
5 день
Решение

Слайд 18 6 Методы решения задач на разрезания и распилы
Задача
На

6 Методы решения задач на разрезания и распилыЗадачаНа какое максимальное число

какое максимальное число кусков можно разделить круглый блинчик при

помощи трех прямолинейных разрезов, не проходящих через одну точку?

Слайд 19 6 Методы решения задач на разрезания и распилы

Решение

Слайд 20 7 Задачи на умение рассуждать
Задача
Мама хочет поджарить на

7 Задачи на умение рассуждатьЗадачаМама хочет поджарить на завтрак дочке 3

завтрак дочке 3 гренки. На сковородку помещаются только 2

гренки. На поджаривание с одной стороны требуется одна минута. Мама очень спешит.
Поджаривать надо с обеих сторон. Сколько на это уйдет времени?

Слайд 21 7 Задачи на умение рассуждать
Решение
Наименьшее количество времени уйдет,

7 Задачи на умение рассуждатьРешениеНаименьшее количество времени уйдет, если сначала положить

если сначала положить 1-ю и 2-ю гренки и жарить

минуту, потом 1-ю перевернуть, а 2-ю снять и заменить ее 3-ей. Жарить 2-ю минуту, потом 1-ю снять, так как она готова, перевернуть 3-ю и дожарить 2-ю. На это уйдет 3 минуты.

Слайд 22 8 Прием «Реши сначала частный случай»
Задача
Даны 2 одинаковых

8 Прием «Реши сначала частный случай»ЗадачаДаны 2 одинаковых стакана. В одном

стакана. В одном вино, в другом вода. Из стакана

с водой взяли одну чайную ложку воды и перелили в стакан с вином, размешали и из стакана с вином перелили обратно в стакан с водой тоже чайную ложку жидкости. Спрашивается, одинаковая или разная концентрация вина в воде или воды в вине установится?

Слайд 23 8 Прием «Реши сначала частный случай»
Решение
Ответ не зависит

8 Прием «Реши сначала частный случай»РешениеОтвет не зависит от количества перелитых

от количества перелитых жидкостей, поэтому решим частный случай. Пусть

в стаканах по 200 граммов жидкости. Переливаем в вино 100 г воды. Концентрация воды в вине будет 100/(100+200)=0,3333. Затем переливаем 100г разбавленного вина в стакан с водой. В этих 100г будет 33,333г воды и 66,666г вина. Поэтому концентрация вина в воде оказалась 66,666/200=0,3333