Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Как учились математике дети в прошлые времена

Содержание

2. Введение Мне стало интересно: как учились дети
3. Цели и задачиПолучить ответ на вопрос: «Легче
4. Древний Египет
5. Цифры Древнего Египта
6. Школы древнего ЕгиптаПервые школы в Древнем Египте
7. Задачи на папирусахУровень древнеегипетской математики был довольно
8. А теперь попробуем решить древнеегипетскую задачу В
9. Решение:7*7*7*7*7==16807Ответ: вырастет 16807 мер зерна.
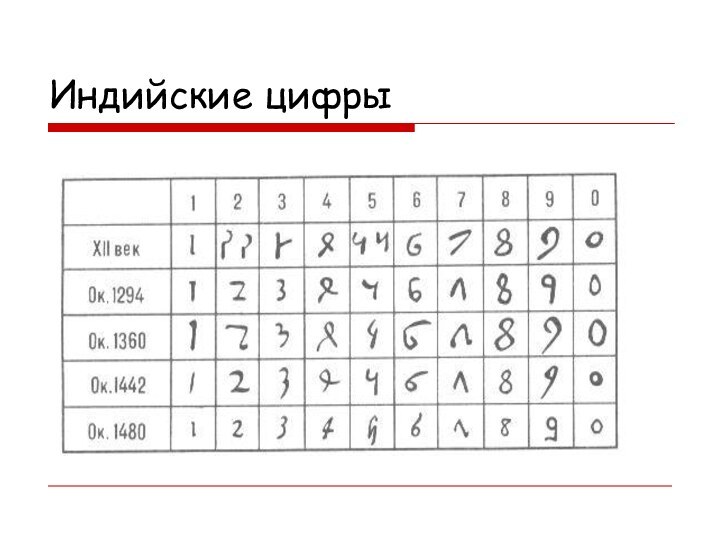
10. Древняя Индия
11. Индийские цифры
12. Цифра нольДревнеиндийские математики во 2 веке нашей
13. Школы в древней ИндииВ Древней Индии обучение
14. Попробуйте решить древнеиндийскую задачуИз четырех жертвователей
15. Решение:Пусть x монет дал первый. 1- х2-
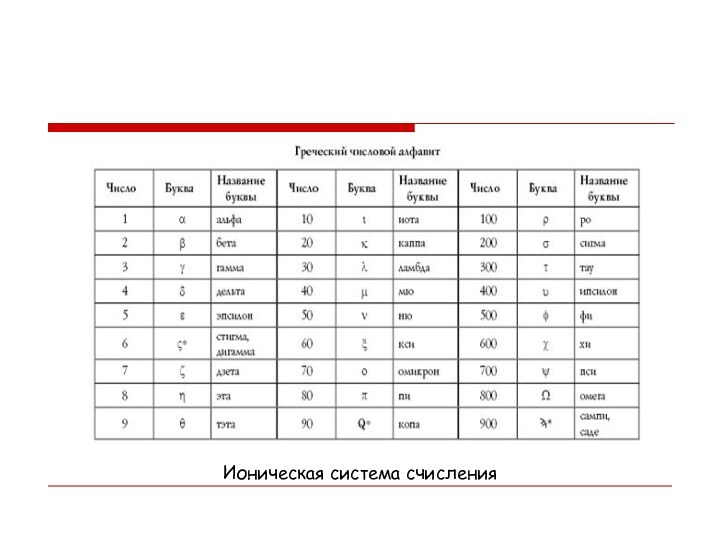
16. Древняя Греция
17. Аттические обозначения чиселЦифры Древней Греции
18. Ионическая система счисления
19. Математические школы древней ГрецииВ древней Греции в
20. Задача Герона Александрийского Стебель лотосаНа поверхности озера,посещаемого
21. Решение Длина стебля лотоса 2 локтя, если
22. Древняя Русь
23. Славянские цифры
24. Обучение на Руси до XVIII в. Обучение
25. В XVIII веке появились светские школы и
26. Задача из «Арифметики» МагницкогоВ жаркий день 6
27. Решение: Дано:За 8 час. – 6 чел.За
28. ВыводыМое исследование показало, что учится было с
29. Список использованной литературы: Большая биографическая энциклопедия, 2009
30. Скачать презентацию
31. Похожие презентации

Введение Мне стало интересно: как учились дети математике в прошлом. Какие они решали задачи? Смогу ли я их решить? Будет ли мне трудно это сделать или легко? Свое исследование я решила ограничить изучением самых известных древних

Главная
Математика
Как учились математике дети в прошлые времена

Как учились математике дети в прошлые временаПредметное исследованиеГулк ЕкатериныУченицы 5 аш класса

Введение Мне стало интересно: как учились дети математике в прошлом. Какие они

Цели и задачиПолучить ответ на вопрос: «Легче или тяжелее было учиться нашим

Школы древнего ЕгиптаПервые школы в Древнем Египте появляются в 3-ем тысячелетии до

Задачи на папирусахУровень древнеегипетской математики был довольно высок. Источников, по которым можно

А теперь попробуем решить древнеегипетскую задачу В доме 7 кошек, Каждая

Решение:7*7*7*7*7==16807Ответ: вырастет 16807 мер зерна.

Цифра нольДревнеиндийские математики во 2 веке нашей эры первые стали использовать знак

Школы в древней ИндииВ Древней Индии обучение носило семейно-школьный характер, причем роль

Попробуйте решить древнеиндийскую задачуИз четырех жертвователей второй дал вдвое больше первого.

Решение:Пусть x монет дал первый. 1- х2- 2х3- 6х4- 24хтогда х+2х+6х+24х=13233х=132х=132:33х=4Ответ: первый

Аттические обозначения чиселЦифры Древней Греции

Математические школы древней ГрецииВ древней Греции в Александрии Евклид в 325 году

Задача Герона Александрийского Стебель лотосаНа поверхности озера,посещаемого стаями фламинго и журавлей, плавает

Решение Длина стебля лотоса 2 локтя, если он поднимался над водой на

Обучение на Руси до XVIII в. Обучение грамоте начиналось при достижении ребенком

В XVIII веке появились светские школы и новые учебники«Букварь» Ф.Поликарпова, «Юности честное

Задача из «Арифметики» МагницкогоВ жаркий день 6 косцов выпили бочонок кваса за

Решение: Дано:За 8 час. – 6 чел.За 3 час. - ? чел.Пусть

ВыводыМое исследование показало, что учится было с одной стороны тяжелее , так

Список использованной литературы: Большая биографическая энциклопедия, 2009 А.Н.Джуринский «История педагогики и образования»,

Слайды презентации

Слайд 2 Введение
Мне стало интересно: как учились дети математике

Введение Мне стало интересно: как учились дети математике в прошлом. Какие

в прошлом. Какие они решали задачи? Смогу ли я

их решить? Будет ли мне трудно это сделать или легко? Свое исследование я решила ограничить изучением самых известных древних цивилизаций, а так же остановиться подробнее на истории нашей страны.

Слайд 3 Цели и задачи
Получить ответ на вопрос: «Легче или

Цели и задачиПолучить ответ на вопрос: «Легче или тяжелее было учиться

тяжелее было учиться нашим предкам?»
Какими системами счисления они пользовались?
Где

и как учились?

Слайд 4 Древний Египет

Слайд 5 Цифры Древнего Египта

Слайд 6 Школы древнего Египта
Первые школы в Древнем Египте появляются

Школы древнего ЕгиптаПервые школы в Древнем Египте появляются в 3-ем тысячелетии

в 3-ем тысячелетии до н. э. Они были небольшими

по числу учеников, за обучение в них взималась высокая плата. Школу посещали в основном мальчики из семей чиновников, жрецов, землевладельцев, зажиточных граждан, девочки чаще обучались дома. Обучение было индивидуальным, его продолжительность зависела от старания и способностей ученика.

Слайд 7 Задачи на папирусах
Уровень древнеегипетской математики был довольно высок.

Задачи на папирусахУровень древнеегипетской математики был довольно высок. Источников, по которым

Источников, по которым можно судить об этом три. Папирус

Райнда, Московский папирус и «Кожаный свиток египетской математики». В папирусах есть задачи на вычисление- образцы выполнения арифметических операций, задачи на раздел имущества, на нахождение объёма амбара или корзины, площади поля.

Слайд 8 А теперь попробуем решить древнеегипетскую задачу
В доме

7 кошек, Каждая кошка съедает 7 мышей, каждая мышь съедает 7

колосьев, каждый колос даёт 7 растений, на каждом растении вырастает 7 мер зерна. Сколько мер зерна вырастет из растений ?

Слайд 9 Решение:
77777=
=16807
Ответ: вырастет 16807 мер зерна.

Слайд 10 Древняя Индия

Слайд 11 Индийские цифры

Слайд 12 Цифра ноль
Древнеиндийские математики во 2 веке нашей эры

Цифра нольДревнеиндийские математики во 2 веке нашей эры первые стали использовать

первые стали использовать знак 0,
называемый по-индийски «сунья», что дословно

означает «ничто». Интересно заметить, что в первоначальном начертании нуль изображался точкой и лишь спустя много веков – в виде маленького кружка.

Слайд 13 Школы в древней Индии
В Древней Индии обучение носило

Школы в древней ИндииВ Древней Индии обучение носило семейно-школьный характер, причем

семейно-школьный характер, причем роль семьи была доминирующей. В период

индуизма воспитание и обучение в Древней Индии основывалось на идее, согласно которой каждый человек должен развивать свои качества, чтобы органично вписаться в свою касту. Брахманов (жрецов), кшатриев (воинов), вайшьев (крестьян) или шудры (слуг).

Слайд 14 Попробуйте решить древнеиндийскую задачу
Из четырех жертвователей второй дал

вдвое больше первого.
Третий дал втрое больше второго.
Четвертый

вчетверо больше третьего, а все вместе они дали 132 монеты. Сколько монет дал первый?

Слайд 15 Решение:
Пусть x монет дал первый.
1- х
2- 2х
3-

Решение:Пусть x монет дал первый. 1- х2- 2х3- 6х4- 24хтогда х+2х+6х+24х=13233х=132х=132:33х=4Ответ:

6х
4- 24х
тогда х+2х+6х+24х=132
33х=132
х=132:33
х=4
Ответ: первый жертвователь дал 4 монеты.

Слайд 16 Древняя Греция

Слайд 17 Аттические обозначения чисел
Цифры Древней Греции

Слайд 18 Ионическая система счисления

Слайд 19 Математические школы древней Греции
В древней Греции в Александрии

Математические школы древней ГрецииВ древней Греции в Александрии Евклид в 325

Евклид в 325 году до нашей эры
основал известнейшую

древнюю
математическую школу

Слайд 20 Задача Герона Александрийского Стебель лотоса

На поверхности озера,
посещаемого стаями

Задача Герона Александрийского Стебель лотосаНа поверхности озера,посещаемого стаями фламинго и журавлей,

фламинго и
журавлей, плавает лотос, стебель
которого на пол-локтя

поднимается над водой. Гонимый
ветром, стебель постепенно
наклоняется, погружается в воду
и, в конце концов, совсем исчезает
под водой и касается дна на
расстоянии двух
локтей от того места, где и вырос.
Подсчитай, о мудрый математик,
глубину озера.

Слайд 21 Решение
Длина стебля лотоса 2 локтя, если он

Решение Длина стебля лотоса 2 локтя, если он поднимался над водой

поднимался над водой на 0,5 стебля то,
2-0,5=1,5(лок.)
Ответ: глубина озера

– полтора локтя.

Слайд 22 Древняя Русь

Слайд 23 Славянские цифры

Слайд 24 Обучение на Руси до XVIII в.
Обучение грамоте

Обучение на Руси до XVIII в. Обучение грамоте начиналось при достижении

начиналось при достижении ребенком 7-летнего возраста Училища (начальные школы)

организовывались при церквях домах священников и дьяков. Позже с изобретением книгопечатанья дети стали учиться по печатным учебникам.

Слайд 25 В XVIII веке появились светские школы и новые

В XVIII веке появились светские школы и новые учебники«Букварь» Ф.Поликарпова, «Юности

учебники
«Букварь» Ф.Поликарпова, «Юности честное зерцало» «Первое поучение отрокам» Ф.

Прокоповича , «Арифметика» составленная Л.Ф. Магницким.
Учебник Магницкого был первым русским учебником математики. Он был издан в 1703 году и оставался основным учебником по математике до конца XVIII века. И по сей день это самый известный математический учебник в нашей стране.

Слайд 26 Задача из «Арифметики» Магницкого

В жаркий день 6 косцов

Задача из «Арифметики» МагницкогоВ жаркий день 6 косцов выпили бочонок кваса

выпили бочонок кваса за 8 часов. Нужно узнать, сколько

косцов за 3 часа выпьют такой же бочонок кваса?

Слайд 27 Решение:
Дано:
За 8 час. – 6 чел.
За 3

Решение: Дано:За 8 час. – 6 чел.За 3 час. - ?

час. - ? чел.
Пусть X чел. за 3 час.

X*3 =6*8
X*3=48
X=3:48
X=16
Ответ: за 3 часа
бочонок кваса
выпьют 16 косцов.

Слайд 28 Выводы
Мое исследование показало, что учится было с одной

ВыводыМое исследование показало, что учится было с одной стороны тяжелее ,

стороны тяжелее , так как использовались более сложные системы

счисления, методы обучения были не очень гуманными. Моим сверстникам было не просто, да и не все из них могли позволить себе учебу. Тем не менее задачи мне понравились решать их было интересно. Вот бы и в наших учебниках было по больше задач на развитие логики.

Слайд 29 Список использованной литературы:
Большая биографическая энциклопедия, 2009 А.Н.Джуринский «История

Список использованной литературы: Большая биографическая энциклопедия, 2009 А.Н.Джуринский «История педагогики и

педагогики и образования», М.:Из-во Юрайт, 2011
Мазалова М.А., Уракова Т.В.

История педагогики и образования: Конспект лекций. - М.: Высшее образование, 2006
Я.И.Перельман «Занимательна арифметика», М.: АСТ: Астрель, 2011
Шикман А. П. Деятели отечественной истории. Биографический справочник. М., 1997
Интернет-ресурсы