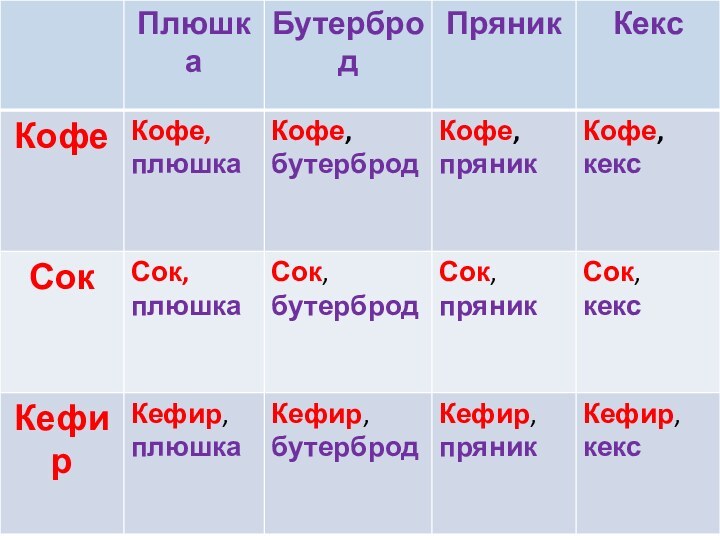
или кекс, а запить их он может кофе, соком
или кефиром. Из скольких вариантов завтрака Вова может выбирать? Пример 1.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть




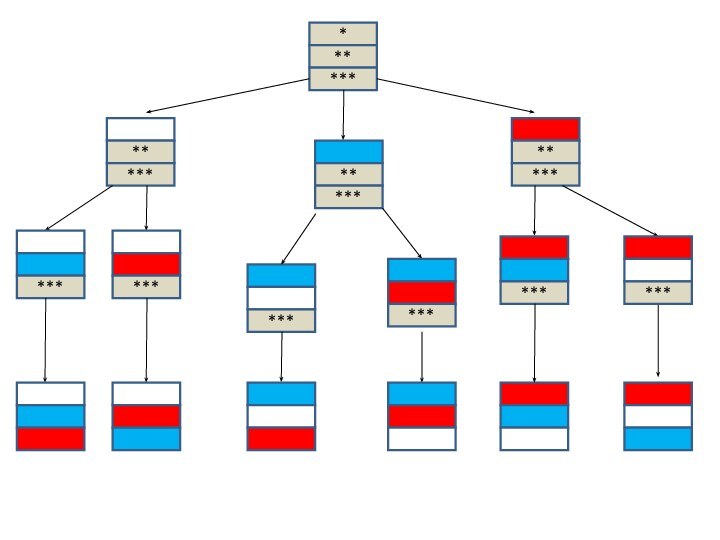

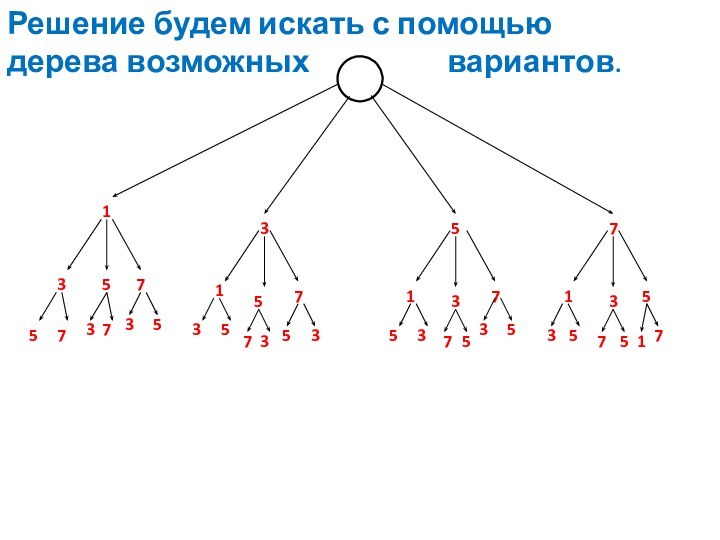




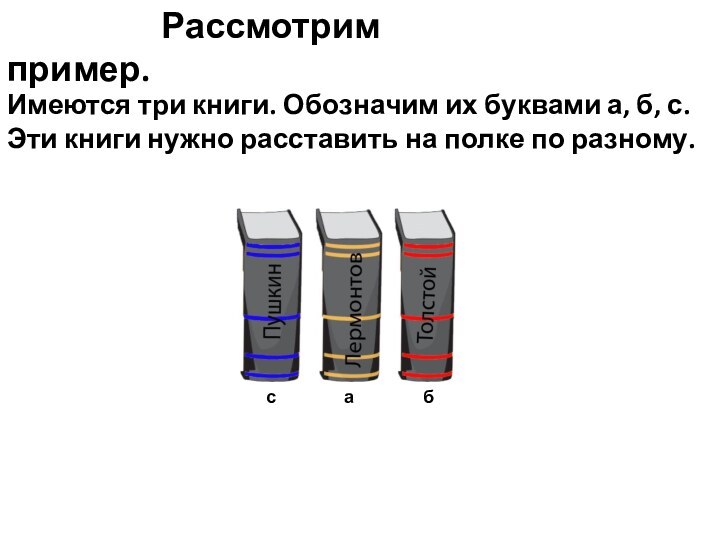







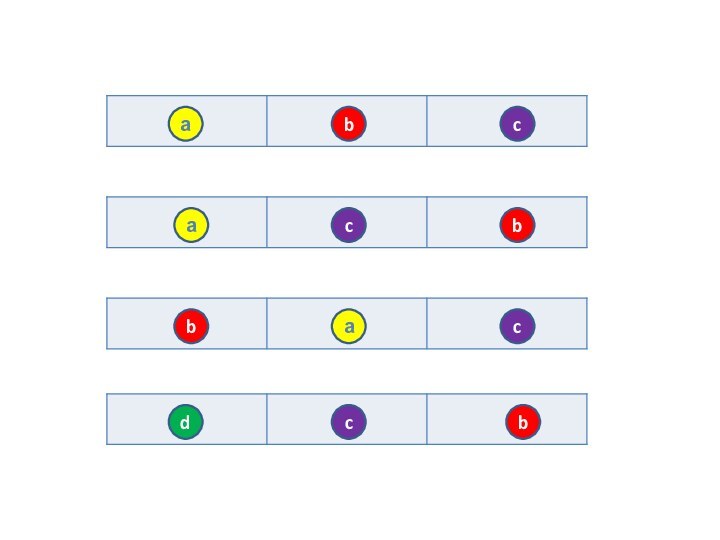


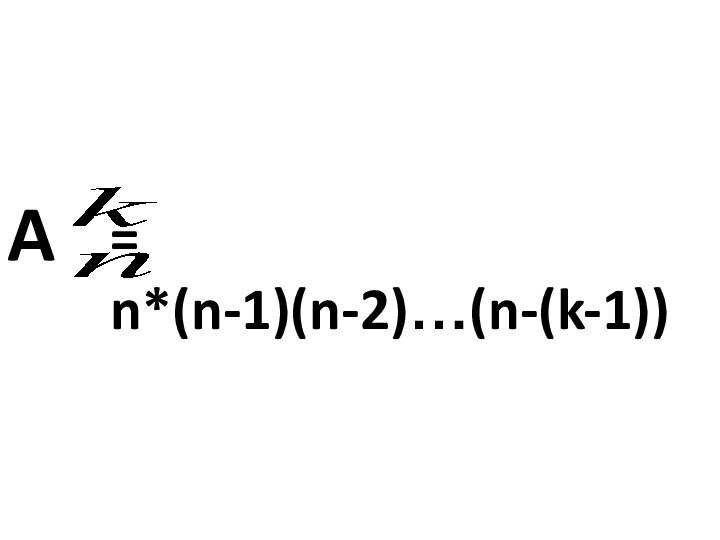
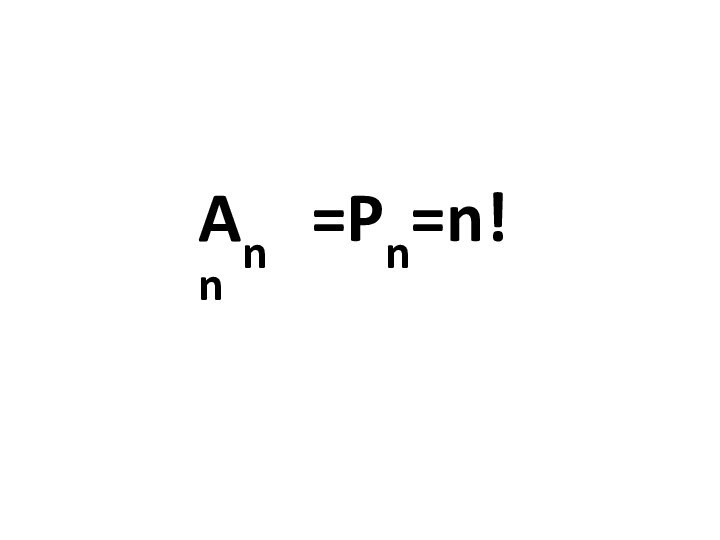


















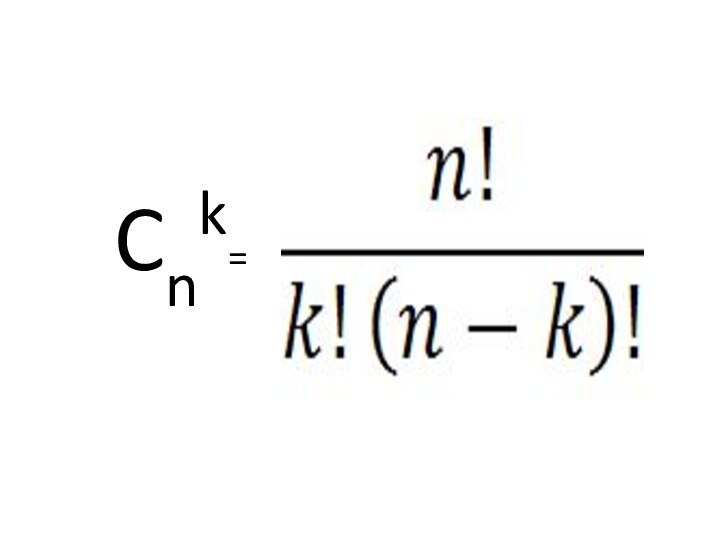






Пример 1.
а
б
с
б
с
а
с
а
б
с
б
а
Сколько различных четырехзначных чисел, в которых цифры не повторяются, можно составить из чисел 0,2,4,6?
Имеются девять различных книг, четыре из которых учебники. Сколькими способами можно расставить эти книги на полке так, чтобы все учебники стояли рядом?
В расписании на понедельник шесть уроков : алгебра, геометрия, биология, история, физкультура, химия.
Сколькими способами можно составить расписание уроков на этот день так, чтобы два урока математики стояли рядом.
A
Учащиеся второго класса изучают 8 предметов. Сколькими способами можно составить расписание
на один день, чтобы в нем было 4 различных предмета?
На странице альбома 6 свободных мест для фотографий. Сколько существует способов размещения фотографий в свободные места?
a) 4 фотографии;
b) 6 фотографий.
Сколько трехзначных чисел ( без повторения цифр в записи числа) можно составить из цифр
0, 1, 2, 3, 4, 5, и 6?
Из трехзначных чисел, записанных с помощью цифр
1, 2, 3, 4,5, 6, 7, 8, 9 (без повторений цифр).
Сколько таких в которых:
a) не встречаются цифры 6 и 7;
b) цифра 8 является последней?
Сколько существует семизначных телефонных номеров,
в которых все цифры различные и первая цифра отличается от 0?
Из 15-ти членов туристической группу надо выбрать трех дежурных.
Сколькими способами можно сделать этот выбор?
Из вазы с фруктами, где лежит 9 яблок и 6 груш,
нужно выбрать 3 яблока и 2 груши.
Сколькими способами это можно сделать?
В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в олимпиаде?
В лаборатории, в которой работают заведующий и
10 сотрудников, надо отправить в командировку 5 человек.
Сколькими способами это можно сделать если,
a)заведующий лаборатории должен ехать
b) заведующий должен остаться.
В классе учатся 16 мальчиков и 12 девочек.
Для уборки территории нужно выделить 4 мальчиков и 3 девочек.
Сколькими способами это можно сделать?