- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Комбинаторные задачи 5 класс
Содержание
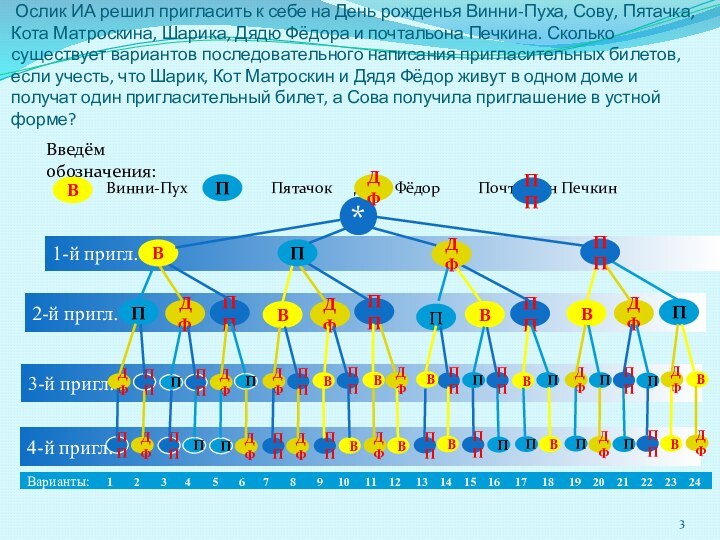
- 2. Ослик ИА решил пригласить к себе на
- 3. 2-й пригл.3-й пригл.ВДФПППДФППВППППВДФДФППДФПППВПДФППДФППДФППППДФППВВВППППВП Ослик ИА решил пригласить
- 4. Первыми пришли Винни-Пух, Пятачок и Сова. Подойдя
- 5. Первыми пришли Винни-Пух, Пятачок и Сова. Подойдя
- 6. А если бы трехзначный шифр состоял из
- 7. Подождав некоторое время остальных гостей Ослик предложил
- 8. Друзья ответили, что Тр-тр Митя сломался и
- 9. Ослик, ожидая гостей, приготовил на обед борщ,
- 10. Перед тем, как подарить подарки (Пятачок принес
- 11. Перед отъездом почтальон Печкин должен успеть
- 12. Подоспели новые гости. Заходят в дом и
- 13. Сколько способов размещения друзей за столом возможны
- 14. Вкусно покушав, весёлая компания стала играть в
- 15. После танцев гости решили оставить на память
- 16. Мудрая Сова предложила написать ещё одно предложение:
- 17. Уже стемнело, а гостям не хочется расходиться
- 18. Всех гостей Ослик ИА решил развести по
- 19. Скачать презентацию
- 20. Похожие презентации


















Слайд 3
2-й пригл.
3-й пригл.
В
ДФ
П
ПП
ДФ
ПП
В
ПП
ПП
В
ДФ
ДФ
ПП
ДФ
П
ПП
В
П
ДФ
ПП
ДФ
ПП
ДФ
П
ПП
П
ДФ
ПП
В
В
В
П
П
ПП
В
П
Ослик ИА решил пригласить к
себе на День рожденья Винни-Пуха, Сову, Пятачка, Кота Матроскина,
Шарика, Дядю Фёдора и почтальона Печкина. Сколько существует вариантов последовательного написания пригласительных билетов, если учесть, что Шарик, Кот Матроскин и Дядя Фёдор живут в одном доме и получат один пригласительный билет, а Сова получила приглашение в устной форме?
Винни-Пух Пятачок Дядя Фёдор Почтальон Печкин
1-й пригл.
В
ДФ
П
ПП
В
П
ДФ
ПП
4-й пригл.
ДФ
ПП
ДФ
П
ПП
В
П
ДФ
ПП
ДФ
ПП
ДФ
П
ПП
П
ДФ
ПП
В
В
В
П
П
ПП
В
Варианты: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
*
Введём обозначения:
П
Слайд 4 Первыми пришли Винни-Пух, Пятачок и Сова. Подойдя к
двери и увидев кодовый замок, они поняли, что забыли
код. Подумав, Пятачок вспомнил, что код-трёхзначное число, а мудрая Сова знала, что оно состоит из трёх цифр 1, 2, 3. Сколько всевозможных вариантов им придётся перебрать, чтобы попасть в гости?Слайд 5 Первыми пришли Винни-Пух, Пятачок и Сова. Подойдя к
двери и увидев кодовый замок, они поняли, что забыли
код. Подумав, Пятачок вспомнил, что код-трёхзначное число, а мудрая Сова знала, что оно состоит из трёх цифр 1, 2, 3. Сколько всевозможных вариантов им придётся перебрать, чтобы попасть в гости?
Решение:
Первая цифра может быть выбрана из любых трех цифр (1,2,3)
Для каждой второй цифры существует выбор тоже из трёх цифр
(1, 2, 3).
Для каждой третьей цифры опять выбор из трёх цифр, так как
в задании не оговорено, что цифры повторяться не должны.
Значит, 3×3×3=27.
Ответ: 27
Слайд 6 А если бы трехзначный шифр состоял из цифр
1, 2, 3, но без их повторений? Сколькими способами
замок мог быть закодирован в этом случае? Решение:
1
2
3
2
3
3
2
1
3
3
1
1
2
2
1
По правилу произведения получаем:
3×2×2=12
Ответ: 12 способами.
Слайд 7 Подождав некоторое время остальных гостей Ослик предложил Сове
позвонить друзьям, но из семизначного телефонного номера он помнил
только первые три цифры 295. Сколько всего вариантов телефонных номеров можно составить, чтобы помочь Ослику дозвониться до своих друзей? Решение:
295 * * * *
На четвёртом месте может стоять любая из 10 цифр: 0,1,2…9.
На пятом, шестом, седьмом местах также могут стоять любые из 10-ти цифр.
Значит, различных вариантов будет 10×10×10×10=10000
Ответ:10000 вариантов.
Слайд 8 Друзья ответили, что Тр-тр Митя сломался и пока
они приехать не могут. Приносят свои извинения и предлагают
не ждать их, а садиться за стол. Сколькими способами Ослик ИА может разместить за столом трёх гостей? Решение:
По правилу произведения
получаем:
3×2×1=6(способов).
Ответ: 6 способами Ослик ИА может разместить за столом 3 гостей.
.
Слайд 9 Ослик, ожидая гостей, приготовил на обед борщ, вермишелевый
суп, три вторых блюда и пять напитков. Сколькими способами
гости могут выбрать себе обед, состоящий из первого, второго и третьего блюд? Решение:
Первое блюдо может быть выбрано двумя способами.
Второе блюдо - тремя способами.
Третье блюдо - пятью способами.
По правилу произведения получаем:
2×3×5=30(способов)
Ответ: 30 способов.
Слайд 10 Перед тем, как подарить подарки (Пятачок принес лопнувший
шарик, Винни-Пух пустой горшочек, Сова-хвост), гости решили поменять их
между собой. Сколько существует возможных вариантов обмена подарками, если каждый приглашенный не должен остаться со своим подарком? Решение:
Введём обозначение: Винни – Пух – В, Сова – С, Пятачок – П.
Обмен может произойти следующим образом:
В-С-П-В
В-П-С-В
С-П-В-С
С-В-П-С
П-В-С-П
П-С-В-П
Так как последние два
варианта являются повторением
третьего и четвёртого, то
6-2=4(варианта).
Ответ: 4 варианта.
Слайд 11 Перед отъездом почтальон Печкин должен успеть разнести
письма в 7 различных учреждений. Сколько маршрутов для него
существует? Решение:
По правилу произведения получаем:
7×6×5×4×3×2×1=5040 (способов)
Ответ: 5040 способов.
Слайд 12 Подоспели новые гости. Заходят в дом и начинают
обмениваться рукопожатиями. Сколько всего произойдёт рукопожатий?
Решение:
Каждый из присутствующих в
домездоровается с четырьмя гостями.
Поэтому:
4×4=16(рукопожатий)
Ответ: 16 рукопожатий.
Слайд 13 Сколько способов размещения друзей за столом возможны сейчас,
когда в доме присутствуют 7 гостей и Ослик?
Решение:
По
правилу произведения получаем:8×7×6×5×4×3×2×1=
=40320(способов)
Ответ: 40320 способов размещения 8 друзей за столом существует.
Слайд 14 Вкусно покушав, весёлая компания стала играть в игру
с разноцветными треугольниками. Имеется 4 треугольника - синий, жёлтый,
зелёный, красный. Сколько можно составить ёлочек из предложенных треугольников, не повторяя цвета, используя для составления каждой ёлочки все 4 треугольника? Решение:
Воспользуемся правилом произведения:
4×3×2×1=24 (способа)
Ответ: 24 различных ёлочки можно составить.
Слайд 15 После танцев гости решили оставить на память Ослику
поздравительное послание, состоящее из одного предложения, в котором присутствуют
слова: «Поздравляем мы тебя!» Сколько различных способов написания этого предложения существует? Сможет ли каждый из гостей составить своё предложение? Решение:
По правилу произведения получаем:
3×2×1=6 (способов)
Ответ: существует 6 различных способов написания данного предложения. Каждый из гостей не сможет записать своё, отличное от других предложение.
Слайд 16 Мудрая Сова предложила написать ещё одно предложение: «Тебя
мы очень любим!» Сколько в этом случае вариантов данного
предложения существует? Решение:
4×3×2×1=24(варианта)
Ответ: предложение, состоящее из 4 слов,
можно составить 24 способами.
Слайд 17 Уже стемнело, а гостям не хочется расходиться по
домам. Ослик предложил поиграть в шашки. Сколько партий будет
сыграно если предположить, что каждый из гостей будет играть друг с другом? Решение:
Каждый игрок должен сыграть по 7 партий. Рассмотрим случаи, когда игроки не повторяются. Первый должен сыграть 7 партий (со 2, 3, 4, 5, 6, 7, 8), второй- 6 партий (с 3, 4, 5,6, 7, 8), третий – 5 партий (с 4, 5, 6, 7, 8), четвёртый – 4 партии (с 5, 6, 7,8), пятый – 3 партии (с 6, 7, 8), шестой – 2 партии (с 7, 8), седьмой – 1 партия (с 8). Отсюда, количество партий:
7+6+5+4+3+2+1=28.
Ответ: 28 партий.
Слайд 18 Всех гостей Ослик ИА решил развести по домам
сам. Сколько возможных вариантов развоза гостей домой существует, если
учесть, что Кот Матроскин, Шарик и Дядя Фёдор живут в одном доме? Решение:
5×4×3×2×1=120 (вариантов)развоза гостей существует.
Ответ: 120 возможных вариантов развоза гостей существует.





























