- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Квадратный трехчлен. Квадратичная функция. Квадратные уравнения. Разложение квадратного трехчлена на множители
Содержание
- 2. Разработано учителем математики МОУ «СОШ» п. Аджером Корткеросского района Республики Коми Мишариной Альбиной Геннадьевной
- 3. СодержаниеКвадратный трехчленКвадратичная функцияКвадратные уравненияРазложение квадратного трёхчлена на множители
- 4. КВАДРАТНЫЙ ТРЕХЧЛЕН
- 5. ОпределениеМногочлен ax²+bx+c , где а, в,
- 6. Назовите коэффициенты:1) 2х² - 6х + 12)
- 7. КВАДРАТИЧНАЯ ФУНКЦИЯ
- 8. ЗапомнимФункция у = ax²+bx+c, где а, в,
- 9. Ветви параболы у = ax²+bx+c направлены вверх,
- 10. Найти координаты вершины параболы, её ось симметрии
- 11. Самостоятельно: вычислить координаты
- 12. Рефлексия: 1) Сегодня на уроке я
- 13. Квадратные уравнения
- 14. Содержание:Определение квадратного уравненияКлассификация квадратных уравненийСпособы решения квадратного уравнения
- 15. Определение Квадратным уравнением называется уравнение вида ax²+bx+c=0,
- 16. Классификация .
- 17. Запомним Решить квадратное уравнение – это значит
- 18. Способы решения квадратного уравнения:Разложением на множителиВыделением полного
- 19. Разложение левой части на множители
- 20. Например:Выделение полного квадрата
- 21. Рассмотрим ещё одно решение:Решим уравнение:
- 22. Алгоритм решения квадратного уравнения ПО ФОРМУЛЕ КОРНЕЙ:Найти
- 23. - если D=0, то данное
- 24. Решить уравнение: 2x2- 5x + 2 = 0Здесь a = 2, b = -5,
- 25. Решить самостоятельно:x2- 2x + 1 = 0.2x2-
- 26. Работаем в парах:1) Выберите квадратные уравнения и
- 27. Проверим:Квадратные уравнения: А) 2х²
- 28. Проверим:2) Приведенные квадратные уравнения:
- 29. Пример решения квадратного уравненияДано уравнение:Решение:
- 30. Самостоятельная работа (по вариантам)
- 31. Проверь решение:
- 32. Проверь решение:
- 33. Запомни: по теореме Виета решаются только приведенные
- 34. НАПРИМЕРДано приведённое квадратное уравнение
- 35. Решить : Решаем вместе:1) х² -
- 36. Проверим ответы:1) х₁ =-1 х₂
- 37. Решение квадратных уравнений по коэффициентам Если
- 38. Решить самостоятельно по группам:
- 39. Проверим:
- 40. Проверим:
- 41. Проверим:
- 42. Решим графически уравнение: Решение:преобразуемПусть у₁ =
- 43. Решить графически уравнения по вариантам: 1
- 44. Введение новой переменнойУмение удачно ввести новую переменную
- 45. Решить самостоятельно в парах: а) (х² -
- 46. Разложение квадратного трехчлена на множители
- 47. Запомнить: Если квадратное уравнение ax²+bx+c=0имеет корни х₁
- 48. Разложите квадратный трехчлен на множители:
- 49. Проверим 1 вариант1) (х-8)(х-3)2) (х+3)(х+4)3) – (х-1)(х+9)4)
- 50. Рефлексия: Сегодня на уроке я запомнил…Сегодня
- 51. СПАСИБО ЗА УРОК !!!
- 52. Скачать презентацию
- 53. Похожие презентации


















































Слайд 3
Содержание
Квадратный трехчлен
Квадратичная функция
Квадратные уравнения
Разложение квадратного трёхчлена на множители
Слайд 5
Определение
Многочлен ax²+bx+c , где а, в, с
– числа (коэффициенты), причем
а ≠ 0
называется квадратным трехчленом Причем: а – старший коэффициент,
в - второй коэффициент
с – свободный член
Слайд 6
Назовите коэффициенты:
1) 2х² - 6х + 1
2) -
2х² + 8х – 5
3) 3х² + 2х
х² -
4х + 7- х² - 8
6х² - х - 2
а =2; в = -6; с = 1
2) а =-2; в = 8; с = -5
3) а =3; в = 2; с = 0
4) а =1; в = -4; с = 7
5) а =-1; в = 0; с = -8
6) а =6; в = -1; с = -2
Слайд 8
Запомним
Функция у = ax²+bx+c, где а, в, с
– произвольные числа, причем а ≠0 называется квадратичной.
Графиком квадратичной
функции является параболаСлайд 9 Ветви параболы у = ax²+bx+c направлены вверх, если
а > 0, и вниз если а < 0
Как
найти координаты вершины параболы? – абсцисса х₀ вершины параболы вычисляется по
формуле х₀ = - в/2а
- ордината у₀ вершины параболы
вычисляется подстановкой найденной х₀
в заданную функцию
Осью симметрии параболы является прямая
х = - в/2а
Запомним
Слайд 10 Найти координаты вершины параболы, её ось симметрии и
построить её:
у = 2х² - 8х + 1
у =
- 2х² +16х – 5Т.к. а =2 ; в =-8; с =1
то х₀ = 8 : (2·2)=2
у₀= 2·2² - 8·2 + 1=-7
Значит: (2; -7) координаты вершины, а ось симметрии параболы: х=2
2) Т.к. а=-2; в=16; с=-5
то х₀ = -16 : (2·(-2)) = 4
у₀ = -2· 4² + 16·4 - 5 = 27
Значит: (4; 27) координаты вершины; ось симметрии: х=4
Слайд 11 Самостоятельно: вычислить координаты
вершины параболы
1) у = х² + 4х + 5
2) у = 2х² + 4х
3) у = -3х² + 6х + 1
4) у = 3х² - 12х
5) у = х² + 6х - 2
6) у = -2х² + 8х - 5
7) у = -4х² - 8х
Проверим:
1) (-2; 1)
2) (-1; -2)
3) (1; 4)
4) (2; - 12)
5) (-3; - 11)
6) (2; 3)
7) (-1; 4)
Слайд 12
Рефлексия:
1) Сегодня на уроке я запомнил…
2) Сегодня
на уроке я научился…
3) Сегодня на уроке я
узнал … 4) Сегодня на уроке я выучил…
5) Сегодня на уроке было интересно …
6) Сегодня на уроке мне понравилось …
Слайд 14
Содержание:
Определение квадратного уравнения
Классификация квадратных уравнений
Способы решения квадратного уравнения
Слайд 15
Определение
Квадратным уравнением называется уравнение вида ax²+bx+c=0,
где x - переменная,
a, b,
c – любые действительные числа, причем a≠0. (Почему?)Причем: а – старший коэффициент
в - второй коэффициент
с – свободный член
Слайд 16
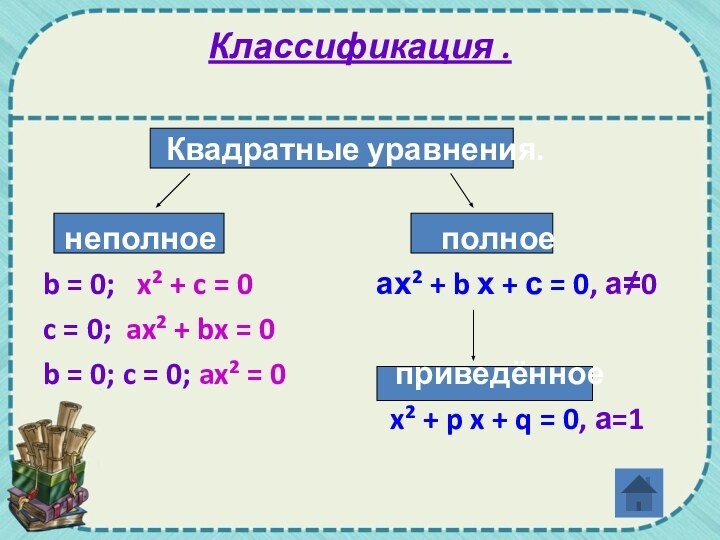
Классификация .
Квадратные уравнения.
неполное
полноеb = 0; x² + c = 0 ах² + b х + с = 0, а≠0
c = 0; ax² + bx = 0
b = 0; c = 0; ax² = 0 приведённое
x² + p x + q = 0, а=1
Слайд 17
Запомним
Решить квадратное уравнение – это значит найти
все его корни или установить, что их нет.
Причем: квадратное
уравнение может иметь либо 2 корня (если D >0), либо 1 корень (если D = 0),
либо вообще не иметь корней (если D <0)
Слайд 18
Способы решения квадратного уравнения:
Разложением на множители
Выделением полного квадрата
По
формуле корней (универсальный способ)
По теореме Виета
По коэффициентам
Графический
Введение новой переменной
Слайд 21
Рассмотрим ещё одно решение:
Решим уравнение: х²
+ 6х - 7 = 0.
Решение:
х² + 6х -7 = 0.х² + 2 · 3 · х + 9 – 9 – 7 = 0
(х² + 6х + 9) - 9 – 7 = 0
(х +3)² – 16 = 0.
(х +3)² = 16.
Значит: х +3 = 4 и х + 3 = -4.
х = 1 х =-7.
Ответ: 1; -7.
Слайд 22
Алгоритм решения квадратного уравнения ПО ФОРМУЛЕ КОРНЕЙ:
Найти число,
называемое дискриминантом квадратного уравнения
и
равное D = b²- 4ac. 2) Дискриминант показывает сколько корней имеет уравнение
- если D<0, то данное квадратное уравнение не имеет корней;
Слайд 23 - если D=0, то данное квадратное
уравнение имеет
единственный корень, который
равен
- если D>0, то данное квадратное уравнение
имеет два корня, которые равны
Слайд 24
Решить уравнение: 2x2- 5x + 2 = 0
Здесь a = 2, b = -5, c = 2.
Имеем D = b2- 4ac = (-5)2- 422 = 9.
Так как D > 0, то уравнение
имеет два корня.Найдем их по формуле
то есть x₁ = 2 и x₂ = 0,5 - корни заданного уравнения.
Слайд 25
Решить самостоятельно:
x2- 2x + 1 = 0.
2x2- 3x
+5= 0.
Проверим
1 уравнение:
получили один корень х = 1, т.к. D = 0Проверим
2 уравнение:
уравнение не имеет действительных корней, т.к. D < 0
Слайд 26
Работаем в парах:
1) Выберите квадратные уравнения и
определите
значения их коэффициентов:
А) 2х²
– 8 = 0; Б) -х² + 4х + 1 = 0;В) 3х³ + 2х – 9 = 0; Г) 5х – 3х² +2 = 0;
Д) х – 3 = 0; Е) 3 – 5х² – х = 0;
Ж) х² – х = 0. И) х² + 5 - 2х = 0
2) По коэффициентам указать приведенные
уравнения.
3) Из квадратных уравнений
выбрать неполные и решить их.
Слайд 27
Проверим:
Квадратные уравнения:
А) 2х² –
8 = 0, где а=2; в=0; с=-8
Б) -х² + 4х + 1 = 0, где а=-1; в=4; с=1
Г) 5х – 3х² + 2 = 0, где а=-3; в=5; с=2
Е) 3 – 5х² – х = 0, где а=-5; в=-1; с=3
Ж) х² – х = 0, где а=1; в=-1; с=0
И) х² + 5 - 2х = 0, где а=1; в=-2; с=5
Слайд 28
Проверим:
2) Приведенные квадратные уравнения:
И) х² + 5 - 2х = 0
3) Неполные квадратные уравнения:
А) 2х² – 8 = 0 и Ж) х² – х = 0
Решения: 2х² – 8 = 0 и х² – х = 0
2(х² - 4)=0 х(х-1)=0
2≠0; х² - 4 =0 х=0; х-1=0
х² = 4 х=0; х=1
х = ± 2
Слайд 33 Запомни: по теореме Виета решаются только приведенные квадратные
уравнения
Теорема Виета: Если корни х₁ и х₂ приведённого
квадратного уравнения х² + px + q = 0 , то х₁ + х₂ = - p, а х₁ · х₂ = q. Обратное утверждение: Если числа m и n таковы, что m + n = - p, m∙n = q, то эти числа являются корнями уравнения х² + px + q = 0.
Обобщённая теорема: Числа х₁ и х₂ являются корнями приведённого квадратного уравнения х² + px + q = 0 тогда и только тогда, когда х₁ + х₂ = - p, х₁ · х₂ = q.
Следствие: х² + px + q = (х – х₁)(х – х₂)
Слайд 34
НАПРИМЕР
Дано приведённое квадратное уравнение
x²-7x+10=0
Решение: методом подбора проверим числа
2 и 5. Их произведение равно 10 (т.е. свободному члену уравнения), а их сумма равна 7, (т.е. второму коэффициенту уравнения , но с противоположным знаком )
Значит эти числа и являются корнями данного уравнения.
Ответ: 2 и 5
Слайд 35
Решить :
Решаем вместе:
1) х² - 15х
+ 14 = 0
2) х² + 3х – 4
= 03) х² - 10х – 11 = 0
4) х² + 8х – 9 = 0
Решить
самостоятельно
в парах:
1) х² + 8х + 7 = 0
2) х² - 19х + 18 = 0
3) х² - 9х – 10 = 0
4) х² + 9х + 20 = 0
Слайд 37
Решение квадратных уравнений по коэффициентам
Если сумма коэффициентов равна
0, т.е. а + в + с = 0
, то х₁ = 1 х₂ = с/а.2) Если а –в + с = 0, то х₁ = -1 х₂ = -с/а.
3) Если а = с, в = а ² + 1, то
х₁ = –а = - с х₂ = -1/а = -1 /с.
4) Если а = с , в = - (а² + 1), то
х₁ = а = с х₂ = 1/а = 1/с
Слайд 38
Решить самостоятельно
по группам:
1) 3х² +
4х + 1 = 0,
2) 5х² - 4х – 9 = 0, 3) 6х² + 37х + 6 = 0,4) 7х² + 2х – 5 = 0,
5) 13х² - 18х + 5 = 0,
6) 5х² + х – 6 = 0,
7) 7х² - 50х + 7 = 0,
8) 6х² - 37х + 6 = 0,
9) 7х² + 50х + 7 = 0.
Слайд 42
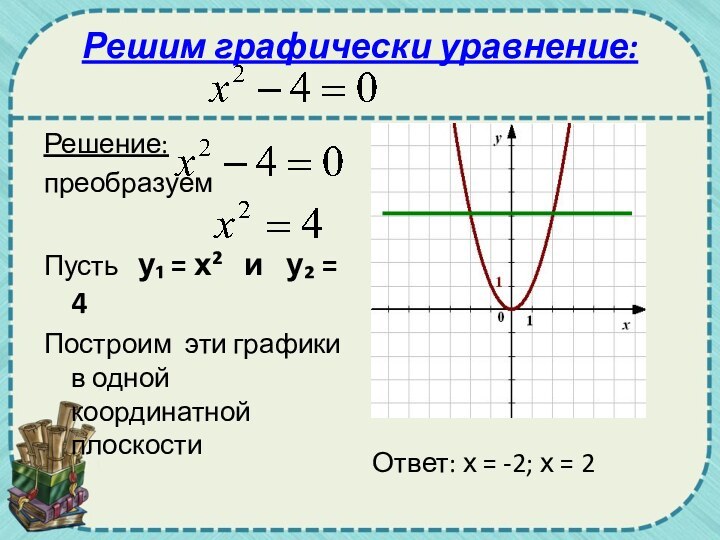
Решим графически уравнение:
Решение:
преобразуем
Пусть у₁ = х²
и у₂ = 4
Построим эти графики в
одной координатной плоскости
Ответ: х = -2; х = 2
Слайд 43
Решить графически уравнения
по вариантам:
1 вариант
1) х²
+ 2х – 3 = 0
2) - х² +
6х – 5 = 03) 2х² - 3х + 1 = 0
2 вариант
1) х² - 4х + 3 = 0
2) -х² - 3х + 4 = 0
3) 2х² - 5х + 2 = 0
Слайд 44
Введение новой переменной
Умение удачно ввести новую переменную –
облегчает решение
Например: надо решить уравнение (2х+3)² =
3(2х+3) – 2.Решение: пусть: а = 2х + 3.
Произведем замену переменной: а² = 3а - 2.
Тогда получим уравнение а² - 3а + 2 = 0 и у него D > 0.
Решим квадратное уравнение и получим: а₁ = 1, а₂ = 2.
Произведем обратную замену и вернемся к переменной х:
1). если а₁ = 1, то 2х + 3 = 1 и тогда х₁ = - 1;
2). если а₂ = 2, то 2х + 3 = 2 и тогда х₂ = - 0,5
Ответ: -1; -0,5.
Слайд 45
Решить самостоятельно в парах:
а) (х² - х)²
- 14(х² - х) + 24 = 0;
б)
(2х - 1)⁴ - (2х - 1)² - 12 = 0 Проверим ответы:
а)
б)
Слайд 47
Запомнить:
Если квадратное уравнение ax²+bx+c=0
имеет корни х₁ и
х₂, то квадратный трехчлен ax²+bx+c, раскладывается на множители следующим
образом:ax²+bx+c= а·(х - х₁)(х - х₂).
Слайд 48
Разложите квадратный трехчлен на множители:
1 вариант
1) х² - 11х + 24
2) х² +
7х + 12 3) - х² - 8х + 9
4) 3х² + 5х - 2
5) -5х² + 6х - 1
2 вариант
1) х² - 2х - 15
2) х² + 3х - 10
3) - х² + 5х - 6
4) 5х² + 2х - 3
5) -2х² + 9х - 4
Слайд 49
Проверим
1 вариант
1) (х-8)(х-3)
2) (х+3)(х+4)
3) – (х-1)(х+9)
4) 3·(х-1/6)(х+13/6)
5)
-5·(х-1)(х- 0,2)
2 вариант
1) (х-5)(х+3)
2) (х-2)(х+5)
3) - (х-2)(х-3)
4) 5·(х+1)(х-
0,6)5) -2·(х-½)(х-4)
Слайд 50
Рефлексия:
Сегодня на уроке я запомнил…
Сегодня на уроке
я научился…
Сегодня на уроке я узнал …
Сегодня
на уроке я выучил… Сегодня на уроке было интересно …
Сегодня на уроке мне понравилось …