- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Комбинации геометрических тел
Содержание
- 2. Цилиндр и призмаЦилиндр, описанный около призмыЦилиндр, вписанный в призму
- 3. Конус и пирамидаКонус, описанный около пирамидыКонус, вписанный в пирамидуR
- 4. Шар и цилиндр
- 5. Шар, описанный около цилиндраРадиус шара R,радиус цилиндра
- 6. Шар, вписанный в цилиндрРадиус шара R равен
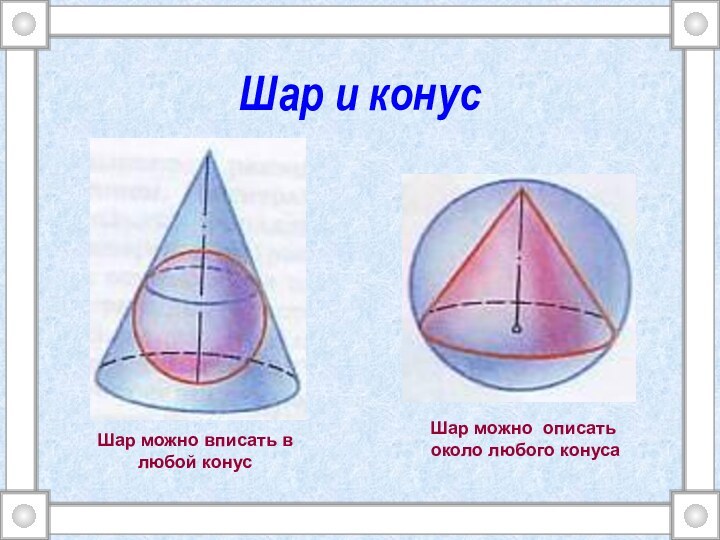
- 7. Шар и конусШар можно описать около любого конусаШар можно вписать в любой конус
- 8. Конус, вписанный в шар (шар, описанный около
- 9. Скачать презентацию
- 10. Похожие презентации
Цилиндр и призмаЦилиндр, описанный около призмыЦилиндр, вписанный в призму







Слайд 5
Шар, описанный около цилиндра
Радиус шара R,
радиус цилиндра r,
высота цилиндра H
связаны соотношением:
R2 =( )2 + r2.
Шар
можно описать около любого (прямого кругового) цилиндра.Окружности оснований цилиндра лежат на поверхности шара.
Центр шара лежит на середине высоты, проходящей через ось цилиндра.
Слайд 6
Шар, вписанный в цилиндр
Радиус шара R равен радиусу
цилиндра r, а диаметр шара равен высоте цилиндра:
R
= r 2R = HШар можно вписать только в такой цилиндр, высота которого равна диаметру основания
( такой цилиндр называется равносторонним)
Шар касается оснований в их центрах и боковой поверхности цилиндра по окружности большого круга шара, параллельной основаниям цилиндра
Слайд 8
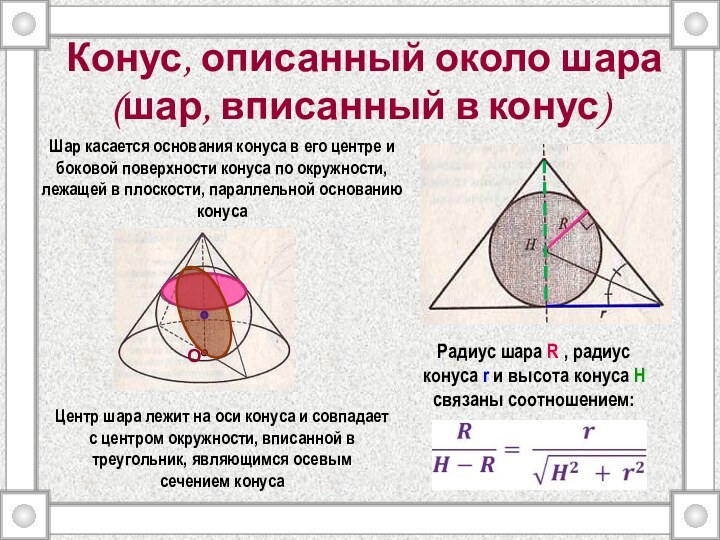
Конус, вписанный в шар
(шар, описанный около конуса)
Окружность основания
конуса и вершина конуса лежат на поверхности шара
Центр шара
лежит на оси конуса и совпадает с центром окружности, описанной около треугольника, являющегося осевым сечением конусаРадиус шара R, радиус конуса r и высота конуса H связаны соотношением:
R2= (H - R)2 + r2