Презентация на тему Понятие осевой симметрии

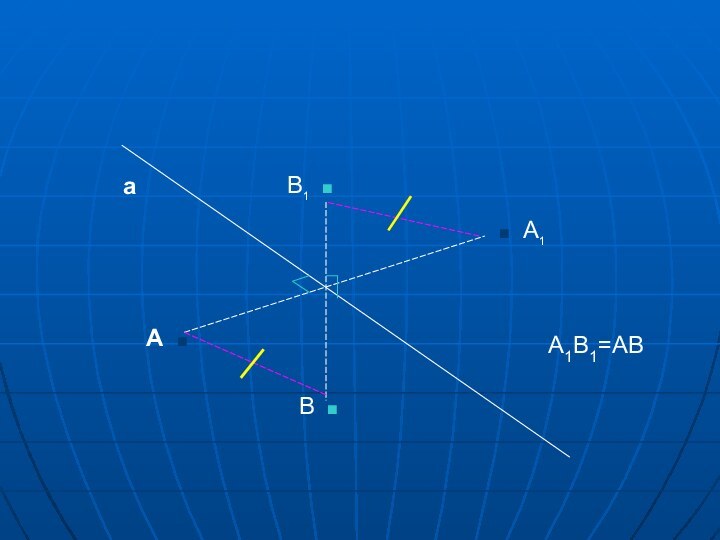
пространства на себя , при котором
любая точка М

переходит в симметричную ей точку М1
относительно оси а.

. М

а

. М1

, при котором любые две точки А и В

переходят в какие-то точки А1 и В1 так , что А1В1=АВ.
Движение пространства - это отображение пространства на себя ,сохраняющее расстояние между точками.

А(x2;y2;z2); B(x3;y3;z3)
До-ть:что осевая симметрия является движением. (AB=A1B1)

Решение:
Если М не принадлежит OZ ,то ось OZ:
1)проходит через середину отрезка ММ1.
2)перпендикулярна к нему.
Из 1усл.по формулам получаем (x+x1)/2 и (y+y1)/2 , откуда x1=-x и y1=-y.
Из усл. №2 :z1=z.
Полученные формулы равны если т-а М лежит на оси Oz.

точками получаем:

AB= (x3-x2)2+(y3-y2)2+(z3-z2)2 ,

A1B1= (-x3+x2)2 +(-y3+y2)2 +(z3-z2)2

=> AB=A1B1

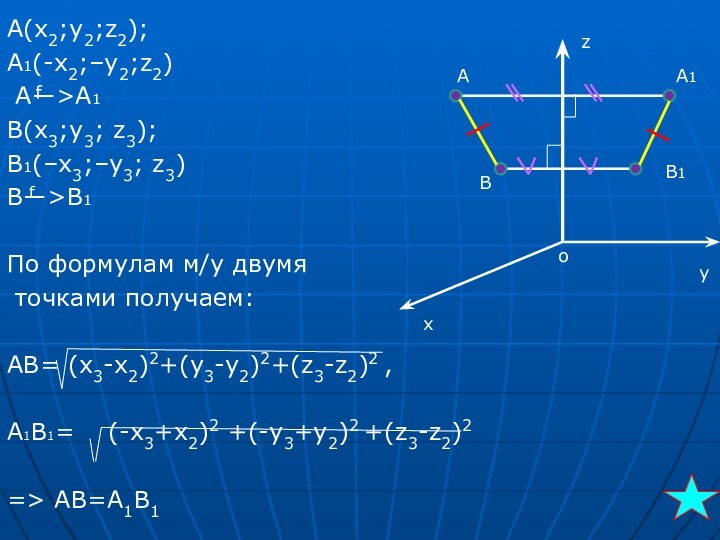
A

A1

B

B1

z

x

y

o

f

f

, В(3;-1;4) , С(1;0;-2) при: осевой симметрии относительно координатных

осей.

В1 ,С1
Решение : Выберим произвольную ось симметрии Oz.Если т-и

не лежат на оси симметрии ,то ось Oz проходит ч/з середину отрезка АА1 , ВВ1 и СС1 к ним =>
x1=-x и y1=-y и z1=z =>
А(0;-1;2), В(-3;1;4), С(-1;0;-2)
Ответ: А(0;-1;2), В(-3;1;4), С(-1;0;-2)

прямая, параллельная оси симметрии, отображается на прямую, параллелью оси

симметрии