- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Комплексные числа
Содержание
- 2. ОБЯЗАТЕЛЬНЫЙ МИНИМУМ СОДЕРЖАНИЯ ОСНОВНЫХ ОБРАЗОВАТЕЛЬНЫХ ПРОГРАММ ЧИСЛОВЫЕ
- 3. Понятие комплексного числаХ+А=В - недостаточно положительных
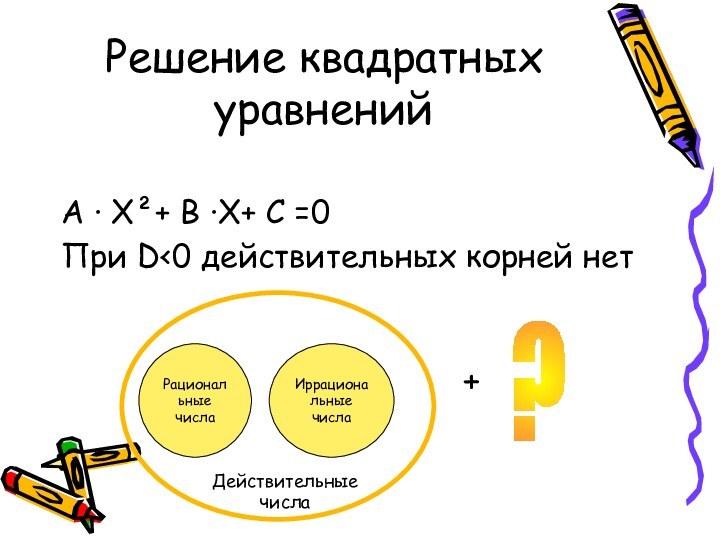
- 5. Решение квадратных уравненийА · Х²+ В ·Х+ С =0При D
- 6. Комплексные числа
- 7. Вид комплексного числаХ²=-1Х=i -корень уравненияi-
- 8. А и В – действительные числаi- некоторый
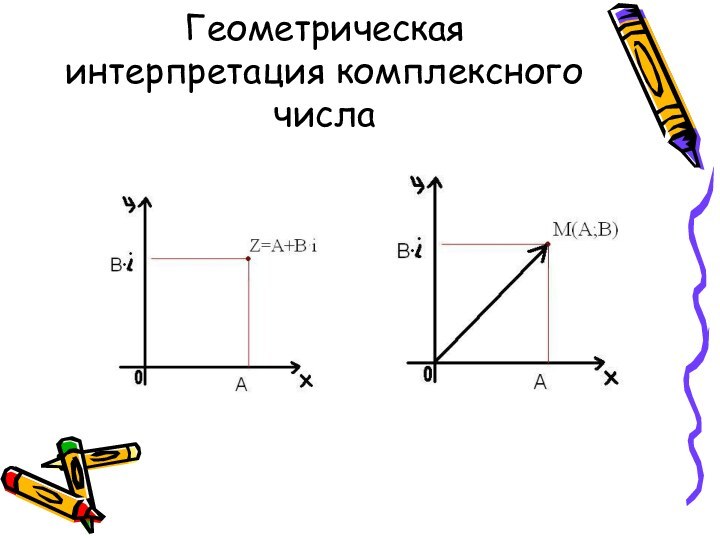
- 9. Геометрическая интерпретация комплексного числа
- 10. Модуль комплексного числаZ=А - В· iСОПРЯЖЕННОЕZ= А
- 11. Тригонометрическая форма комплексного числа Z =rφ- аргумент
- 12. Т.к Z =r =Z= А
- 13. Сложение и умножение комплексных чиселАлгебраическая формаГеометрическая формаСумма(A+iB)
- 14. Если Z 1= Z2, то получимZ²=[r (cos
- 15. Число Z называется корнем степени n
- 16. Вторая формула Муавра определяет все корни двучленного
- 17. Пример:Решить уравнение:
- 18. Свойства сложения и умноженияПереместительное свойство:Сочетательное свойство:Распределительные свойство:Z1
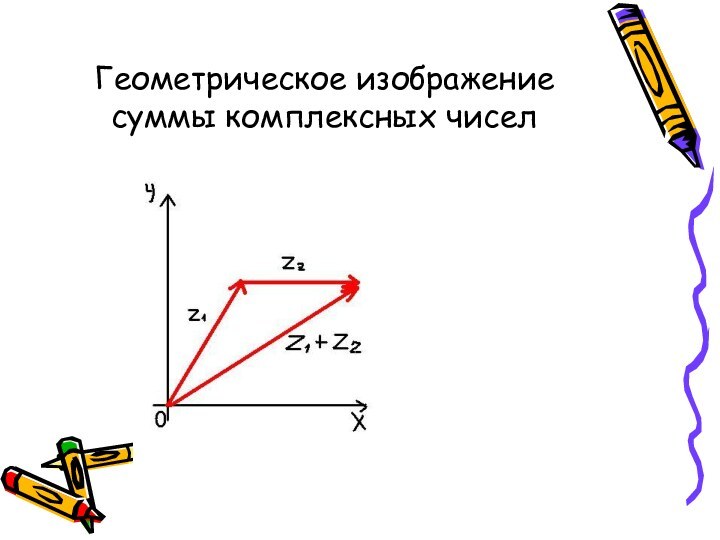
- 19. Геометрическое изображение суммы комплексных чисел
- 20. Вычитание и деление комплексных чиселZ+ Z2 =
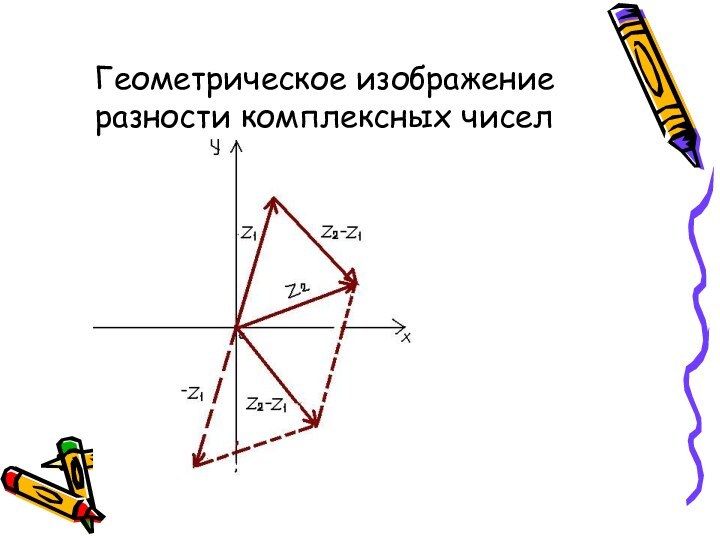
- 21. Геометрическое изображение разности комплексных чисел
- 22. Примеры:Найти разность и частное комплексных чиселРешение:
- 23. Скачать презентацию
- 24. Похожие презентации
ОБЯЗАТЕЛЬНЫЙ МИНИМУМ СОДЕРЖАНИЯ ОСНОВНЫХ ОБРАЗОВАТЕЛЬНЫХ ПРОГРАММ ЧИСЛОВЫЕ И БУКВЕННЫЕ ВЫРАЖЕНИЯ Комплексные числа. Геометрическая интерпретация комплексных чисел. Действительная и мнимая часть, модуль и аргумент комплексного числа. Алгебраическая и тригонометрическая формы записи комплексных чисел. Арифметические действия




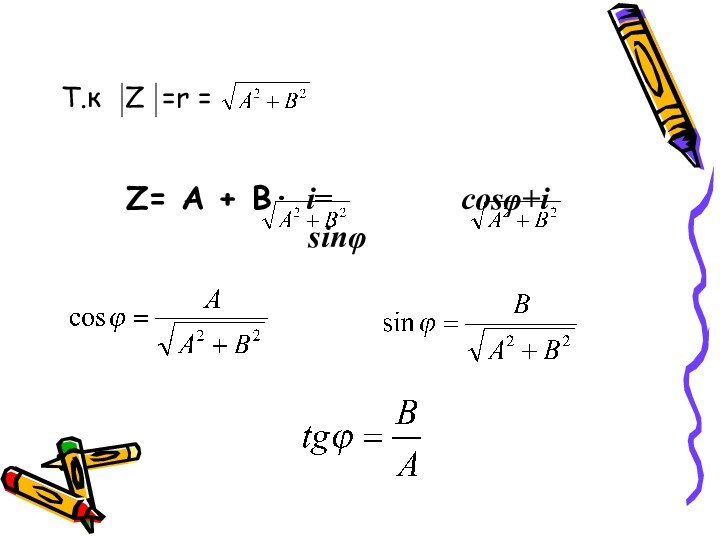

![Комплексные числа Если Z 1= Z2, то получимZ²=[r (cos φ+ i sin φ)]²=](/img/tmb/13/1283997/f3b4b6370e511a8679b3aa6f3355a946-720x.jpg)







Слайд 2
ОБЯЗАТЕЛЬНЫЙ МИНИМУМ СОДЕРЖАНИЯ
ОСНОВНЫХ ОБРАЗОВАТЕЛЬНЫХ ПРОГРАММ
ЧИСЛОВЫЕ И БУКВЕННЫЕ ВЫРАЖЕНИЯ
Слайд 3
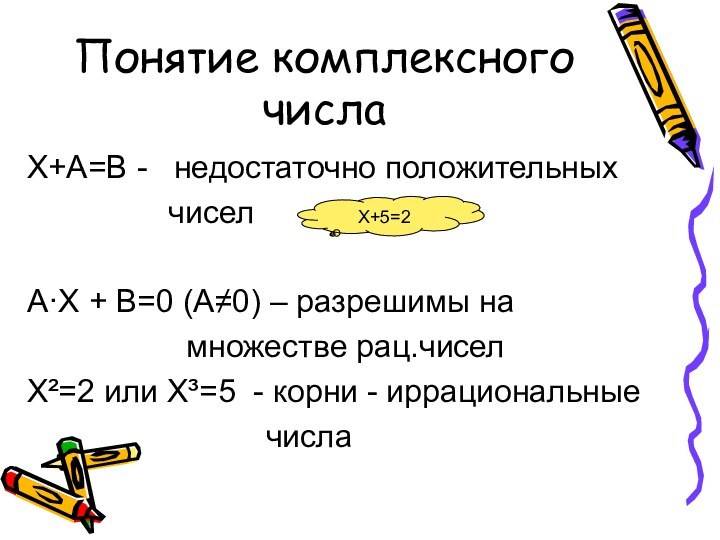
Понятие комплексного числа
Х+А=В - недостаточно положительных
чисел
А·Х +
В=0 (А≠0) – разрешимы на множестве рац.чисел
Х²=2 или Х³=5 - корни - иррациональные
числа
Х+5=2
Слайд 7
Вид комплексного числа
Х²=-1
Х=i -корень уравнения
i- комплексное
число, такое , что
i²=-1
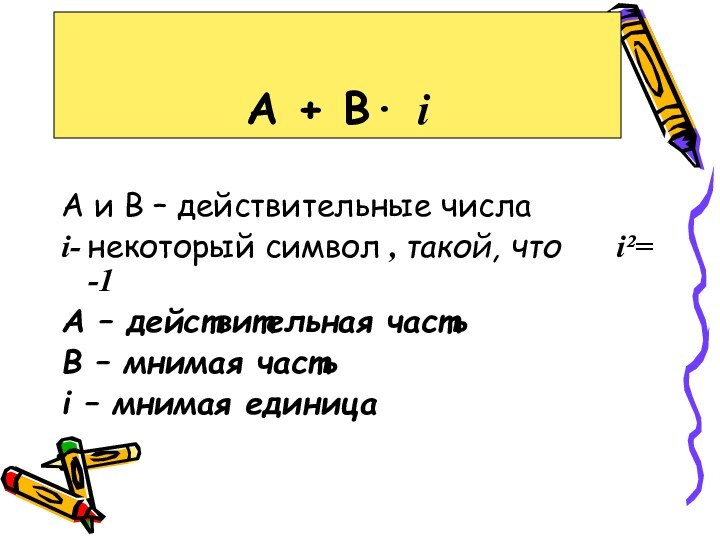
А + В· i
ЗАПИСЬ КОМПЛЕКСНОГО ЧИСЛА
В ОБЩЕМ ВИДЕ
Слайд 8
А и В – действительные числа
i- некоторый символ
, такой, что i²= -1
А – действительная часть
В
– мнимая частьi – мнимая единица
А + В· i
Слайд 10
Модуль комплексного числа
Z=А - В· i
СОПРЯЖЕННОЕ
Z= А +
В· i
(Z) = Z
Комплексно сопряженные числа.
Z = A +
B i=
Слайд 11
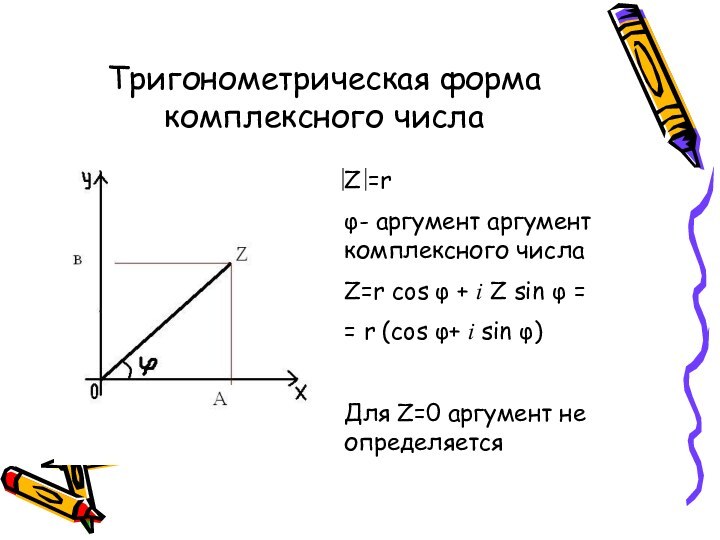
Тригонометрическая форма комплексного числа
Z =r
φ- аргумент аргумент
комплексного числа
Z=r cos φ + i Z sin φ
== r (cos φ+ i sin φ)
Для Z=0 аргумент не определяется
Слайд 13
Сложение и умножение комплексных чисел
Алгебраическая форма
Геометрическая форма
Сумма
(A+iB) +
(C+iD)=
(A+C)+(B+D)I
Произведение
Z1= r1 (cos φ1+ i sin φ1)
Z2=
r2(cos φ2+ i sin φ2)Z1 ·Z2= r1r2[cos( φ1+ φ2)+isin ( φ1+ φ2)]
Произведение
(A+iB) · (C+iD)=
(AC-BD)+(AD+BC)i
Слайд 14
Если Z 1= Z2, то получим
Z²=[r (cos φ+
i sin φ)]²=
r² (cos2 φ+ i
sin 2φ)Z³= Z²·Z=[r (cos φ+ i sin φ)]²·r (cos φ+
i sin φ)= r³ (cos3 φ+ i sin 3φ)
Формула Муавра
Для любого Z= r (cos φ+ i sin φ)≠0 и любого натурального числа n
Слайд 15
Число Z называется корнем степени n из
числа ω (обозначается ), если
(*)Из данного определения вытекает, что каждое решение уравнения
является корнем степени n из числа ω.
Z= r (cos φ+ i sin φ)
ω= ρ(cos ψ+ i sin ψ)
Вторая формула Муавра
Слайд 16 Вторая формула Муавра определяет все корни двучленного уравнения
степени n
Каждое алгебраическое уравнение степени n имеет в множестве
комплексных чисел ровно n-корней.Теорема Гаусса: каждое алгебраическое уравнение имеет в множестве комплексных чисел по крайне мере один корень
Слайд 18
Свойства сложения и умножения
Переместительное свойство:
Сочетательное свойство:
Распределительные свойство:
Z1 +
Z2 = Z1 +Z2
Z1 · Z2 = Z1 ·Z2
Z1
·(Z2 + Z3 )= Z1 · Z2+ Z1 · Z3(Z1 + Z2 )+Z3 = Z1 +(Z2+Z3)
(Z1 · Z2 ) · Z3 = Z1 ·(Z2 · Z3)
Слайд 20
Вычитание и деление комплексных чисел
Z+ Z2 = Z1
Вычитание – операция, обратная сложению:
Z+ Z2 +(- Z2 )=
Z1 +(- Z2 )Z= Z1 - Z2 –разность
Деление – операция, обратная умножению:
Z · Z2 = Z1
Разделив обе части на Z2 получим:





























