Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Математика

Содержание

МАТЕМАТИКА для специальности 070601.65 «Дизайн»Преподаватель Пивоварова Ирина Викторовна
ВГУЭСКафедра математики и моделирования МАТЕМАТИКА для специальности 070601.65 «Дизайн»Преподаватель Пивоварова Ирина Викторовна Содержание курсаВекторная алгебраПрямая на плоскостиКривые второго порядкаПолярная система координатПрямая и плоскость в пространствеПоверхности второго порядка Тема 1.Векторная алгебра Определение. Вектором называется направленный отрезок. Обозначение: (А – начало вектора, В – конец вектора). Определение. Нулевым вектором называется вектор, начало и конец которого совпадают. Обозначение: Определение. Расстояние между началом и концом вектора называется его длиной, или модулем. Обозначение: Определение. Векторы называются коллинеарными, если они расположены на одной прямой или Определение. Векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Определение. Два вектора называются равными, если они сонаправлены и имеют равные длины. Обозначение: Определение. Два вектора называются противоположными, если они противоположно направлены и имеют равные длины. Обозначение: Любой вектор в пространстве можно представить в видегде Модуль вектора вычисляется по формулеЕсли даны точки Определение. Линейными операциями называют операции сложения и вычитания векторов и умножения вектора на число. 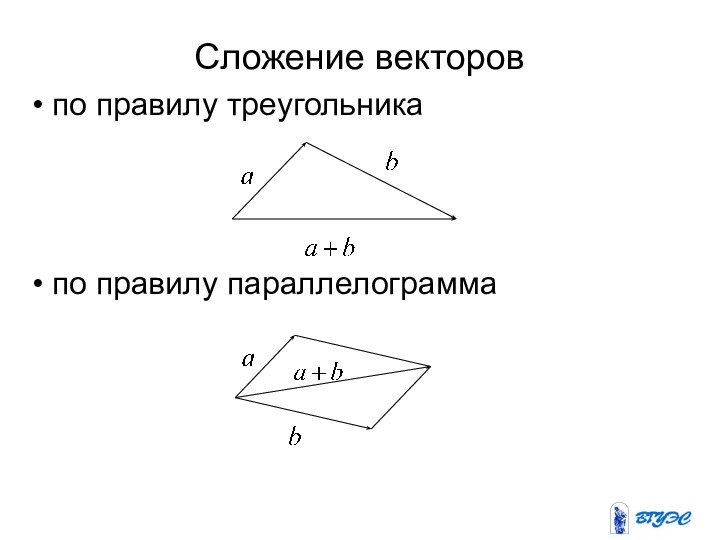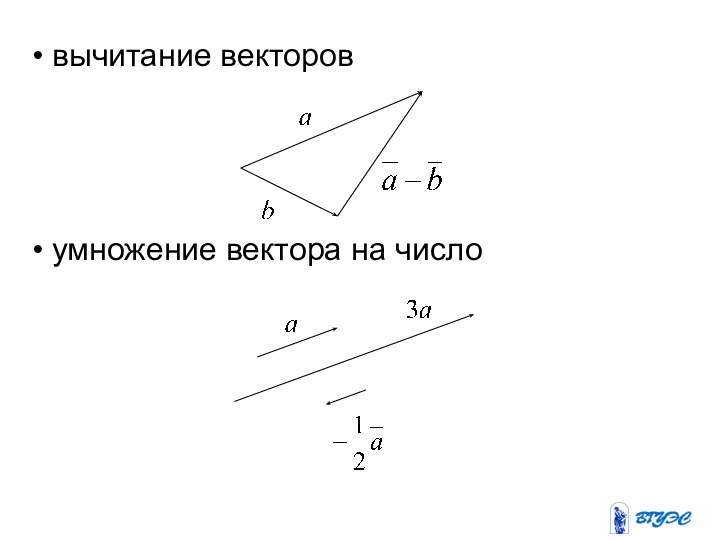Сложение векторов по правилу треугольника по правилу параллелограмма вычитание векторов умножение вектора на число Если Свойства линейных операций:1)2)3)4)5)6)7) Скалярное произведение векторов Определение. Скалярным произведением двух векторов называется число, равное произведению Выражение скалярного произведения через координаты перемножаемых векторов: Свойства скалярного произведения:1)2)3)4) Ключевые понятияВектор, модуль вектора, коллинеарные векторы, компланарные векторы, координаты вектора, скалярное произведение векторов. Вопросы для самопроверкипо теме «Векторная алгебра»Дайте определения вектора, нулевого вектора, длины вектора, Тема 2.Прямая на плоскости Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору: Общее уравнение прямой: – Уравнение прямой, проходящей через данную точку параллельно данному вектору (каноническое уравнение прямой): Уравнение прямой, проходящей через две данные точки: Уравнение прямой, проходящей через данную точку в заданном направлении: Уравнение прямой с угловым коэффициентом: – Угол между двумя прямыми: – угловые коэффициенты прямых. Условие параллельности двух прямых: Условие перпендикулярности двух прямых:где Расстояние от точки Ключевые понятияПрямая, параллельные прямые, перпендикулярные прямые, нормальный вектор прямой, направляющий вектор прямой, угловой коэффициент прямой. Вопросы для самопроверкипо теме «Прямая на плоскости»Различные виды уравнений прямой на плоскости.Какой Тема 3.Кривые второго порядка Окружность Определение. Окружностью называется множество всех точек плоскости, равноудаленных от данной точки, называемой центром. Уравнение окружности:R – радиус окружности, – центр окружности. В частности, если центр окружности находится в начале координат, то уравнение окружности:R График окружности Эллипс Определение. Эллипсом называется множество всех точек плоскости, для каждой из которых Каноническое уравнение эллипса:a , b – большая и малая полуоси эллипса,c График эллипса Гипербола Определение. Гиперболой называется множество всех точек плоскости, для каждой из которых Каноническое уравнение гиперболы:a , b – действительная и мнимая полуоси гиперболы,c График гиперболы Парабола Определение. Параболой называется множество всех точек плоскости, равноудаленных от данной точки, Каноническое уравнение параболы (соответствие вида и графика):p – параметр параболы, (p > 0). Каноническое уравнение параболы (соответствие вида и графика):p – параметр параболы, (p > 0). Ключевые понятияОкружность, эллипс, гипербола, парабола, фокусы, директриса, центр линии, вершины кривых, большая Вопросы для самопроверкипо теме «Кривые второго порядка»Определения окружности, эллипса, гиперболы, параболы.Где располагаются Тема 4.Полярная система координат O – полюс, Op – полярная ось,r – полярный радиус точки M, Координатные линии:r = const – концентрические окружности с центром в полюсе Координатные линии: – лучи, выходящие из полюса 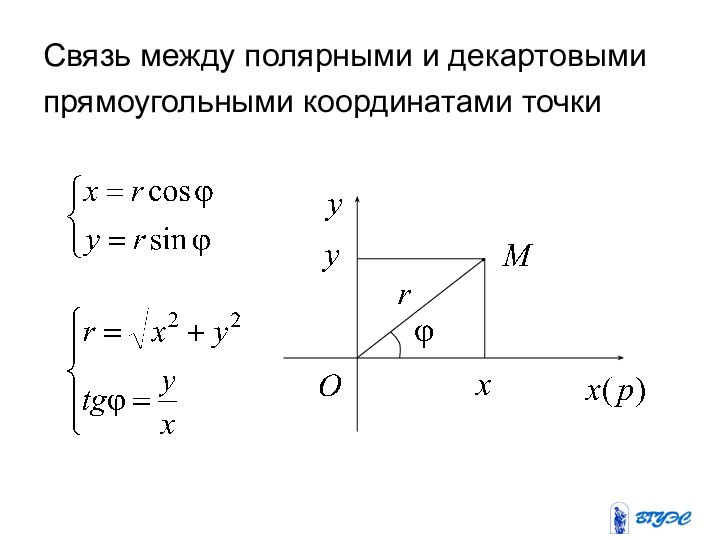Связь между полярными и декартовыми прямоугольными координатами точки Ключевые понятияПолюс, полярная ось, полярные координаты точки, полярный радиус, полярный угол, координатные линии Вопросы для самопроверкипо теме «Полярная система координат»Как определяются полярные координаты точки?Что такое Тема 5.Прямая и плоскостьв пространстве Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору: Общее уравнение плоскости: Условие параллельности двух плоскостей: Условие перпендикулярности двух плоскостей: Уравнение прямой, проходящей через данную точку параллельно данному вектору (каноническое уравнение прямой): Уравнение прямой, проходящей через две данные точки: Условие параллельности двух прямых: Условие перпендикулярности двух прямых: Условие параллельности прямой и плоскости: Условие перпендикулярности прямой и плоскости: Расстояние от точки Ключевые понятияПрямая, плоскость, параллельные прямые и плоскости, перпендикулярные прямые и плоскости, нормальный Вопросы для самопроверкипо теме «Прямая и плоскость в пространстве»Различные виды уравнений прямой Тема 6.Поверхности второго порядка Цилиндрические поверхностиОпределение. Цилиндрической поверхностью называется поверхность, составленная из всех прямых, пересекающих данную Если направляющая цилиндрической поверхности лежит в одной из координатных плоскостей, а образующие Уравнение эллиптического цилиндра:Направляющая этой поверхности – эллипс, лежащий в плоскости Оху, а Уравнение гиперболического цилиндра:Его направляющая – гипербола, лежащая в плоскости Оуz, образующие параллельны оси Ох. Уравнение параболического цилиндра:Его направляющая – парабола, лежащая в плоскости Охz, образующие параллельны оси Оу. Конические поверхностиОпределение. Конической поверхностью называется поверхность, составленная из всех прямых, пересекающих данную В частности, если направляющей конической поверхности является эллипс с полуосями a и ЭллипсоидОпределение. Эллипсоидом называется поверхность, которая в некоторой декартовой прямоугольной системе координат определяется уравнением Однополостный гиперболоидОпределение. Однополостным гиперболоидом называется поверхность, которая в некоторой декартовой прямоугольной системе координат определяется уравнением Двуполостный гиперболоидОпределение. Двуполостным гиперболоидом называется поверхность, которая в некоторой декартовой прямоугольной системе координат определяется уравнением Эллиптический параболоидОпределение. Эллиптическим параболоидом называется поверхность, которая в некоторой декартовой прямоугольной системе координат определяется уравнением Гиперболический параболоидОпределение. Гиперболическим параболоидом называется поверхность, которая в некоторой декартовой прямоугольной системе координат определяется уравнением Ключевые понятияЦилиндрическая поверхность, коническая поверхность, эллипсоид, однополостный и двуполостный гиперболоиды, эллиптический и гиперболический параболоиды. Вопросы для самопроверкипо теме «Поверхности второго порядка»Определения различных поверхностей второго порядка: цилиндрической Рекомендуемая литература1. Голодная Н.Ю., Пивоварова И.В. Аналитическая геометрия. – Владивосток: Изд-во ВГУЭС, 2008. Использование материалов презентацииИспользование данной презентации может осуществляться только при условии соблюдения требований
Слайды презентации

Слайд 2 МАТЕМАТИКА для специальности 070601.65 «Дизайн»
Преподаватель Пивоварова Ирина Викторовна

МАТЕМАТИКА для специальности 070601.65 «Дизайн»Преподаватель Пивоварова Ирина Викторовна

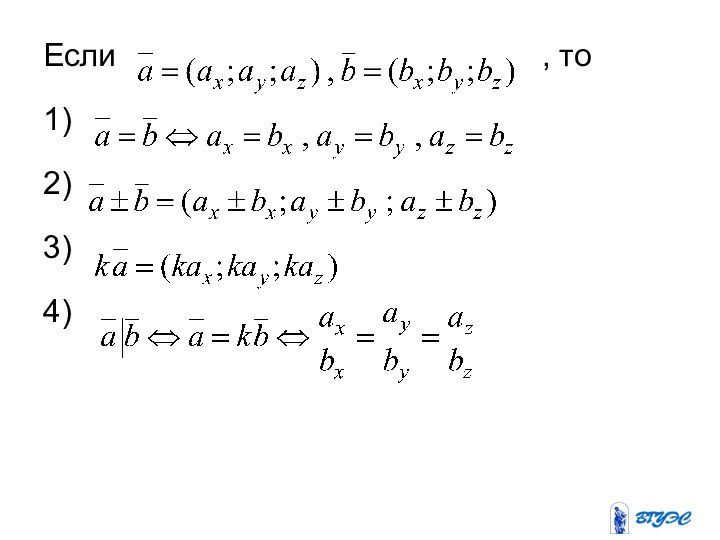
Слайд 3 Содержание курса
Векторная алгебра
Прямая на плоскости
Кривые второго порядка
Полярная система

Содержание курсаВекторная алгебраПрямая на плоскостиКривые второго порядкаПолярная система координатПрямая и плоскость в пространствеПоверхности второго порядка

координат
Прямая и плоскость в пространстве
Поверхности второго порядка

Слайд 4 Тема 1.
Векторная алгебра

Тема 1.Векторная алгебра

Слайд 5

Определение. Вектором называется направленный отрезок.

Обозначение:

Определение. Вектором называется направленный отрезок. Обозначение: (А – начало вектора, В – конец вектора).

(А – начало вектора, В – конец вектора).


Слайд 6

Определение. Нулевым вектором называется вектор, начало и

Определение. Нулевым вектором называется вектор, начало и конец которого совпадают. Обозначение:

конец которого совпадают.

Обозначение:


Слайд 7

Определение. Расстояние между началом и концом вектора

Определение. Расстояние между началом и концом вектора называется его длиной, или модулем. Обозначение:

называется его длиной, или модулем.

Обозначение:


Слайд 8 Определение. Векторы называются коллинеарными, если они расположены

Определение. Векторы называются коллинеарными, если они расположены на одной прямой

на одной прямой или на параллельных прямых.

Обозначение:

векторы сонаправлены
векторы противоположно направлены







Слайд 9


Определение. Векторы называются компланарными, если они лежат

Определение. Векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.

в одной плоскости или в параллельных плоскостях.


Слайд 10

Определение. Два вектора называются равными, если они

Определение. Два вектора называются равными, если они сонаправлены и имеют равные длины. Обозначение:

сонаправлены и имеют равные длины.

Обозначение:




Слайд 11

Определение. Два вектора называются противоположными, если они

Определение. Два вектора называются противоположными, если они противоположно направлены и имеют равные длины. Обозначение:

противоположно направлены и имеют равные длины.

Обозначение:


Слайд 12 Любой вектор в пространстве можно представить в виде

где

Любой вектор в пространстве можно представить в видегде

– единичные

векторы, направленные соответственно вдоль осей Ox, Oy, Oz (орты осей);
– координаты вектора:
или




Слайд 13 Модуль вектора вычисляется по формуле


Если даны точки

Модуль вектора вычисляется по формулеЕсли даны точки

и , то



Слайд 14

Определение. Линейными операциями называют операции сложения и

Определение. Линейными операциями называют операции сложения и вычитания векторов и умножения вектора на число.

вычитания векторов и умножения вектора на число.


Слайд 15 Сложение векторов
по правилу треугольника



по правилу

Сложение векторов по правилу треугольника по правилу параллелограмма

параллелограмма



Слайд 16 вычитание векторов



умножение вектора на число



вычитание векторов умножение вектора на число

Слайд 17 Если

Если , то 1)2)3)4)

, то
1)
2)
3)
4)




Слайд 18 Свойства линейных операций:
1)
2)
3)
4)
5)
6)
7)










Свойства линейных операций:1)2)3)4)5)6)7)

Слайд 19 Скалярное произведение векторов

Определение. Скалярным произведением двух векторов

Скалярное произведение векторов Определение. Скалярным произведением двух векторов называется число, равное

называется число, равное произведению длин этих векторов на косинус

угла между ними:





Слайд 20
Выражение скалярного произведения через координаты перемножаемых векторов:


Выражение скалярного произведения через координаты перемножаемых векторов:

Слайд 21 Свойства скалярного произведения:
1)
2)
3)
4)

Свойства скалярного произведения:1)2)3)4) , или , или5)

,

или , или
5)


















Слайд 22 Ключевые понятия

Вектор, модуль вектора, коллинеарные векторы, компланарные векторы,

Ключевые понятияВектор, модуль вектора, коллинеарные векторы, компланарные векторы, координаты вектора, скалярное произведение векторов.

координаты вектора, скалярное произведение векторов.

Слайд 23 Вопросы для самопроверки
по теме «Векторная алгебра»
Дайте определения вектора,

Вопросы для самопроверкипо теме «Векторная алгебра»Дайте определения вектора, нулевого вектора, длины

нулевого вектора, длины вектора, коллинеарных векторов, компланарных векторов, равных

векторов, противоположных векторов, скалярного произведения векторов.
Как определяются сумма векторов, разность векторов, произведение вектора на число?
Как выражается скалярное произведение через координаты перемножаемых векторов?
Сформулируйте условия коллинеарности и перпендикулярности векторов.

Слайд 24 Тема 2.
Прямая на плоскости

Тема 2.Прямая на плоскости

Слайд 25
Уравнение прямой, проходящей через данную точку перпендикулярно данному

Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору:

вектору:


– вектор, перпендикулярный прямой (нормальный вектор прямой),
– заданная точка на прямой.



Слайд 26
Общее уравнение прямой:


Общее уравнение прямой: – вектор, перпендикулярный прямой (нормальный вектор прямой).

– вектор, перпендикулярный прямой (нормальный вектор

прямой).



Слайд 27 Уравнение прямой, проходящей через данную точку параллельно данному

Уравнение прямой, проходящей через данную точку параллельно данному вектору (каноническое уравнение

вектору (каноническое уравнение прямой):


– вектор, параллельный прямой (направляющий вектор прямой),
– заданная точка на прямой.



Слайд 28
Уравнение прямой, проходящей через две данные точки:



Уравнение прямой, проходящей через две данные точки:

– заданные точки на прямой.








Слайд 29
Уравнение прямой, проходящей через данную точку в заданном

Уравнение прямой, проходящей через данную точку в заданном направлении:

направлении:


– угловой коэффициент прямой
( – угол между прямой и осью Ox),
– заданная точка на прямой.



Слайд 30
Уравнение прямой с угловым коэффициентом:


Уравнение прямой с угловым коэффициентом: – угловой коэффициент

– угловой коэффициент прямой
(

– угол между прямой и осью Ox),
b – отрезок, отсекаемый прямой на оси Oy.



Слайд 31
Угол между двумя прямыми:



Угол между двумя прямыми: – угловые коэффициенты прямых.

– угловые коэффициенты прямых.











Слайд 32 Условие параллельности двух прямых:


Условие перпендикулярности двух

Условие параллельности двух прямых: Условие перпендикулярности двух прямых:где – угловые коэффициенты прямых.

прямых:


где – угловые

коэффициенты прямых.












Слайд 33
Расстояние от точки

Расстояние от точки до прямой :

до прямой

:












Слайд 34 Ключевые понятия

Прямая, параллельные прямые, перпендикулярные прямые, нормальный вектор

Ключевые понятияПрямая, параллельные прямые, перпендикулярные прямые, нормальный вектор прямой, направляющий вектор прямой, угловой коэффициент прямой.

прямой, направляющий вектор прямой, угловой коэффициент прямой.

Слайд 35 Вопросы для самопроверки
по теме «Прямая на плоскости»
Различные виды

Вопросы для самопроверкипо теме «Прямая на плоскости»Различные виды уравнений прямой на

уравнений прямой на плоскости.
Какой вектор называется нормальным, направляющим вектором

прямой?
Как определяется угловой коэффициент прямой?
В каком случае k = 0? k не существует?
Условия параллельности и перпендикулярности прямых.

Слайд 36 Тема 3.
Кривые второго порядка

Тема 3.Кривые второго порядка

Слайд 37 Окружность

Определение. Окружностью называется множество всех точек плоскости,

Окружность Определение. Окружностью называется множество всех точек плоскости, равноудаленных от данной точки, называемой центром.

равноудаленных от данной точки, называемой центром.




Слайд 38
Уравнение окружности:


R – радиус окружности,

Уравнение окружности:R – радиус окружности, – центр окружности.

– центр окружности.



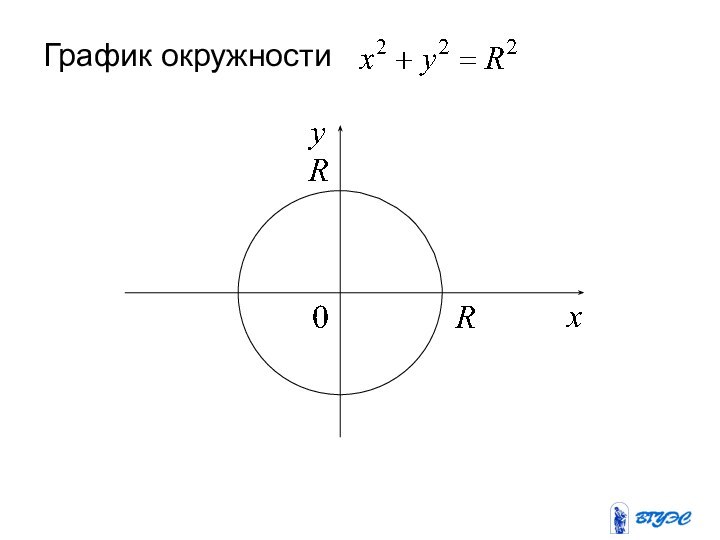
Слайд 39
В частности, если центр окружности находится в начале

В частности, если центр окружности находится в начале координат, то уравнение

координат, то уравнение окружности:


R – радиус окружности,

– центр окружности.




Слайд 40 График окружности


График окружности

Слайд 41 Эллипс

Определение. Эллипсом называется множество всех точек плоскости,

Эллипс Определение. Эллипсом называется множество всех точек плоскости, для каждой из

для каждой из которых сумма расстояний до двух данных

точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.





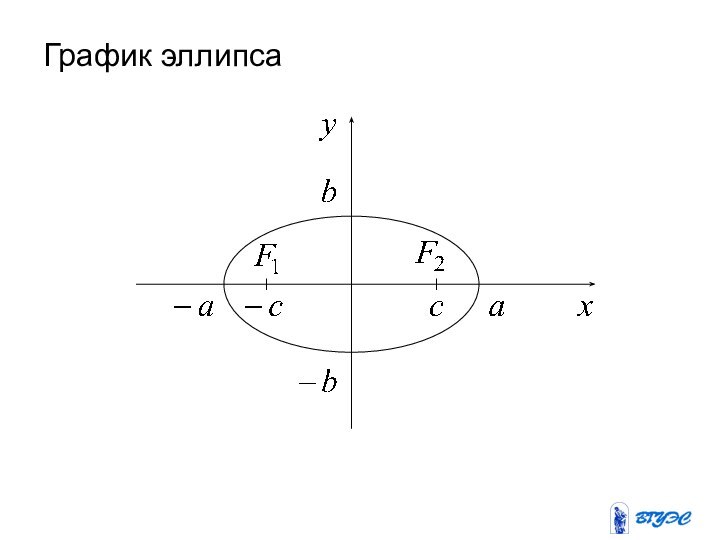
Слайд 42
Каноническое уравнение эллипса:


a , b – большая и

Каноническое уравнение эллипса:a , b – большая и малая полуоси эллипса,c – половина расстояния между фокусами,

малая полуоси эллипса,
c – половина расстояния между фокусами,



Слайд 43 График эллипса


График эллипса

Слайд 44 Гипербола

Определение. Гиперболой называется множество всех точек плоскости,

Гипербола Определение. Гиперболой называется множество всех точек плоскости, для каждой из

для каждой из которых модуль разности расстояний до двух

данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.





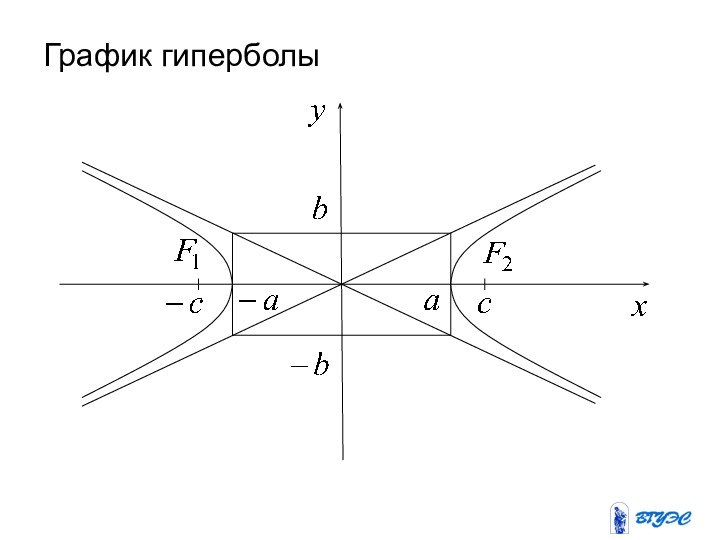
Слайд 45 Каноническое уравнение гиперболы:


a , b – действительная и

Каноническое уравнение гиперболы:a , b – действительная и мнимая полуоси гиперболы,c

мнимая полуоси гиперболы,
c – половина расстояния между фокусами,

– асимптоты гиперболы.




Слайд 46 График гиперболы


График гиперболы

Слайд 47 Парабола

Определение. Параболой называется множество всех точек плоскости,

Парабола Определение. Параболой называется множество всех точек плоскости, равноудаленных от данной

равноудаленных от данной точки, называемой фокусом, и данной прямой,

называемой директрисой.





Слайд 48 Каноническое уравнение параболы (соответствие вида и графика):
p –

Каноническое уравнение параболы (соответствие вида и графика):p – параметр параболы, (p > 0).

параметр параболы, (p > 0).



Слайд 49 Каноническое уравнение параболы (соответствие вида и графика):
p –

Каноническое уравнение параболы (соответствие вида и графика):p – параметр параболы, (p > 0).

параметр параболы, (p > 0).



Слайд 50 Ключевые понятия

Окружность, эллипс, гипербола, парабола, фокусы, директриса, центр

Ключевые понятияОкружность, эллипс, гипербола, парабола, фокусы, директриса, центр линии, вершины кривых,

линии, вершины кривых, большая и малая полуоси, действительная и

мнимая полуоси.

Слайд 51 Вопросы для самопроверки
по теме «Кривые второго порядка»
Определения окружности,

Вопросы для самопроверкипо теме «Кривые второго порядка»Определения окружности, эллипса, гиперболы, параболы.Где

эллипса, гиперболы, параболы.
Где располагаются фокусы эллипса, гиперболы, параболы?
Канонические уравнения

окружности, эллипса, гиперболы, параболы.
Графики окружности, эллипса, гиперболы, параболы.
Асимптоты гиперболы.

Слайд 52 Тема 4.
Полярная система координат

Тема 4.Полярная система координат

Слайд 53 O – полюс, Op – полярная ось,
r –

O – полюс, Op – полярная ось,r – полярный радиус точки

полярный радиус точки M,
– полярный угол

точки M,
r , – полярные координаты точки M.





Слайд 54 Координатные линии:

r = const – концентрические окружности с

Координатные линии:r = const – концентрические окружности с центром в полюсе

центром в полюсе




Слайд 55 Координатные линии:

Координатные линии: – лучи, выходящие из полюса

– лучи, выходящие из полюса




Слайд 56 Связь между полярными и декартовыми прямоугольными координатами точки




Связь между полярными и декартовыми прямоугольными координатами точки

Слайд 57 Ключевые понятия

Полюс, полярная ось, полярные координаты точки, полярный

Ключевые понятияПолюс, полярная ось, полярные координаты точки, полярный радиус, полярный угол, координатные линии

радиус, полярный угол, координатные линии

Слайд 58 Вопросы для самопроверки
по теме «Полярная система координат»
Как определяются

Вопросы для самопроверкипо теме «Полярная система координат»Как определяются полярные координаты точки?Что

полярные координаты точки?
Что такое полярный радиус, полярный угол точки?
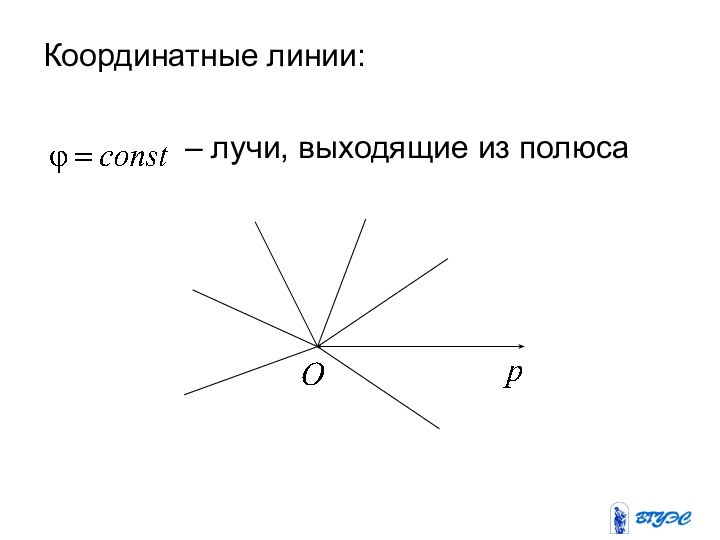
Какие

линии определяют уравнения r = const ,
ϕ = const ?
Какие координаты имеет полюс?
Как связаны декартовы прямоугольные и полярные координаты точки?

Слайд 59 Тема 5.
Прямая и плоскость
в пространстве

Тема 5.Прямая и плоскостьв пространстве

Слайд 60 Уравнение плоскости, проходящей через данную точку перпендикулярно данному

Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору:

вектору:


– вектор, перпендикулярный плоскости (нормальный вектор плоскости),
– заданная точка на плоскости.



Слайд 61
Общее уравнение плоскости:


Общее уравнение плоскости: – вектор, перпендикулярный плоскости (нормальный вектор плоскости).

– вектор, перпендикулярный плоскости (нормальный

вектор плоскости).



Слайд 62 Условие параллельности двух плоскостей:


Условие перпендикулярности двух

Условие параллельности двух плоскостей: Условие перпендикулярности двух плоскостей:

плоскостей:











Слайд 63 Уравнение прямой, проходящей через данную точку параллельно данному

Уравнение прямой, проходящей через данную точку параллельно данному вектору (каноническое уравнение

вектору (каноническое уравнение прямой):


– вектор, параллельный прямой (направляющий вектор прямой),
– заданная точка на прямой.



Слайд 64
Уравнение прямой, проходящей через две данные точки:



Уравнение прямой, проходящей через две данные точки:

– заданные точки на прямой.








Слайд 65 Условие параллельности двух прямых:



Условие перпендикулярности двух

Условие параллельности двух прямых: Условие перпендикулярности двух прямых:

прямых:











Слайд 66 Условие параллельности прямой и плоскости:



Условие перпендикулярности

Условие параллельности прямой и плоскости: Условие перпендикулярности прямой и плоскости:

прямой и плоскости:











Слайд 67
Расстояние от точки

Расстояние от точки до плоскости

до плоскости

:












Слайд 68 Ключевые понятия

Прямая, плоскость, параллельные прямые и плоскости, перпендикулярные

Ключевые понятияПрямая, плоскость, параллельные прямые и плоскости, перпендикулярные прямые и плоскости,

прямые и плоскости, нормальный вектор плоскости, направляющий вектор прямой.

Слайд 69 Вопросы для самопроверки
по теме «Прямая и плоскость в

Вопросы для самопроверкипо теме «Прямая и плоскость в пространстве»Различные виды уравнений

пространстве»
Различные виды уравнений прямой и плоскости в пространстве.
Какой вектор

называется нормальным вектором плоскости, направляющим вектором прямой?
Как определяется расстояние от точки до плоскости?
Условия параллельности и перпендикулярности двух прямых, двух плоскостей, прямой и плоскости.

Слайд 70 Тема 6.
Поверхности второго порядка

Тема 6.Поверхности второго порядка

Слайд 71 Цилиндрические поверхности
Определение. Цилиндрической поверхностью называется поверхность, составленная из

Цилиндрические поверхностиОпределение. Цилиндрической поверхностью называется поверхность, составленная из всех прямых, пересекающих

всех прямых, пересекающих данную линию L и параллельных данной

прямой. Линия L при этом называется направляющей цилиндрической поверхности, а каждая из прямых, составляющих поверхность и параллельных прямой, - ее образующей.



Слайд 72 Если направляющая цилиндрической поверхности лежит в одной из

Если направляющая цилиндрической поверхности лежит в одной из координатных плоскостей, а

координатных плоскостей, а образующие параллельны координатной оси, перпендикулярной этой

плоскости, то уравнение такой поверхности совпадает с уравнением направляющей L, то есть содержит только две переменных.



Слайд 73
Уравнение эллиптического цилиндра:



Направляющая этой поверхности – эллипс, лежащий

Уравнение эллиптического цилиндра:Направляющая этой поверхности – эллипс, лежащий в плоскости Оху,

в плоскости Оху, а образующие параллельны оси Оz .


Слайд 74
Уравнение гиперболического цилиндра:



Его направляющая – гипербола, лежащая в

Уравнение гиперболического цилиндра:Его направляющая – гипербола, лежащая в плоскости Оуz, образующие параллельны оси Ох.

плоскости Оуz, образующие параллельны оси Ох.


Слайд 75
Уравнение параболического цилиндра:


Его направляющая – парабола, лежащая в

Уравнение параболического цилиндра:Его направляющая – парабола, лежащая в плоскости Охz, образующие параллельны оси Оу.

плоскости Охz, образующие параллельны оси Оу.


Слайд 76 Конические поверхности
Определение. Конической поверхностью называется поверхность, составленная из

Конические поверхностиОпределение. Конической поверхностью называется поверхность, составленная из всех прямых, пересекающих

всех прямых, пересекающих данную линию L и проходящих через

данную точку Р. Линия L при этом называется направляющей конической поверхности, точка Р – ее вершиной, а каждая из прямых, составляющих коническую поверхность, - ее образующей.



Слайд 77 В частности, если направляющей конической поверхности является эллипс

В частности, если направляющей конической поверхности является эллипс с полуосями a

с полуосями a и b, лежащий в плоскости
z =

c, а вершина находится в начале координат, то уравнение такой поверхности имеет вид:



Слайд 78 Эллипсоид
Определение. Эллипсоидом называется поверхность, которая в некоторой декартовой

ЭллипсоидОпределение. Эллипсоидом называется поверхность, которая в некоторой декартовой прямоугольной системе координат определяется уравнением

прямоугольной системе координат определяется уравнением


Слайд 79 Однополостный гиперболоид
Определение. Однополостным гиперболоидом называется поверхность, которая в

Однополостный гиперболоидОпределение. Однополостным гиперболоидом называется поверхность, которая в некоторой декартовой прямоугольной системе координат определяется уравнением

некоторой декартовой прямоугольной системе координат определяется уравнением


Слайд 80 Двуполостный гиперболоид
Определение. Двуполостным гиперболоидом называется поверхность, которая в

Двуполостный гиперболоидОпределение. Двуполостным гиперболоидом называется поверхность, которая в некоторой декартовой прямоугольной системе координат определяется уравнением

некоторой декартовой прямоугольной системе координат определяется уравнением


Слайд 81 Эллиптический параболоид
Определение. Эллиптическим параболоидом называется поверхность, которая в

Эллиптический параболоидОпределение. Эллиптическим параболоидом называется поверхность, которая в некоторой декартовой прямоугольной системе координат определяется уравнением

некоторой декартовой прямоугольной системе координат определяется уравнением


Слайд 82 Гиперболический параболоид
Определение. Гиперболическим параболоидом называется поверхность, которая в

Гиперболический параболоидОпределение. Гиперболическим параболоидом называется поверхность, которая в некоторой декартовой прямоугольной системе координат определяется уравнением

некоторой декартовой прямоугольной системе координат определяется уравнением


Слайд 83 Ключевые понятия

Цилиндрическая поверхность, коническая поверхность, эллипсоид, однополостный и

Ключевые понятияЦилиндрическая поверхность, коническая поверхность, эллипсоид, однополостный и двуполостный гиперболоиды, эллиптический и гиперболический параболоиды.

двуполостный гиперболоиды, эллиптический и гиперболический параболоиды.

Слайд 84 Вопросы для самопроверки
по теме «Поверхности второго порядка»
Определения различных

Вопросы для самопроверкипо теме «Поверхности второго порядка»Определения различных поверхностей второго порядка:

поверхностей второго порядка: цилиндрической поверхности, конической поверхности, эллипсоида, однополостного

и двуполостного гиперболоидов, эллиптического и гиперболического параболоидов.
Различные виды уравнений поверхностей второго порядка.
Исследование формы поверхностей по их уравнениям.

Слайд 85 Рекомендуемая литература
1. Голодная Н.Ю., Пивоварова И.В. Аналитическая геометрия. –

Рекомендуемая литература1. Голодная Н.Ю., Пивоварова И.В. Аналитическая геометрия. – Владивосток: Изд-во ВГУЭС,

Владивосток: Изд-во ВГУЭС, 2008. – 36 с.
2. Дубинина Л.Я., Никулина

Л.С., Пивоварова И.В. Курс лекций по высшей математике. Часть 1. – Владивосток: Изд-во ВГУЭС, 2008. – 132 с.
  • Имя файла: matematika.pptx
  • Количество просмотров: 159
  • Количество скачиваний: 0
- Предыдущая Виды спорта
Следующая - Мир Гарри Поттера

Похожие презентации

ЕГЭ Алгебра и химия ЕГЭ Алгебра и химия 97
Математический КВН для 4 класса в виде игры Своя игра. план-конспект занятия по математике (4 класс) по теме Математический КВН для 4 класса в виде игры Своя игра. план-конспект занятия по математике (4 класс) по теме 231
Презентация по математике на тему Умножение трёхзначного числа на однозначное. презентация к уроку по математике (4 класс) Презентация по математике на тему Умножение трёхзначного числа на однозначное. презентация к уроку по математике (4 класс) 132
Проценты 5 класс Проценты 5 класс 126
Знакомство с геометрической фигурой-овал презентация к уроку по математике (средняя группа) Знакомство с геометрической фигурой-овал презентация к уроку по математике (средняя группа) 149
Презентация к уроку математики презентация урока для интерактивной доски по математике (3 класс) Презентация к уроку математики презентация урока для интерактивной доски по математике (3 класс) 106
Решение уравнений Решение уравнений 165
высота т,тембр и громкость звука высота т,тембр и громкость звука 116
Часы Часы 120
Презентация к уроку математики, посвященного юбилею школы. 2 класс Презентация к уроку математики, посвященного юбилею школы. 2 класс 114
Сумма углов треугольника Сумма углов треугольника 95
Игровые задания на решение задач в одно действие. Сложение методическая разработка по математике (подготовительная группа) по теме Игровые задания на решение задач в одно действие. Сложение методическая разработка по математике (подготовительная группа) по теме 113
Утворення і запис трицифрових чисел Утворення і запис трицифрових чисел 126
Сложение и вычитание чисел в пределах 10 презентация к уроку по математике (1 класс) по теме Сложение и вычитание чисел в пределах 10 презентация к уроку по математике (1 класс) по теме 124
Презентация внеклассного мероприятия для учащихся 6-х классов. Игра по математике Счастливый случай Презентация внеклассного мероприятия для учащихся 6-х классов. Игра по математике Счастливый случай 181
Сокращение дробей Сокращение дробей 106
Презентация задач на сложные банковские проценты с пополнением вклада Презентация задач на сложные банковские проценты с пополнением вклада 124
Музей математики Музей математики 121
Конспект НОД по математике для детей старшей группы Путешествие в Город Геометрических фигур материал по математике (старшая группа) Конспект НОД по математике для детей старшей группы Путешествие в Город Геометрических фигур материал по математике (старшая группа) 112
Смежные и вертикальные углы Смежные и вертикальные углы 183
Применение распределительного свойства умножения Применение распределительного свойства умножения 122
Конспект занятия Звездочёты. план-конспект занятия по математике (средняя группа) по теме Конспект занятия Звездочёты. план-конспект занятия по математике (средняя группа) по теме 132
Извлечение квадратного корня без калькулятора Извлечение квадратного корня без калькулятора 129
Презентация по математике на тему Великая Отечественная Война в задачах Презентация по математике на тему Великая Отечественная Война в задачах 144
Алгебра функций Алгебра функций 114
Параллелограмм Параллелограмм 107
zadachi na sravnenie urok 30 zadachi na sravnenie urok 30 153
Жазбаша көбейту және бөлу.Пысықтау сабақ план-конспект урока по математике (4 класс) Жазбаша көбейту және бөлу.Пысықтау сабақ план-конспект урока по математике (4 класс) 72
Интерактивный тренажёр Раскраска .Математика (3 класс) Интерактивный тренажёр Раскраска .Математика (3 класс) 137
Клуб веселых математиков. классный час по математике (4 класс) по теме Клуб веселых математиков. классный час по математике (4 класс) по теме 127