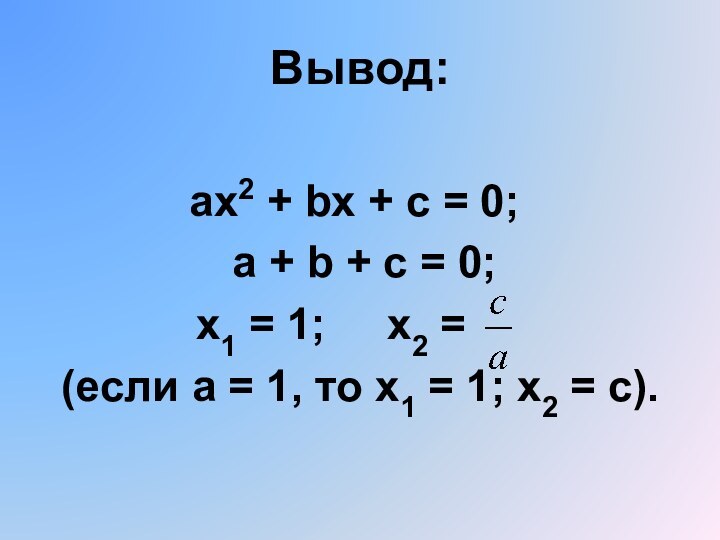Презентация на тему Квадратные уравнения

учащихся на решение квадратных уравнений, в которых а +b

+ с = 0;
Привить навыки устного решения таких уравнений.
Воспитательные цели урока
- способствовать выработке у школьников желания и потребности обобщения изучаемых фактов: развивать самостоятельность и творчество.

задач с использованием теоремы Виета.
IV Изучение нового свойства квадратных

уравнений.
V Решение задач на закрепление свойства.
VI Самостоятельная работа.
VII Задание на дом.
VIII Итог урока.

помощью тестирования.
2. Решение задач на применение прямой и

обратной теорем Виета.
3. Изучение нового свойства квадратных уравнений.

7 х2 – 9х +

2 = 0.
Решение:
D =(-9)2 – 4 * 7 * 2 = 25; D > 0.

х1 = х2 =


Ответ: 1;

с = 0-квадратное уравнение, то а называют … коэффи-
циентом,

с- … членом.
2. Уравнение х2 = а, где а < о, не имеет … .
3. Уравнение вида ах2 + с = 0, где а 0, с 0, называют … квадратным
уравнением.
4. Корни квадратного уравнения ах2 + bх + с = 0 вычисляют по
формулам

х1= х2=

5. Квадратное уравнение ах2 + bх + с = 0 имеет два различных действи-
тельных корня, если b2 – 4ас … 0.
6. Квадратное уравнение вида х2 + px + g = 0 называют … .
7. Сумма корней приведенного квадратного уравнения равна …
коэффициенту, взятому с … знаком, а произведение корней равно …
члену.
8. Если числа p, g, х1, х2 таковы, что х1 +х2 = - p, х1 * х2 = …,то х1 и х2-корни
уравнения … .

; b

.
Больше.
Приведенным.
Второму, свободному.
g, приведенного

Здесь вы видите уравнения, определенные по какому-то признаку. Как

вы думаете, какое из уравнений этой группы является лишним?

а)1. 2х2 – х = 0; б)1. х2 – 5х + 1 = 0;
2. х2 – 16 = 0; 2. х2 + 2х – 2 = 0;
3. 4х2 + х-3 = 0; 3. 9х2 – 6х + 10 = 0;
4. 2х2 = 0. 4. х2 - 3х -1 = 0.

х2 + px + g = 0

x1 + x2 = -p
x1 * x2 = g

корней теорема Виета.
Что лучше, скажи постоянства такого:
Умножишь ты корни-

и дробь уж готова?
В числителе c, в знаменателе a,
А сумма корней тоже дроби равна.
Хоть с минусом дробь, что за беда!
В числителе b, в знаменателе a.

Найти сумму и произведение корней следующих уравнений:

х1 + х2 х1 * х2
х2 – 3х – 4 = 0; ? ?
Х2 – 9х + 14 = 0; ? ?
2х2 – 5х + 18 = 0; ? ?
3х2 + 15х + 1 = 0. ? ?
Для уравнений 1), 2) найти подбором корни.

если известны его корни.

х1 =

-3 х2 + px + g = 0;
х2 = 1. х2 + 2х + (-3) = 0;
х1 + х2 = -3 + 1 = -2 p=2; g = -3;
-p = -2; p = 2 x2 + 2x – 3 = 0
х1 * х2 = g
х1 * х2 = -3; g =-3.

1. х1 = 5, 2. х1 = -5, 3. х1 = 5, 4. х1 = -5,
х2 = -6 х2 = 6 х2 = -6 х2 = -6

– 11х + 30 = 0.
2)

х2 – х – 30 = 0.
3) х2 + х – 30 = 0.
4) х2 + 11х + 30 = 0.

коэффициенты а каждом уравнении и найдите сумму коэффициентов.

сумма
коэффициентов

х2 – 5х + 1 = 0; 1 – 5 + 1 = -3.
9х2 – 6х + 10 = 0; 9 – 6 + 10 = 13.
Х2 + 2х -2 = 0; 1 + 2 – 2 = 1.
Х2 -3х – 1 = 0; 1 – 3 – 1 = -3.

изучению нового свойства.

сумма
коэффициентов
х2 + 2х – 3 = 0; х1 = 1; х2 = -3 0
х2 + х – 2 = 0; х1 = 1; х2 = -2 0
х2 – 3х + 2 = 0; х1 = 1; х2 = 2 0

5х2 -8х + 3 = 0; х1 = 1; х2 = 0

ах2 + bx + c = 0;

a + b + c = 0;
x1 = 1; x2 =
(если а = 1, то х1 = 1; х2 = с).

(а,б,д)

2. Обратить внимание на уравнение, которое было решено в

начале урока.
7х2 – 9х + 2 = 0;
7 – 9 + 2 = 0;

х1 = 1; х2 =

3. Сделать вывод о значимости данного свойства.

Вариант 2.
1) х2 + 23 – 24 = 0; 1) х2 + 15х -16 = 0;
2) 2х2 + х – 3 = 0; 2) 5х2 + х -6 = 0;
3) -5х2 + 4,4х + 0,6 = 0; 3) -2х2 + 1,7х + 0,3 = 0;

4) х2 + х – 3 = 0. 4) х2 + х – 4 = 0.