Презентация на тему Мастер -класс Использование презентаций Power Point на урока математики при построении графиков функции

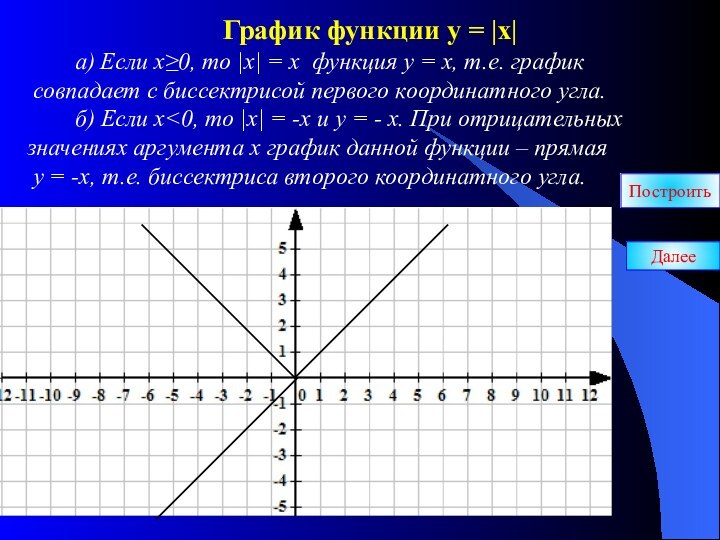
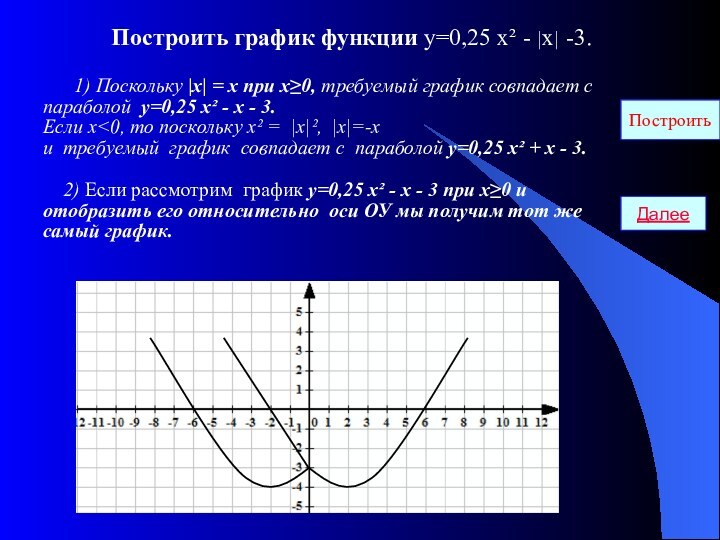
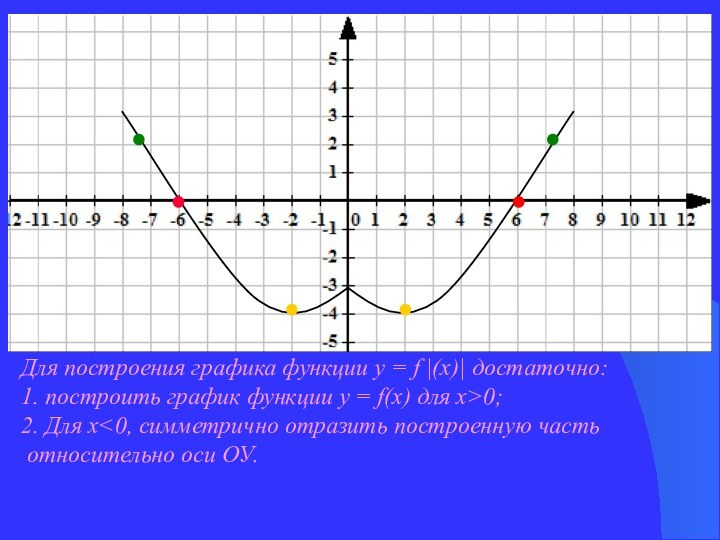
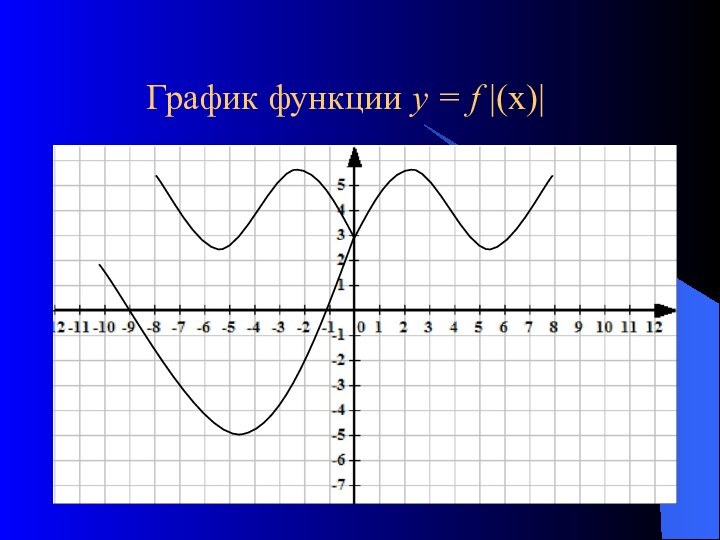
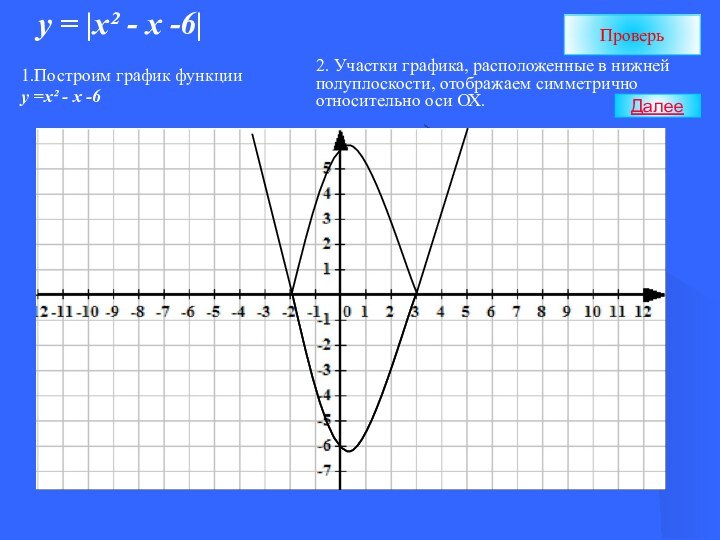
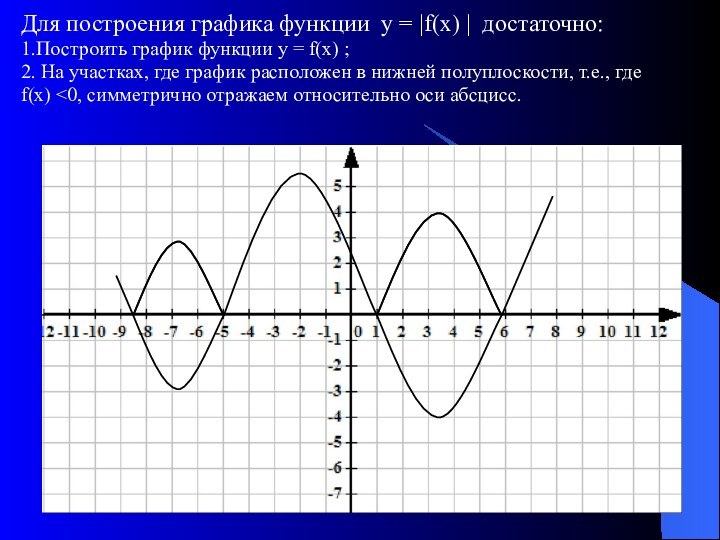
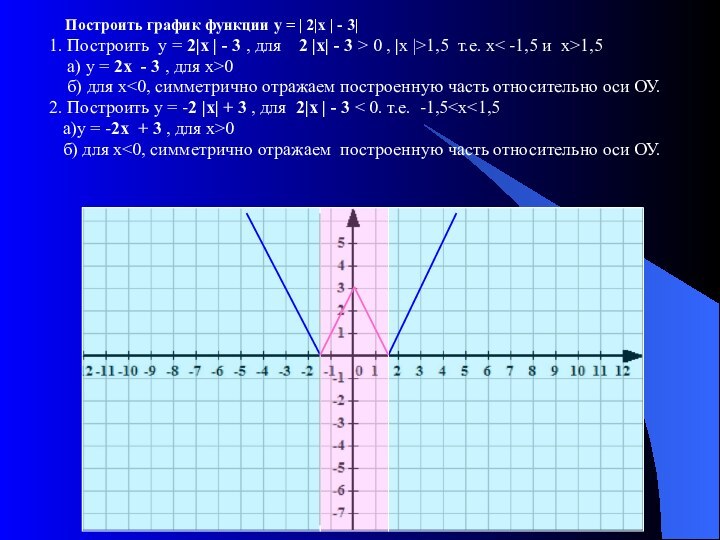
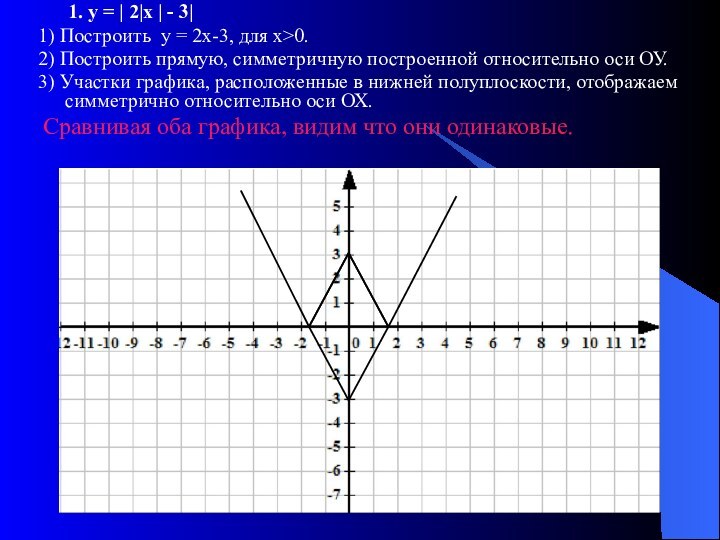
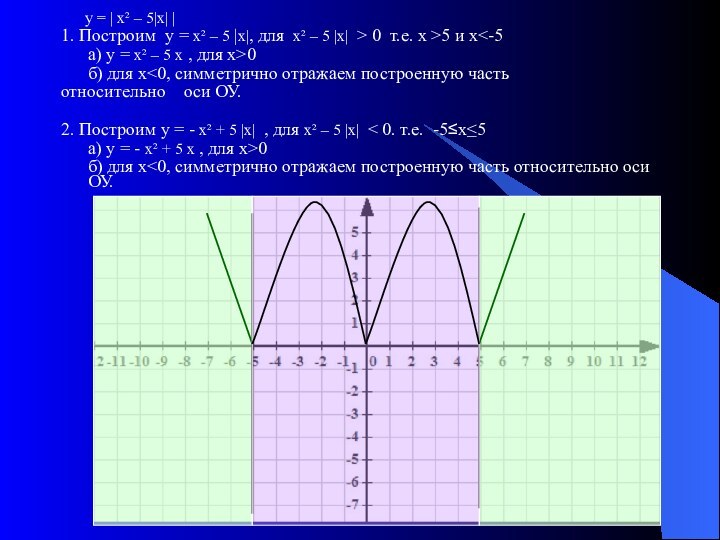
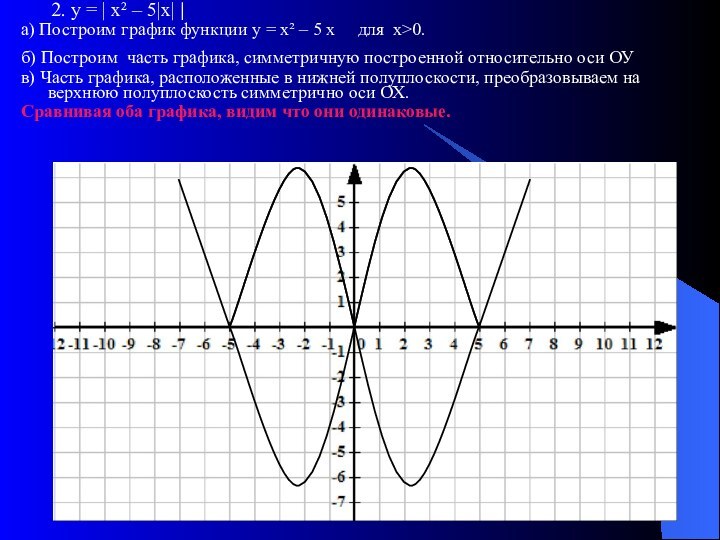
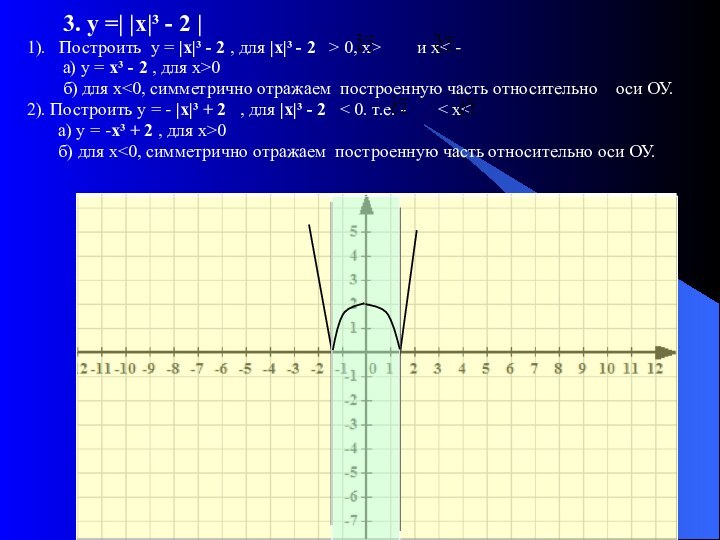
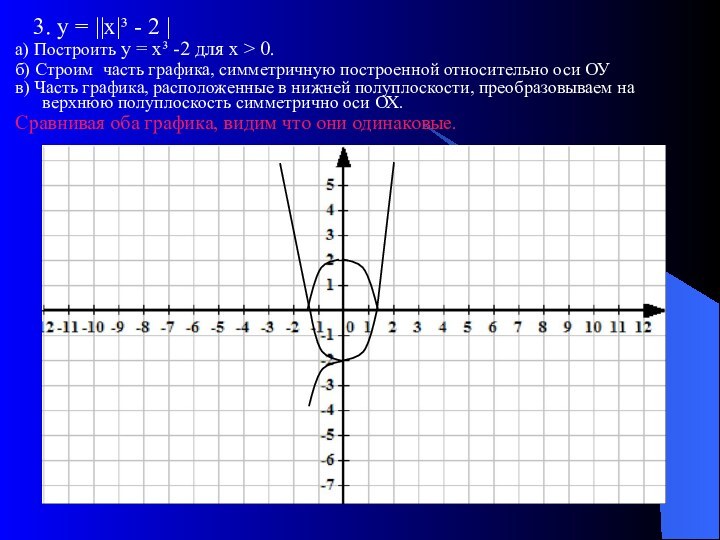
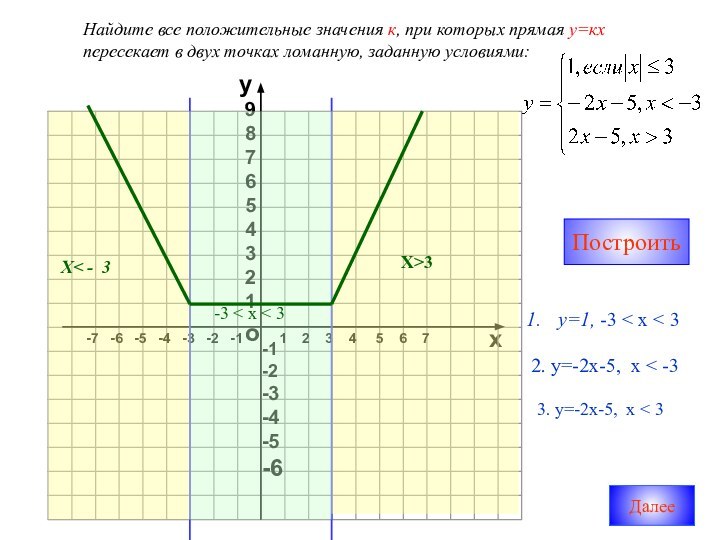
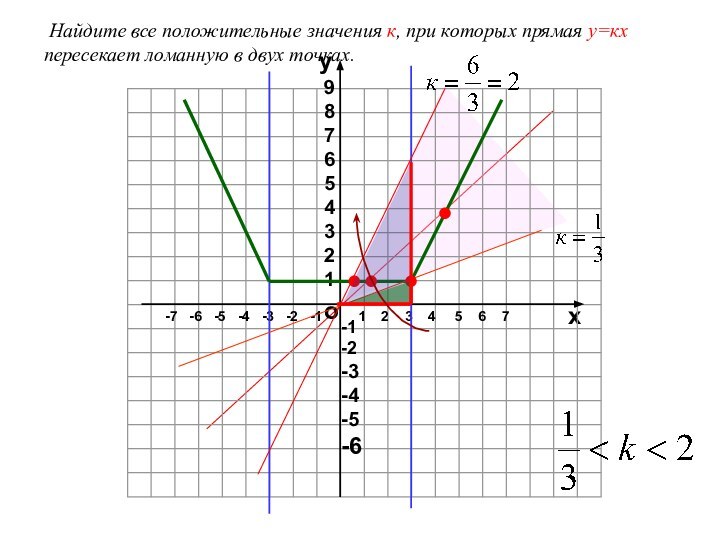
График функции у

= |х|
а) Если х≥0, то |х| = х функция у = х, т.е. график
совпадает с биссектрисой первого координатного угла.
б) Если х<0, то |х| = -х и у = - х. При отрицательных
значениях аргумента х график данной функции – прямая
у = -х, т.е. биссектриса второго координатного угла.

Построить

Далее

-3.

1) Поскольку |х| = х при х≥0, требуемый

график совпадает с
параболой у=0,25 х² - х - 3.
Если х<0, то поскольку х² = |х|², |х|=-х
и требуемый график совпадает с параболой у=0,25 х² + х - 3.

2) Если рассмотрим график у=0,25 х² - х - 3 при х≥0 и
отобразить его относительно оси ОУ мы получим тот же
самый график.

Построить

Далее

достаточно:
1. построить график функции у = f(х) для

х>0;
2. Для х<0, симметрично отразить построенную часть
относительно оси ОУ.

f |(х)|

у =х² - х -6

2. Участки графика, расположенные в

нижней полуплоскости, отображаем симметрично относительно оси ОХ.

Далее

достаточно:
1.Построить график функции у = f(х) ;
2. На участках,

где график расположен в нижней полуплоскости, т.е., где
f(х) <0, симметрично отражаем относительно оси абсцисс.

2|х | - 3|
1. Построить у = 2|х |

- 3 , для 2 |х| - 3 > 0 , |х |>1,5 т.е. х< -1,5 и х>1,5
а) у = 2х - 3 , для х>0
б) для х<0, симметрично отражаем построенную часть относительно оси ОУ.
2. Построить у = -2 |х| + 3 , для 2|х | - 3 < 0. т.е. -1,5<х<1,5
а)у = -2х + 3 , для х>0
б) для х<0, симметрично отражаем построенную часть относительно оси ОУ.

| - 3|
1) Построить у = 2х-3, для х>0.

2) Построить прямую, симметричную построенной относительно оси ОУ.
3) Участки графика, расположенные в нижней полуплоскости, отображаем симметрично относительно оси ОХ.
Сравнивая оба графика, видим что они одинаковые.

5|х| |
1. Построим у = х² – 5 |х|,

для х² – 5 |х| > 0 т.е. х >5 и х<-5
а) у = х² – 5 х , для х>0
б) для х<0, симметрично отражаем построенную часть
относительно оси ОУ.

2. Построим у = - х² + 5 |х| , для х² – 5 |х| < 0. т.е. -5≤х≤5
а) у = - х² + 5 х , для х>0
б) для х<0, симметрично отражаем построенную часть относительно оси ОУ.

– 5|х| |
а) Построим график функции у = х²

– 5 х для х>0.
б) Построим часть графика, симметричную построенной относительно оси ОУ
в) Часть графика, расположенные в нижней полуплоскости, преобразовываем на верхнюю полуплоскость симметрично оси ОХ.
Сравнивая оба графика, видим что они одинаковые.

2 |
1). Построить у = |х|³ - 2

, для |х|³ - 2 > 0, x> и x< -
а) у = х³ - 2 , для х>0
б) для х<0, симметрично отражаем построенную часть относительно оси ОУ.
2). Построить у = - |х|³ + 2 , для |х|³ - 2 < 0. т.е. - < x<
а) у = -х³ + 2 , для х>0
б) для х<0, симметрично отражаем построенную часть относительно оси ОУ.

|
а) Построить у = х³ -2 для х >

0.
б) Строим часть графика, симметричную построенной относительно оси ОУ
в) Часть графика, расположенные в нижней полуплоскости, преобразовываем на верхнюю полуплоскость симметрично оси ОХ.
Сравнивая оба графика, видим что они одинаковые.

у=кх пересекает в двух точках ломанную, заданную условиями:






Х>3
Х< -

3

-3 < x < 3

Построить

у=1, -3 < x < 3

2. у=-2х-5, x < -3

3. у=-2х-5, x < 3

Далее

прямая у=кх пересекает ломанную в двух точках.