Презентация на тему Математические модели

информационного моделирования в науке является язык математики.
Модели, построенные

с использованием математических понятий и формул, называются математическими моделями.

Математическая модель - информационная модель, в которой параметры и зависимости между ними выражены в математической форме.

v - скорость
t - время,
представляет

собой модель равномерного движения, выраженную в математической форме.

наклонной плоскости с ускорением a под воздействием силы F,

Ньютон получил соотношение F = mа.

Это математическая модель физической системы.

решению практических задач. Понятия числа, геометрической фигуры, уравнения, являются

примерами математических моделей.
К методу математического моделирования в учебном процессе приходится прибегать при решении любой задачи с практическим содержанием. Чтобы решить такую задачу математическими средствами, ее необходимо вначале перевести на язык математики (построить математическую модель).

Математическое моделирование

модели, сформулированной на языке математики.
Пример: нужно определить площадь поверхности

стола. Измеряют длину и ширину стола, а затем перемножают полученные числа. Это фактически означает, что реальный объект – поверхность стола – заменяется абстрактной математической моделью прямоугольником. Площадь этого прямоугольника и считается искомой.
Из всех свойств стола выделили три: форма поверхности (прямоугольник) и длины двух сторон. Не важны ни цвет стола, ни материал, из которого он сделан, ни то, как он используется.
Предположив, что поверхность стола – прямоугольник, легко указать исходные данные и результат. Они связаны соотношением S=ab.

модели.
Через иллюминатор затонувшего корабля требуется вытащить сундук с

драгоценностями. Даны некоторые предположения о формах сундука и окнах иллюминатора и исходные данные решения задачи.
Предположения: Иллюминатор имеет форму круга. Сундук имеет форму прямоугольного параллелепипеда.
Исходные данные: D - диаметр иллюминатора; x - длина сундука; y - ширина сундука; z - высота сундука.
Конечный результат: Сообщение: можно или нельзя вытащить.

, то сундук можно вытащить, а если

, то нельзя.

Системный анализ условия задачи выявил связи между размером иллюминатора и размерами сундука, учитывая их формы. Полученная в результате анализа информация отобразилась в формулах и соотношениях между ними, так возникла математическая модель.
Математической моделью решения этой задачи являются следующие зависимости между исходными данными и результатом:

спортивном зале.
   
Для решения задачи нужно знать площадь пола.

Для выполнения этого задания измеряют длину, ширину пола и вычисляют его площадь. Реальный объект – пол зала – занимается прямоугольником, для которого площадь является произведением длины на ширину. При покупке краски выясняют, какую площадь можно покрыть содержимым одной банки, и вычисляют необходимое количество банок.
Пусть A – длина пола,   B  - ширина пола, S1  - площадь, которую можно покрыть содержимым одной банки, N – количество банок.
Площадь пола вычисляем по формуле S=A×B, а количество банок, необходимых для покраски зала, N= A×B/S1.

часов, через вторую трубу – за 20 часов. За

сколько часов бассейн наполнится через две трубы?
Решение:
Обозначим время заполнения бассейна через первую и вторую трубу А и В соответственно. Примем за 1 весь объём бассейна, искомое время обозначим через t.
Так как через первую трубу бассейн наполняется за А часов, то 1/А –часть бассейна, наполняемая первой трубой за 1 час; 1/В - часть бассейна, наполняемая второй трубой за 1 час.
Следовательно, скорость наполнения бассейна первой и второй трубами вместе составит: 1/А+1/В.
Можно записать: (1/А+1/В)t=1. получили математическую модель, описывающую процесс наполнения бассейна из двух труб.
Искомое время можно вычислить по формуле:

удалённые друг от друга на 20 км. Мотоциклист выехал

из пункта В в направлении, противоположном А со скоростью 50 км/ч.
Составим математическую модель, описывающую положение мотоциклиста относительно пункта А через t часов.
За t часов мотоциклист проедет 50t км и будет находится от А на расстоянии 50t км + 20 км. Если обозначить буквой s расстояние (в километрах) мотоциклиста до пункта А, то зависимость этого расстояния от времени движения можно выразить формулой: S=50t + 20, где t>0.

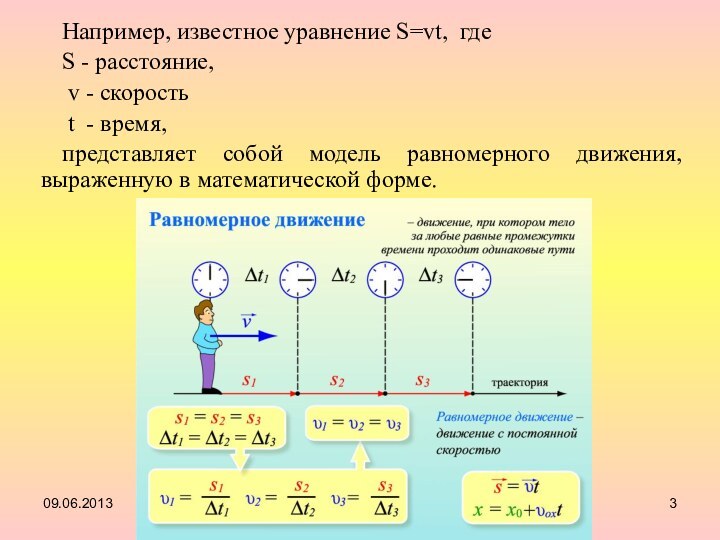
больше первого. Известно, что 1/5 первого числа равна 1/4

второго.

Составьте математические модели данных ситуаций:

У Миши x марок, а у Андрея в полтора раз больше. Если Миша отдаст Андрею 8 марок, то у Андрея станет марок вдвое больше, чем останется у Миши.

Во втором цехе работают x человек, в первом – в 4 раза больше, чем во втором, а в третьем - на 50 человек больше, чем во втором. Всего в трех цехах завода работают 470 человек.

Проверим:

Математической моделью решения этой задачи являются следующие зависимости между исходными данными и результатом: было у Миши х марок; у Андрея 1,5х. Стало у Миши х-8, у Андрея 1,5х+8. По условию задачи 1,5х+8=2(х-8).

Математической моделью решения этой задачи являются следующие зависимости между исходными данными и результатом: во втором цехе работают x человек, в первом – 4х, а в третьем - х+50. х+4х+х+50=470.

Математической моделью решения этой задачи являются следующие зависимости между исходными данными и результатом: первое число х; второе х+2,5. По условию задачи х/5=(х+2,5)/4.

Математические модели бывают не только алгебраические (в виде равенства

с переменными, как в разобранных выше примерах), но и в другом виде: табличные, графические и другие.
С другими видами моделей мы познакомимся на следующем занятии.

3, 4 (стр. 57) в тетради