полезно не упускать случаев делать его немного занимательным.
Великий французский математик, физик, философ Блез ПаскальЦель:
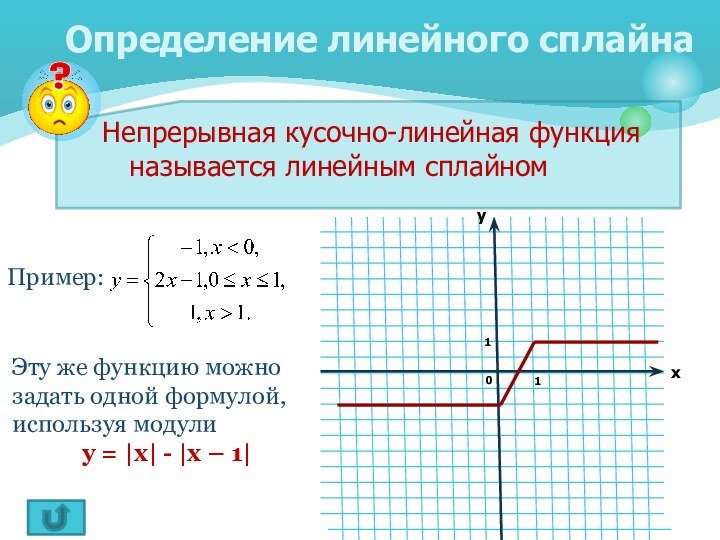
освоить метод линейного сплайна для построения графиков, содержащих модуль;
научиться применять его в простых ситуациях.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть








Цель:
освоить метод линейного сплайна для построения графиков, содержащих модуль;
научиться применять его в простых ситуациях.
ВВЕДЕНИЕ
Определение модуля
Модулем числа а называется расстояние (в единичных отрезках) от начала координат до точки А (а).
Это определение раскрывает геометрический смысл модуля.
Модулем (абсолютной величиной) действительного числа а называется то самое число а ≥ 0, и противоположное число –а, если а<0.
|a|?
0
а
А
х
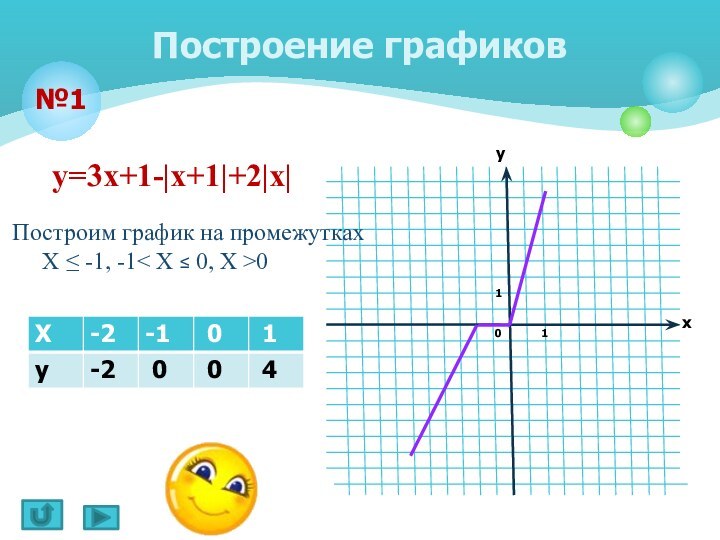
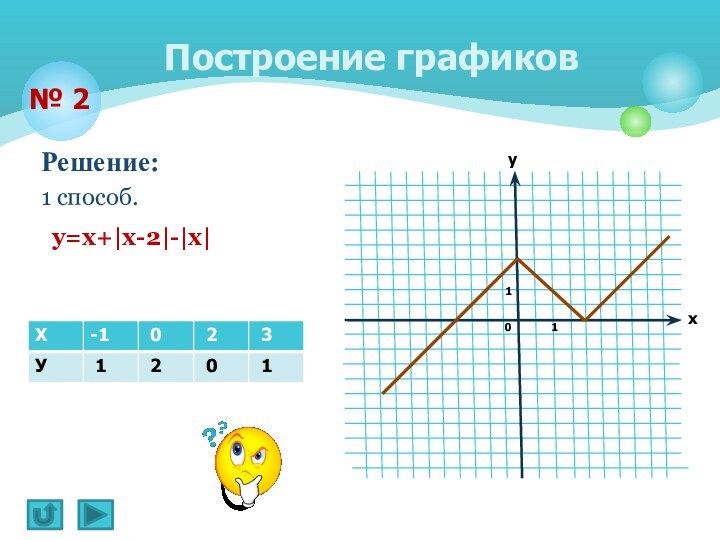
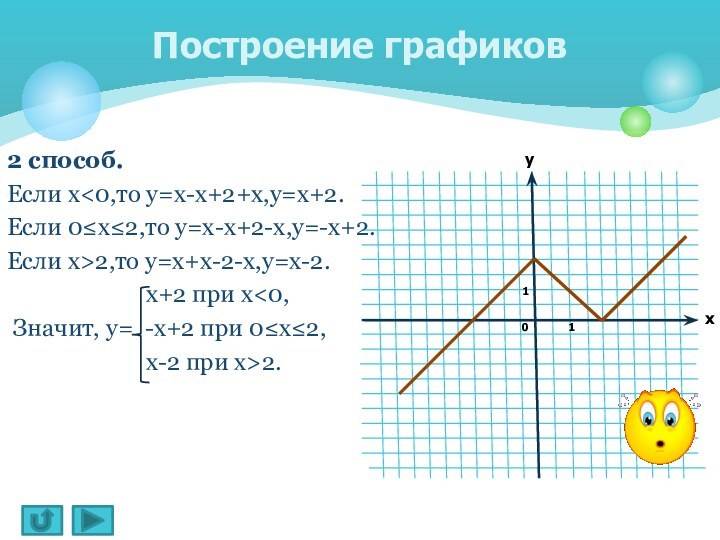
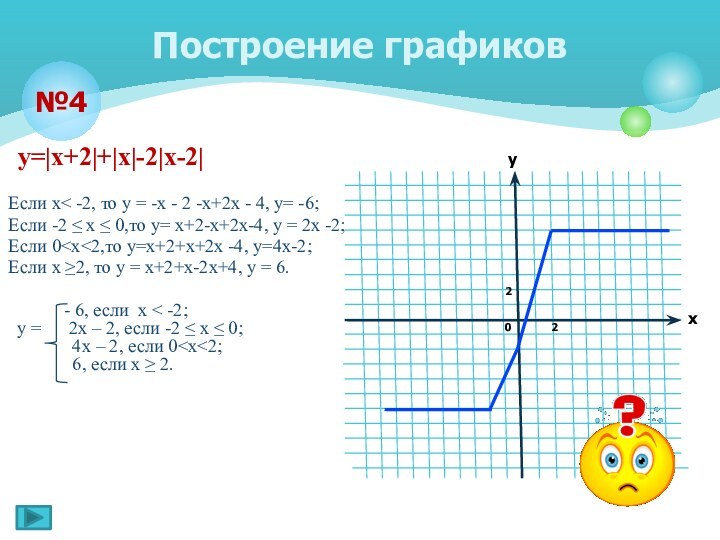
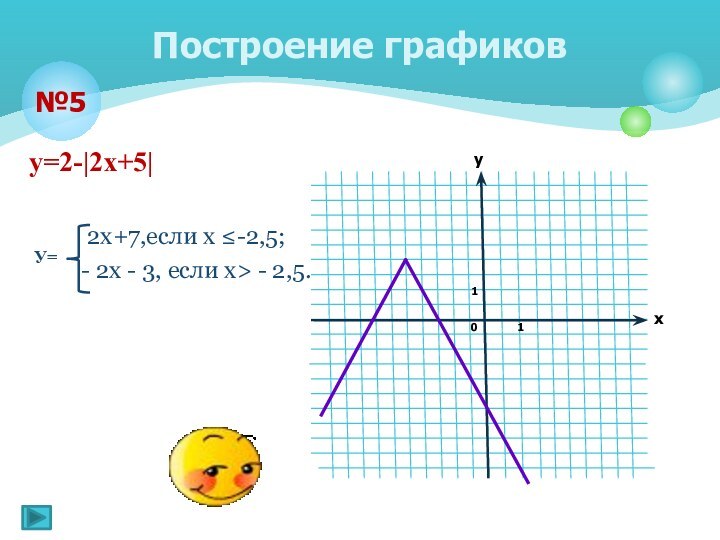
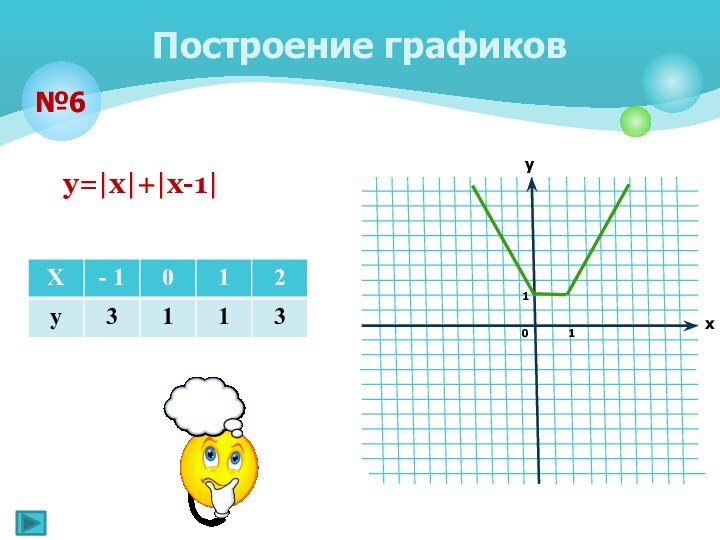
Построение графиков
№4
Заключение