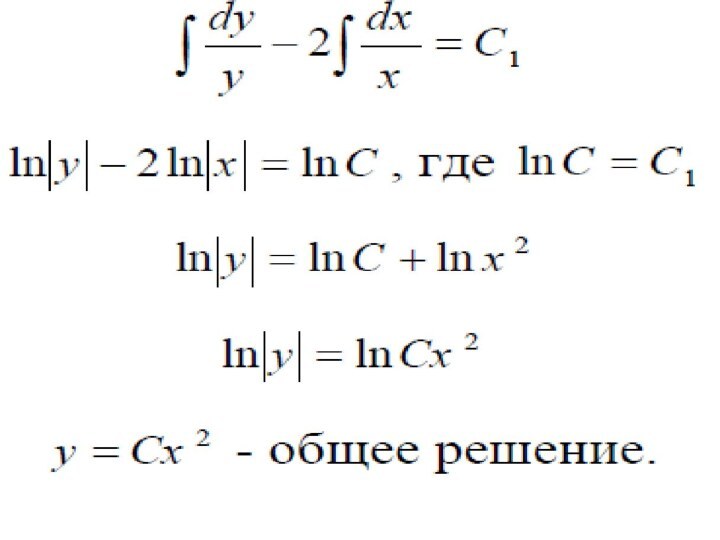Слайд 5
Пример. Размножение бактерий
Обозначим через x = x (t
) массу всех бактерий в момент времени t, тогда
dx/dt будет скоростью размножения этих бактерий. Cкорость размножения пропорциональна количеству бактерий, то существует постоянная k > 0 такая, что dx/dt=kt.
Легко проверить, что функция
вида , где С – некоторая постоянная
является решением уравнения .
Слайд 6
Дифференциальные уравнения первого порядка.
Уравнения разделяющимися переменными
Дифференциальное уравнение
первого порядка имеет вид
F(x , y, y′) = 0
.
Если это уравнение разрешено относительно y′ , то это уравнение имеет вид:
y′ = f (x , y) или dy=f (x , y)dx
Общим решением уравнения будет функция y=y(x ,C), зависящая от х и от одной произвольной постоянной, и обращающая это уравнение в тождество.
Слайд 7
Частным решением уравнения будет решение y = y(
x ,C0 ), полученное из общего при фиксированном значении
С, удовлетворяющее заданным начальным условиям: y = y0 при x = x0. Другими словами: найти интегральную кривую уравнения, проходящую через заданную точку M0 (x0,y0 ).
Дифференциальное уравнение вида
P1 (x)Q1(y)dx+P2(x)Q 2 (y) dy =0,
где P1 (x ), P2 (x ) – функции только от х, а Q1(y), Q2(y) – функции только от у, называется уравнением с разделяющимися переменными.
Слайд 8
Делением обеих частей уравнения на произведение Q1 (y)P2
(x ) может быть приведено к уравнению с разделенными
переменными:
Общим интегралом уравнения будет:
Слайд 9
Пример . Решить уравнение:
(1+ x )ydx + (1−
y)xdy = 0 .
Разделив обе части уравнения на произведение
ху, получим уравнение с
разделенными переменными:
Интегрируя, находим общий интеграл:
Слайд 10
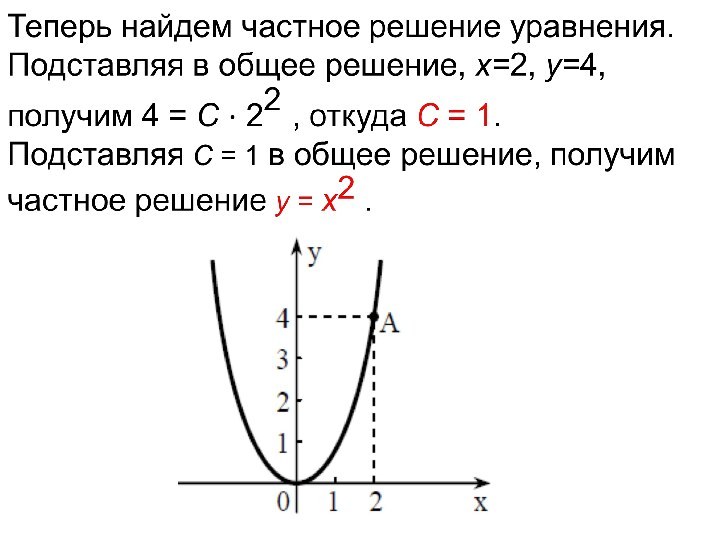
Пример. Дано уравнение xy′ − 2y = 0.
Найти частное решение этого уравнения, удовлетворяющее начальному условию y
= 4 при x = 2 .
Урвнение имеет вид:
Разделяя переменные, получим:
Интегрируем:
Слайд 13
Дифференциальные уравнения второго порядка
Общим решением уравнения будет функция
y=y(x,C1,C2 ) , зависящая от x и от двух
произвольных независимых постоянных C1 и C2, обращающая данное уравнение в тождество.
Частное решение уравнения имеет вид
– фиксированные постоянные .
Слайд 14
Постоянные определяются из системы уравнений:
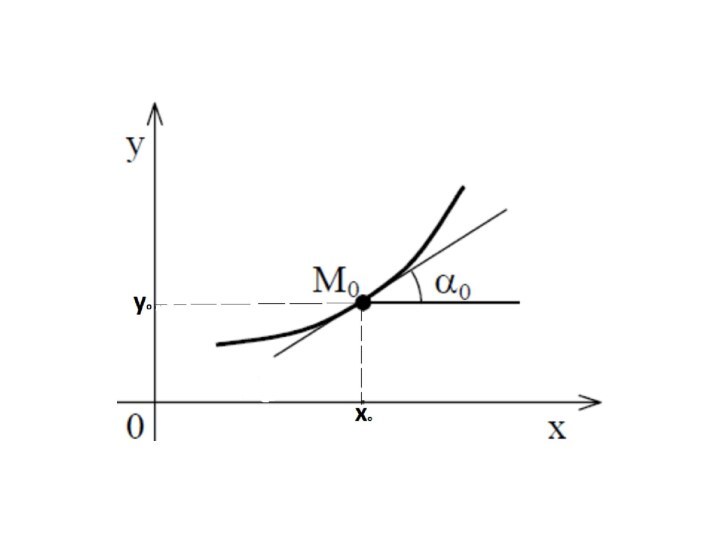
Геометрически это означает, что
ищется интегральная кривая, которая проходит через точку M0(x0y0) и
имеет в этой точке заданную
касательную, образующую с осью Oх такой угол α0 , что tgα0 = y′0
Слайд 16
Дифференциальные уравнения второго порядка, допускающие понижение порядка
Уравнение вида
y′′ = f (x ) решается последовательным двукратным интегрированием
правой части, причем при каждом интегрировании получается одна произвольная постоянная; окончательное решение содержит две произвольных
постоянных:
Слайд 17
Пример . Решить уравнение y′′ = x +
sin x
Слайд 18
Однородные линейные дифференциальные уравнения
второго порядка с постоянными коэффициентами
Слайд 21
Теория вероятностей.
Определения:
Событием называется всякий факт, который может
произойти или не произойти в результате опыта;
События называются несовместными,
если появление одного из них исключает появление других. Классическим примером несовместных событий является результат подбрасывания монеты – выпадение лицевой стороны монеты исключает выпадение обратной стороны (в одном и том же опыте);
Слайд 22
Полной группой событий называется совокупность всех возможных результатов
опыта;
Достоверным событием называется событие, которое наверняка произойдет в результате
опыта. Событие называется невозможным, если оно никогда не произойдет в результате опыта. Например, если из коробки, содержащей только красные и зеленые шары, наугад вынимают один шар, то появление среди вынутых шаров белого – невозможное событие. Появление красного и появление зеленого шаров образуют полную группу событий.
Слайд 23
Вероятностью события А называется математическая оценка возможности появления
этого события в результате опыта. Вероятность события А равна
отношению числа, благоприятствующих событию А исходов опыта к общему числу попарно несовместных исходов опыта, образующих полную группу событий.
Очевидно, что вероятность достоверного события равна единице, а вероятность невозможного – равна нулю. Таким образом, значение вероятности любого события – есть положительное число, заключенное между нулем и единицей.
Слайд 24
Пример. В коробке находится 10 шаров. 3 из
них красные, 2 – зеленые, остальные белые. Найти вероятность
того, что вынутый наугад шар будет красным, зеленым или белым.
Появление красного, зеленого и белого шаров составляют полную группу событий. Обозначим появление красного шара - событие А, появление зеленого - событие В, появление белого –С.
Тогда в соответствием с записанными выше формулами получаем:
Слайд 25
Относительной частотой события А называется отношение числа опытов,
в результате которых произошло событие А к общему числу
опытов.
Отличие относительной частоты от вероятности заключается в том, что вероятность вычисляется без непосредственного произведения опытов, а относительная частота – после опыта.
Так в рассмотренном выше примере, если из коробки наугад извлечено 5 шаров и 2 из них оказались красными, то относительная частота появления красного шара равна:
Слайд 26
Теорема (сложения вероятностей). Вероятность суммы двух несовместных событий
равна сумме вероятностей этих событий
P(A+B)=P(A)+P(B)
Следствие 1: Если события образуют
полную группу несовместных событий, то сумма их вероятностей равна единице.
Следствие 2: Сумма вероятностей противоположных событий равна единице.
Слайд 27
Теорема. (Умножения вероятностей) Вероятность произведения двух событий (совместного
появления этих событий) равна произведению вероятности одного из них
на условную вероятность другого, вычисленную при условии, что первое событие уже наступило.
Если события независимые, то, и теорема умножения вероятностей принимает вид:
P(AB)=P(A)P(B).