Презентация на тему Методы решений заданий С5. Метод областей в решении задач

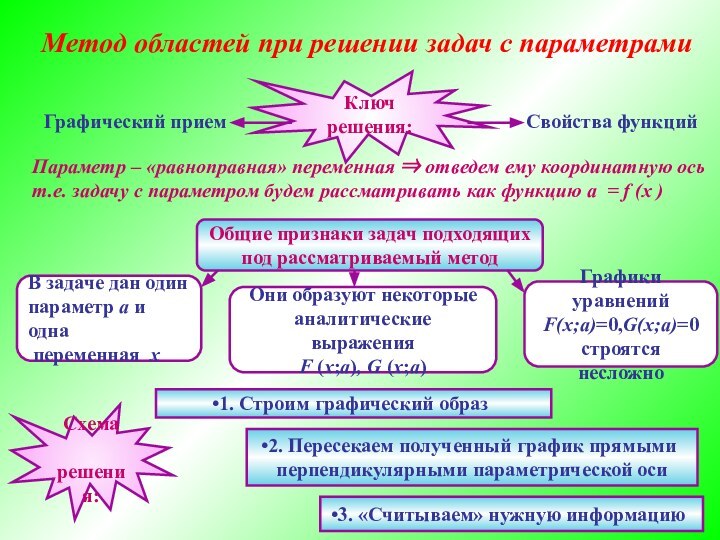
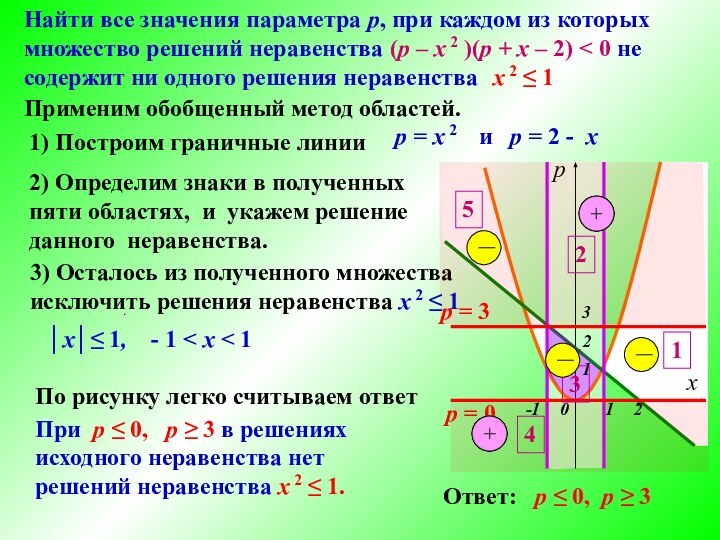
определения
2. Граничные линии
3. Координатная плоскость
4. Знаки в областях
5.Ответ по

1. Область определения
2. Корни
3. Ось
4. Знаки на интервалах
5. Ответ.

Метод интервалов:

Метод областей:

Обобщённый метод областей

х – у = 0 (у = х) и

При х = 1, у = 0 левая часть неравенства равна -1(отрицательна)

Ответ: заштрихованные области на рисунке удовлетворяют условию (х – у) (х у –1) ≥ 0

х

у

0

1

- 1

- 1

1

На координатной плоскости изобразите множество точек , координаты которых удовлетворяют неравенству(х – у) (х у –1) ≥ 0

1

2

3

4

5

6

Следовательно, в 1 области, содержащей точку (1; 0), левая часть неравенства имеет знак минус, а в остальных областях её знаки чередуются.

Пример для понимания «метода областей»

1
- 1
1
1
х
у
0
На координатной плоскости изобразите множество точек, удовлетворяющих неравенству

Ответ: заштрихованные области
на рисунке.

Область определения неравенства:

Проводим граничные линии, с учётом области определения

Определяем знаки на областях подстановкой в отдельных точках

Пример для понимания «метода областей»

прием
Свойства функций
Параметр – «равноправная» переменная ⇒ отведем ему координатную

Общие признаки задач подходящих
под рассматриваемый метод

В задаче дан один
параметр а и одна
переменная х

Они образуют некоторые
аналитические выражения
F (x;a), G (x;a)

Графики уравнений
F(x;a)=0,G(x;a)=0
строятся несложно

1. Строим графический образ

2. Пересекаем полученный график прямыми
перпендикулярными параметрической оси

3. «Считываем» нужную информацию

Схема
решения:

которых
множество решений неравенства (р – х 2 )(р +

.

Применим обобщенный метод областей.

2) Определим знаки в полученных пяти областях, и укажем решение данного неравенства.

3) Осталось из полученного множества
исключить решения неравенства х 2 ≤ 1

По рисунку легко считываем ответ

Ответ: р ≤ 0, р ≥ 3

1) Построим граничные линии

р = 3

р = 0

0

2

2

-1

1

3

1

р = х 2 и р = 2 - х

При р ≤ 0, р ≥ 3 в решениях исходного неравенства нет решений неравенства х 2 ≤ 1.

1

2

3

4

5

│x│≤ 1, - 1 < x < 1

а?






2
-2
2
-2
1
-1
1

Графиком второго уравнения является неподвижная окружность с центром

4 решения при а = 1

Ответ:

решений нет, если

8 решений, если

4 решения, если

0

имеет ровно четыре решения?

Второе уравнение задает семейство окружностей с центром (2;0) и радиусом а.

0

1, при пересечении параболы с горизонтальной прямой . По

5 ≤ а ≤ 12

Пусть сos 2 x + 1= t; t ϵ [1; 2];

тогда уравнение примет вид

При каких значениях параметра а сумма log a (cos 2 x + 1) и log a (cos 2 x + 5) равна 1 хотя бы при одном значении х?

log a (cos 2 x + 1) + log a (cos 2 x + 5) = 1;

заметим, 0 ≤ cos 2 x ≤ 1

log a (t∙(t + 4)) = 1; откуда

t 2 + 4t = a

у = а

у = а

Ответ: при всех a ∈ [5;12]

количество их общих точек.
х
у














2
-2

3
3
1
5

А
В
С
О
Найдите все значения параметра а,