Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Методика первоначального ознакомления с действием умножения.Методика ознакомления с названиями чисел при умножении и зависимость между ними.

Содержание

2. Необходимость введения нового действия осознается учащимися в
5. Они самостоятельно приходят к выводу, что достаточно
6. УмножениеОпределяя умножение как сложение одинаковых слагаемых и
7. Для усвоения учащимися смысла умножения можно использовать
8. Так же, как и при сложении, полезно
9. Затем вводятся названия компонентов при умножении : множитель
10. Составляется пример на умножение, записывается широко на
11. По данному примеру на умножение составляются 2
12. Дети называют числа так, как они назывались
13. Теперь зависимость дети могут увидеть сами: если
14. Для обоснования частных случаев вида 1 ∙ а
15. Методика обучения решению простых задач на умножение
16. При этом можно использовать наглядность: «Положите в
17. В этом случае говорят: кругов в 2
18. Дети не могут не видеть, что смысл
19. На этом же уроке вводится текстовая задача:
20. Выбор действия: «Если сказано в 3 раза
21. В некоторых образовательных направлениях («Школа 2000», «Нач.
22. Ребенок должен понимать обратную связь: если зеленых
23. Смысл отношения «меньше в…» связан с делением
24. Смысл отношения «меньше в…» связан с
25. Следует иметь ввиду, что прочное сравнение двух
26. Рассмотрим, например, такую ситуацию: «У Коли 10
27. Раскрытие смысла деления и методика изучения зависимости
28. Выбор подхода обусловлен тем, что он позволяет
30. Он сводится к разбиению конечного множества яблок
31. Доступно им и такое задание: «Раздай 10
32. Процесс деления на равные части довольно трудно
33. Таким образом, частное может обозначать число частей,
34. В практике начального обучения принято сначала рассматривать
35. Например, по-русски не говорят «10 яблок разделить
36. При изучении зависимости между компонентами деления можно
37. Затем учитель предлагает детям составить еще один
38. Под руководством учителя дети делают вывод: если
39. Частные случаи деления с 1 и 0
40. Рассуждение: разделить 3 на 1 – значит,
41. Скачать презентацию
42. Похожие презентации

Необходимость введения нового действия осознается учащимися в процессе рассмотрения различных ситуаций. Например, учащимся предлагается схематический чертёж поля прямоугольной формы, которое разбито на равные участки (квадраты). Нужно определить, на сколько участков (квадратов) разбито данное поле

Главная
Математика
Презентация Методика первоначального ознакомления с действием умножения.Методика ознакомления с названиями чисел при умножении и зависимость между ними.

Методика первоначального ознакомления с действием умножения. Методика ознакомления с

Необходимость введения нового действия осознается учащимися в процессе рассмотрения различных ситуаций. Например,

Презентация Методика первоначального ознакомления с действием умножения.Методика ознакомления с названиями чисел при умножении и зависимость между ними.

Они самостоятельно приходят к выводу, что достаточно посчитать число квадратов в одном

УмножениеОпределяя умножение как сложение одинаковых слагаемых и показывая новую математическую запись, учитель,

Для усвоения учащимися смысла умножения можно использовать упражнения:а) выполнение рисунка по данной

Так же, как и при сложении, полезно при разъяснении смысла умножения предлагать

Затем вводятся названия компонентов при умножении : множитель множитель произведение 8 • 4

Составляется пример на умножение, записывается широко на доске: 3 • 2 = 6

По данному примеру на умножение составляются 2 примера на деление: 6 : 2

Дети называют числа так, как они назывались в первом примере, учитель крепит

Теперь зависимость дети могут увидеть сами: если произведение двух чисел разделить на

Для обоснования частных случаев вида 1 ∙ а и 0 ∙ а детям предлагается

Методика обучения решению простых задач на умножение и деление, в которых задано

При этом можно использовать наглядность: «Положите в первый ряд 4 треугольника. Ниже

В этом случае говорят: кругов в 2 раза больше, чем треугольников, а

Дети не могут не видеть, что смысл отношения «больше в несколько раз»

На этом же уроке вводится текстовая задача: « Для детского сада купили

Выбор действия: «Если сказано в 3 раза больше, то каким действием будем

В некоторых образовательных направлениях («Школа 2000», «Нач. школа XXI век») одновременно с

Ребенок должен понимать обратную связь: если зеленых мячей в 3 раза меньше,

Смысл отношения «меньше в…» связан с делением на равные части. «В первом

Смысл отношения «меньше в…» связан с делением на равные части. «В

Следует иметь ввиду, что прочное сравнение двух чисел, связанное с ответом на

Рассмотрим, например, такую ситуацию: «У Коли 10 тетрадей, у Пети - 2.

Раскрытие смысла деления и методика изучения зависимости между числами при делении. Частные

Выбор подхода обусловлен тем, что он позволяет опирать на жизненный опыт ребёнка

Он сводится к разбиению конечного множества яблок на равночисленные множества (по 2

Доступно им и такое задание: «Раздай 10 яблок поровну двум девочкам. Сколько

Процесс деления на равные части довольно трудно изобразить на рисунке, но когда

Таким образом, частное может обозначать число частей, на которое разделили данное количество

В практике начального обучения принято сначала рассматривать ситуации, связанные только с первым

Например, по-русски не говорят «10 яблок разделить на 2 яблока», говорят так

При изучении зависимости между компонентами деления можно использовать подвижные карточки. Сначала составляется

Затем учитель предлагает детям составить еще один пример на деление и на

Под руководством учителя дети делают вывод: если делимое разделить на частное, получится

Частные случаи деления с 1 и 0 основываются на взаимосвязи деления и

Рассуждение: разделить 3 на 1 – значит, найти такое число, при умножении

0:2=0, так как 0*2=0;0:8=0, так как 0*8=0 Вывод: при делении нуля на

Слайды презентации

Слайд 2 Необходимость введения нового действия осознается учащимися в процессе

Необходимость введения нового действия осознается учащимися в процессе рассмотрения различных ситуаций.

рассмотрения различных ситуаций. Например, учащимся предлагается схематический чертёж поля

прямоугольной формы, которое разбито на равные участки (квадраты). Нужно определить, на сколько участков (квадратов) разбито данное поле

Слайд 3

Слайд 4

Слайд 5 Они самостоятельно приходят к выводу, что достаточно посчитать

Они самостоятельно приходят к выводу, что достаточно посчитать число квадратов в

число квадратов в одном ряду (их 11) и повторить

это число слагаемыми 4 раза (11+11+11+11). Можно также предложить ситуации с величинами: цена, кол-во, стоимость. Например: один батон стоит 10 р. Сколько нужно заплатить денег за 2 батона? (10+10). За три батона? (10+10+10). За 12 батонов (10+10+10+...). Такую длинную запись можно выполнить иначе: 10х12.

Слайд 6 Умножение
Определяя умножение как сложение одинаковых слагаемых и показывая

УмножениеОпределяя умножение как сложение одинаковых слагаемых и показывая новую математическую запись,

новую математическую запись, учитель, используя действия с предметами разъясняет

детям значение каждого числа в этой записи. Особенно важно обратить их внимание на то, что
число, на которое мы умножаем, показывает, сколько раз
первое число повторяется слагаемым.

Слайд 7 Для усвоения учащимися смысла умножения можно использовать упражнения:
а)

Для усвоения учащимися смысла умножения можно использовать упражнения:а) выполнение рисунка по

выполнение рисунка по данной математической записи
б) выполнение математической записи,

соответствующей рисунку
в) соотнесение математической записи и рисунка

Слайд 8 Так же, как и при сложении, полезно при

Так же, как и при сложении, полезно при разъяснении смысла умножения

разъяснении смысла умножения предлагать ученикам задания, в процессе выполнения

которых у них может возникнуть догадка о закономерности, связанной с переместительным свойством умножения.
    г) замена произведения суммой
     д) замена суммы произведением
     е) сравнение числовых выражений
     ж) сравнение двух произведений, значение одного из которых известно (Используя первое равенство, найдите значение второго произведения).

Слайд 9   Затем вводятся названия компонентов при умножении :

множитель            множитель

Затем вводятся названия компонентов при умножении : множитель множитель произведение 8

        произведение
            8        •          4           =         32

             произведение
и рассматривается зависимость между

ними. С этой целью можно использовать подвижные карточки.

Слайд 10 Составляется пример на умножение, записывается широко на доске:
3

Составляется пример на умножение, записывается широко на доске: 3 • 2 =

• 2 = 6
Учитель предлагает назвать компоненты умножения.

Появляются карточки:
3 • 2 = 6
множитель множитель произведение

Слайд 11 По данному примеру на умножение составляются 2 примера

По данному примеру на умножение составляются 2 примера на деление: 6 :

на деление:

6 : 2 = 3

6

: 3 = 2

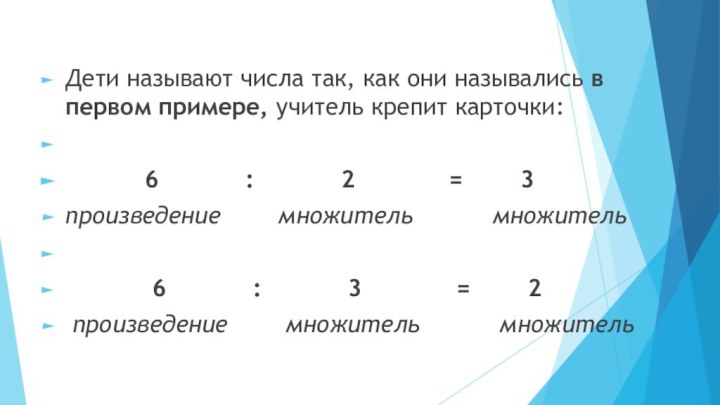
Слайд 12 Дети называют числа так, как они назывались в

Дети называют числа так, как они назывались в первом примере, учитель

первом примере, учитель крепит карточки:

6            :            2             =     3
произведение        множитель           множитель

6            :            3             =        2
произведение        множитель           множитель

Слайд 13 Теперь зависимость дети могут увидеть сами:
если произведение

Теперь зависимость дети могут увидеть сами: если произведение двух чисел разделить

двух чисел разделить на один из множителей, то получим

другой множитель.

Слайд 14 Для обоснования частных случаев вида 1 ∙ а и

Для обоснования частных случаев вида 1 ∙ а и 0 ∙ а детям

0 ∙ а детям предлагается задание:
Найди результат, пользуясь сложением:

   1 ∙ 2,   1 ∙ 3,   1 ∙ 4,   1 ∙ 6,   1 ∙ 7
   0 ∙ 2,   0 ∙ 6,   0 ∙ 3,   0 ∙ 5
После выполнения задания делается вывод.
Случаи а ∙ 1, а ∙ 0 запоминаются (так договорились), так как   их нельзя объяснить, используя конкретный смысл умножения (нет повторяемости слагаемых)

Слайд 15 Методика обучения решению простых задач на умножение и

Методика обучения решению простых задач на умножение и деление, в которых

деление, в которых задано отношение «больше в…», «меньше в…»
При

введении любой задачи выделяется три этапа:
подготовительный,
ознакомление,
закрепление.
Перед рассмотрением задачи на увеличение в несколько раз дети знакомятся со смыслом отношения «больше в…».

Слайд 16 При этом можно использовать наглядность: «Положите в первый

При этом можно использовать наглядность: «Положите в первый ряд 4 треугольника.

ряд 4 треугольника. Ниже положите 2 раза по столько

кругов, сколько треугольников в первом ряду.

Слайд 17 В этом случае говорят:
кругов в 2 раза

В этом случае говорят: кругов в 2 раза больше, чем треугольников,

больше, чем треугольников, а
треугольников в 2 раза меньше,

чем кругов».

Слайд 18 Дети не могут не видеть, что смысл отношения

Дети не могут не видеть, что смысл отношения «больше в несколько

«больше в несколько раз» тесно связан с умножением:

совокупность

предметов увеличивается, мы 4 кружка повторяем 2 раза.

Делается вывод: если говорят «больше в …», надо умножить.

Слайд 19 На этом же уроке вводится текстовая задача: «

На этом же уроке вводится текстовая задача: « Для детского сада

Для детского сада купили 4 зеленых мяча, а красных

в 3 раза больше. Сколько красных мячей купили?»
З. – 4 м.
К. - ?, в 3 раза Б.

Слайд 20 Выбор действия: «Если сказано в 3 раза больше,

Выбор действия: «Если сказано в 3 раза больше, то каким действием

то каким действием будем решать?»
Решение записывается. Вместо традиционной краткой

записи можно использовать схему (отрезки).

Слайд 21 В некоторых образовательных направлениях («Школа 2000», «Нач. школа

В некоторых образовательных направлениях («Школа 2000», «Нач. школа XXI век») одновременно

XXI век») одновременно с задачей на увеличение в несколько

раз в прямой форме, вводится косвенная форма:
«Купили 4 зеленых мяча, это в 3 раза меньше, чем красных. Сколько красных мячей купили?»
З. – 4 м., в 3 раза М.
К. - ?

Слайд 22 Ребенок должен понимать обратную связь: если зеленых мячей

Ребенок должен понимать обратную связь: если зеленых мячей в 3 раза

в 3 раза меньше, то красных в 3 раза

больше. «Больше в…», значит, надо умножить.
Чтобы дети не путали задачи, связанные с отношениями «больше в…» и «больше на…» следует научить их при выборе действия ориентироваться на предлог: «на… больше» - значит выполняем сложение, «в…больше» - значит умножение. Решение задач этих видов следует перемежать.

Слайд 23 Смысл отношения «меньше в…» связан с делением на

равные части.
«В первом ряду 8 кружков, во второй

надо положить в 4 раза меньше»
Используется наглядность: чтобы получить в 4 раза меньше кружков, чем 8, разделим 8 кружков на 4 равные части и возьмем столько, сколько их в одной такой части. Дети подводятся к выводу: если говорится «меньше в…», выполняется деление. Работа над текстовой задачей аналогична предыдущему виду

Слайд 24
Смысл отношения «меньше в…» связан с делением

Смысл отношения «меньше в…» связан с делением на равные части.

на равные части.
«В первом ряду 8 кружков, во

второй надо положить в 4 раза меньше»
Используется наглядность: чтобы получить в 4 раза меньше кружков, чем 8, разделим 8 кружков на 4 равные части и возьмем столько, сколько их в одной такой части. Дети подводятся к выводу: если говорится «меньше в…», выполняется деление. Работа над текстовой задачей аналогична предыдущему виду

Смысл отношения «меньше в…» связан с делением на равные части.
«В первом ряду 8 кружков, во второй надо положить в 4 раза меньше»
Используется наглядность: чтобы получить в 4 раза меньше кружков, чем 8, разделим 8 кружков на 4 равные части и возьмем столько, сколько их в одной такой части. Дети подводятся к выводу: если говорится «меньше в…», выполняется деление. Работа над текстовой задачей аналогична предыдущему виду

Смысл отношения «меньше в…» связан с делением на равные части.
«В первом ряду 8 кружков, во второй надо положить в 4 раза меньше»
Используется наглядность: чтобы получить в 4 раза меньше кружков, чем 8, раздели 8 кружков на 4 равные части и возьмем столько, сколько их в одной такой части. Дети подводятся к выводу: если говорится «меньше в…», выполняется деление. Работа над текстовой задачей аналогична предыдущему виду

Слайд 25 Следует иметь ввиду, что прочное сравнение двух чисел,

Следует иметь ввиду, что прочное сравнение двух чисел, связанное с ответом

связанное с ответом на вопрос: «Во сколько раз одно число

больше (меньше) другого?» фактически сводится к делению по содержанию.

Слайд 26 Рассмотрим, например, такую ситуацию: «У Коли 10 тетрадей,

Рассмотрим, например, такую ситуацию: «У Коли 10 тетрадей, у Пети -

у Пети - 2. Во сколько раз у Коли

тетрадей больше, чем у Пети?»
Для того, чтобы ответить на этот вопрос, нужно узнать, сколько раз 2 содержится в 10. Для этого необходимо выполнить деление по содержанию: 10:2 = 5(раз).
Число 5 означает, что 2 содержится в 10 5 раз. Значит 10 больше 2 в 5 раз, и 2 меньше 10 в 5 раз.
Вывод: чтобы узнать, во сколько раз одно число больше или меньше другого, надо большее число разделить на меньшее.

Слайд 27 Раскрытие смысла деления и методика изучения зависимости между

Раскрытие смысла деления и методика изучения зависимости между числами при делении.

числами при делении. Частные случаи деления с 0 и

Основа формирования у младших школьников представлений о смысле деления - теоретико-множественный подход к трактовке частного, суть которого сводится к разбиению конечных множеств на равночисленные множества, не имеющих общих элементов

Слайд 28 Выбор подхода обусловлен тем, что он позволяет опирать

Выбор подхода обусловлен тем, что он позволяет опирать на жизненный опыт

на жизненный опыт ребёнка при введении новой терминологии и

математической записи. Действительно, большинство учащихся легко справляются с таким практическим заданием: «Раздай 10 яблок по 2 каждой девочке. Сколько девочек получат яблоки?».
Наглядное изображение выполняемых действий помогает ребенку осознать их математический смысл.

Слайд 29

Слайд 30 Он сводится к разбиению конечного множества яблок на

Он сводится к разбиению конечного множества яблок на равночисленные множества (по

равночисленные множества (по 2 яблока).
В результате - получаем

число частей в этом разбиении.
На языке, доступном младшему школьнику, это означает, что он разделил яблоки на части, по 2 в каждой, т.е. узнал, «сколько раз по 2 содержится в 10».
Выполненное действие в математике принято записывать так:
10 : 2 = 5 ( десять разделить на 2 - получится 5).

Слайд 31 Доступно им и такое задание: «Раздай 10 яблок

Доступно им и такое задание: «Раздай 10 яблок поровну двум девочкам.

поровну двум девочкам. Сколько яблок получит каждая?»
В данной ситуации

учащиеся могут действовать по-разному:
а) Одни будут брать по одному яблоку и раздавать их по очереди, сначала одной девочке, потом другой, пока не раздадут все яблоки.
б) Другие могут сразу взять 2 яблока, т.к. девочек две и разделить между ними эти яблоки, затем так же поступить со второй парой яблок, с третьей и т.д., пока все не раздадут.
В результате выполнения описанных действий множество всех яблок будет разделено на 2 равные части, численность каждой из которых равна 5.

Слайд 32 Процесс деления на равные части довольно трудно изобразить

Процесс деления на равные части довольно трудно изобразить на рисунке, но

на рисунке, но когда деление выполнено практически и определена

численность каждой части, рисунок можно использовать для того, чтобы учащиеся осознали результат выполненного предметного действия.

Слайд 33 Таким образом, частное может обозначать число частей, на

Таким образом, частное может обозначать число частей, на которое разделили данное

которое разделили данное количество яблок ( при этом делили

поровну, по 2 в каждой части ).
Этот случай деления в методике математики принято называть «делением по содержанию»,
но частное может обозначать количество яблок в каждой части (при этом делили опять же поровну, на 2 равные части).
Этот случай называют «делением на 2 равные части».

Слайд 34 В практике начального обучения принято сначала рассматривать ситуации,

В практике начального обучения принято сначала рассматривать ситуации, связанные только с

связанные только с первым случаем деления, затем уже со

вторым.
Некоторые учителя вводят даже термины «деление по содержанию» и «деление на равные части», требуя от школьников узнать каждый случай деления и назвать его, употребляя при этом соответствующие термины.
При этом, когда выполняется «деление по содержанию», требуется говорить, что «10 разделили по 2»,
когда выполняется «деление на равные части», требуется говорить, что «10 разделили на 2».
Но при чтении числовых равенств «10:2=5; 8:4 = 2) целесообразно пользоваться формулировкой (10 разделить на 2, 8 разделить на 4).
Термин «разделить по» употребляется тогда, когда речь идет о конкретных предметах и связан с особенностями русского языка.

Слайд 35 Например, по-русски не говорят «10 яблок разделить на

Например, по-русски не говорят «10 яблок разделить на 2 яблока», говорят

2 яблока», говорят так «10 яблок разделить по 2

яблока».
Так как при чтении числового равенства мы не называем предметы, поэтому можно сказать: «10 разделить на 2, получим 5».
Поэтому не следует вводить термины «деление по содержанию» и «деление на равные части», т.к. математический смысл одного и другого случая деления сводится к разбиению данного множества на равночисленные подмножества.
Но учителю необходимо знать эти термины, чтобы учитывать оба случая при подборе практических заданий и ситуаций, нацеленных на формирование представлений о смысле деления.

Слайд 36 При изучении зависимости между компонентами деления можно использовать

При изучении зависимости между компонентами деления можно использовать подвижные карточки. Сначала

подвижные карточки. Сначала составляется пример на деление, называются компоненты:

8

: 2 = 4
делимое делитель частное

Слайд 37 Затем учитель предлагает детям составить еще один пример

Затем учитель предлагает детям составить еще один пример на деление и

на деление и на умножение с этими же числами.

Примеры записываются, компоненты называются так же, как в первом примере:
8           :             4            =            2
делимое             частное               делитель

4           ∙            2            =            8
  частное          делитель            делимое

Слайд 38 Под руководством учителя дети делают вывод:
если делимое

Под руководством учителя дети делают вывод: если делимое разделить на частное,

разделить на частное, получится делитель. Если частное умножить на

делитель, получится делимое.

Слайд 39 Частные случаи деления с 1 и 0 основываются

Частные случаи деления с 1 и 0 основываются на взаимосвязи деления

на взаимосвязи деления и умножения:
3:1= 5:1= 18:1= 25:1=
1 ∙

3 = 3 1∙ 5 = 5 1∙18 = 18
1 ∙ 25 = 25

Слайд 40 Рассуждение: разделить 3 на 1 – значит, найти

Рассуждение: разделить 3 на 1 – значит, найти такое число, при

такое число, при умножении на которое 1 получится 3.

Это число 3. Значит, 3:1=3.
После рассмотрения нескольких частных случаев делается вывод:
при делении любого числа на единицу в частном получается то число, которое делили.