Презентация на тему Нормальное распределение: свойства и следствия из них

Содержание

2. Нормальное распределениеЦентральная предельная теорема в применении к
3. Закон нормального распределенияГде:β — среднеквадратичное отклонение (σ);α
4. Свойства нормального распределенияПравило 3 сигм (99,72% значений
5. Проверка распределения на «нормальность»Графический способ (QQ-plot);Статистический критерий Колмогорова-Смирнова (N>50 человек) ;W-критерий Шапиро-Уилка (8
6. Графический способОпределить эмпирические процентили (5%, 10% ...);Посчитать
7. Критерий асимметрии и эксцесса1. Определить среднее арифметическое
8. Правило 3 сигмПри нормальном распределении:M(+/-)σ=68,26%M(+/-)2σ=95,44%M(+/-)3σ=99,72%,M(+/-)3σ - интервал всех возможных значений
9. Стандартная шкалаСтандартизация: перевод измерений в z-шкалу, т.е.
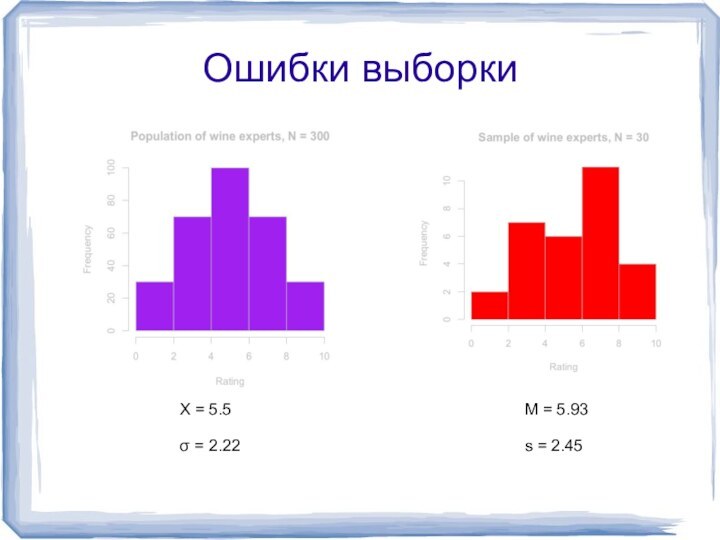
10. Ошибки выборкиM = 5.93 s = 2.45 X = 5.5 σ = 2.22
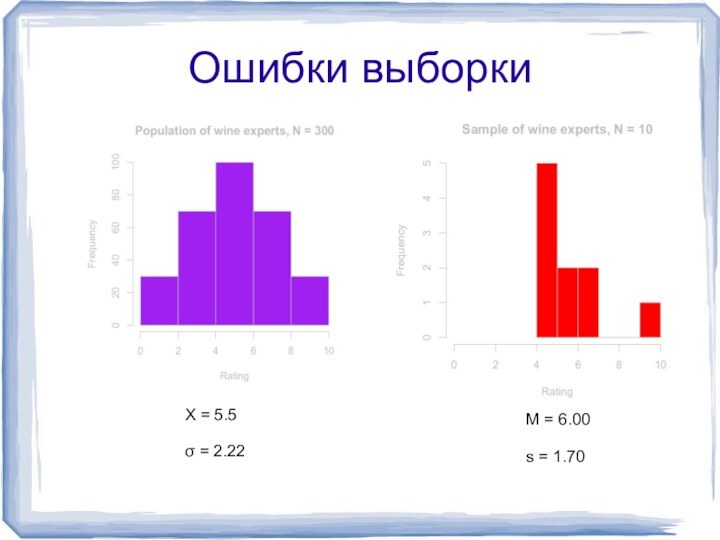
11. Ошибки выборкиX = 5.5 σ = 2.22 M = 6.00 s = 1.70
12. Скачать презентацию
13. Похожие презентации

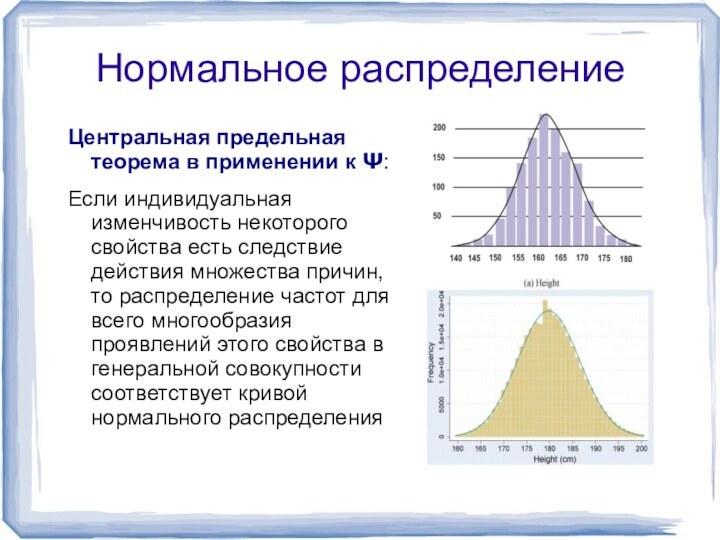
Нормальное распределениеЦентральная предельная теорема в применении к Ψ: Если индивидуальная изменчивость некоторого свойства есть следствие действия множества причин, то распределение частот для всего многообразия проявлений этого свойства в генеральной совокупности соответствует кривой нормального распределения

Главная
Математика
Нормальное распределение: свойства и следствия из них

Нормальное распределение: свойства и следствия из них

Нормальное распределениеЦентральная предельная теорема в применении к Ψ: Если индивидуальная изменчивость некоторого

Закон нормального распределенияГде:β — среднеквадратичное отклонение (σ);α — среднее (М);e, π -

Свойства нормального распределенияПравило 3 сигм (99,72% значений лежат в рамках M+/-3σ)Распределение симметрично

Проверка распределения на «нормальность»Графический способ (QQ-plot);Статистический критерий Колмогорова-Смирнова (N>50 человек) ;W-критерий Шапиро-Уилка (8

Графический способОпределить эмпирические процентили (5%, 10% ...);Посчитать теоретические процентили (через z-значения и

Критерий асимметрии и эксцесса1. Определить среднее арифметическое (М) и стандартное отклонение (σ).2.

Правило 3 сигмПри нормальном распределении:M(+/-)σ=68,26%M(+/-)2σ=95,44%M(+/-)3σ=99,72%,M(+/-)3σ - интервал всех возможных значений

Стандартная шкалаСтандартизация: перевод измерений в z-шкалу, т.е. шкалу со средним М=0 и

Ошибки выборкиM = 5.93 s = 2.45 X = 5.5 σ = 2.22

Ошибки выборкиX = 5.5 σ = 2.22 M = 6.00 s = 1.70

Чтобы не ошибитьсяТочечная оценка параметра=оценка одним числомИнтервальная оценка параметра:Xmin< X

Слайды презентации

Слайд 2 Нормальное распределение
Центральная предельная теорема в применении к Ψ:

Нормальное распределениеЦентральная предельная теорема в применении к Ψ: Если индивидуальная изменчивость

Если индивидуальная изменчивость некоторого свойства есть следствие действия множества

причин, то распределение частот для всего многообразия проявлений этого свойства в генеральной совокупности соответствует кривой нормального распределения

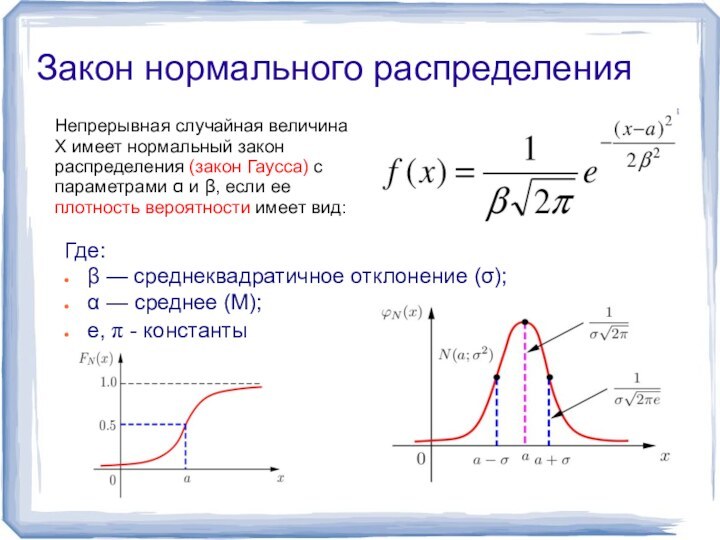
Слайд 3 Закон нормального распределения

Где:
β — среднеквадратичное отклонение (σ);
α —

среднее (М);
e, π - константы
Непрерывная случайная величина X имеет

нормальный закон распределения (закон Гаусса) с параметрами α и β, если ее плотность вероятности имеет вид:

Слайд 4 Свойства нормального распределения
Правило 3 сигм (99,72% значений лежат

Свойства нормального распределенияПравило 3 сигм (99,72% значений лежат в рамках M+/-3σ)Распределение

в рамках M+/-3σ)
Распределение симметрично (А=0), эксцесс (мера остроты пика)

Е = 0
Мода, медиана и среднее совпадают
Значения, лежащие на равном расстоянии от M (среднего), имеют равную частоту в выборке

Слайд 5 Проверка распределения на «нормальность»
Графический способ (QQ-plot);
Статистический критерий Колмогорова-Смирнова

(N>50 человек) ;
W-критерий Шапиро-Уилка (8

ГОСТ Р ИСО 5479—2002

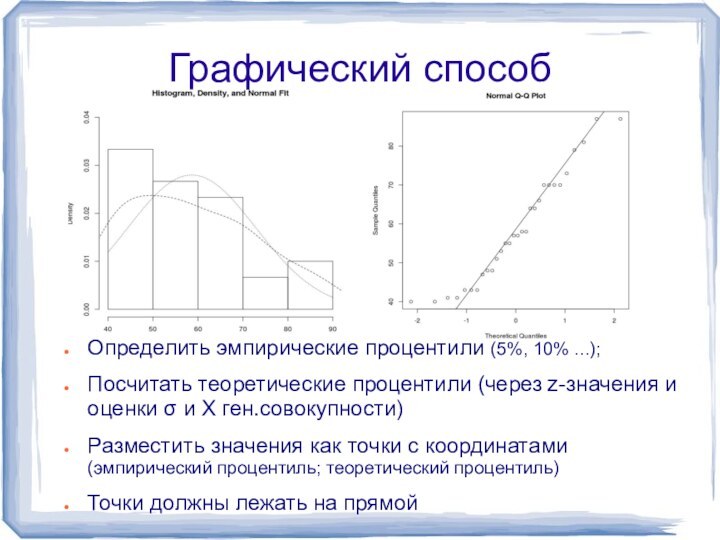
Слайд 6 Графический способ
Определить эмпирические процентили (5%, 10% ...);
Посчитать теоретические

Графический способОпределить эмпирические процентили (5%, 10% ...);Посчитать теоретические процентили (через z-значения

процентили (через z-значения и оценки σ и Х ген.совокупности)
Разместить

значения как точки с координатами (эмпирический процентиль; теоретический процентиль)
Точки должны лежать на прямой

Слайд 7 Критерий асимметрии и эксцесса
1. Определить среднее арифметическое (М)

Критерий асимметрии и эксцесса1. Определить среднее арифметическое (М) и стандартное отклонение

и стандартное отклонение (σ).
2. Рассчитать показатели асимметрии и эксцесса.
А=

Е= -3

3. Рассчитать критические значения А и Е
А Е

4. Если А

Слайд 8 Правило 3 сигм
При нормальном распределении:
M(+/-)σ=68,26%
M(+/-)2σ=95,44%
M(+/-)3σ=99,72%,
M(+/-)3σ - интервал всех

возможных значений

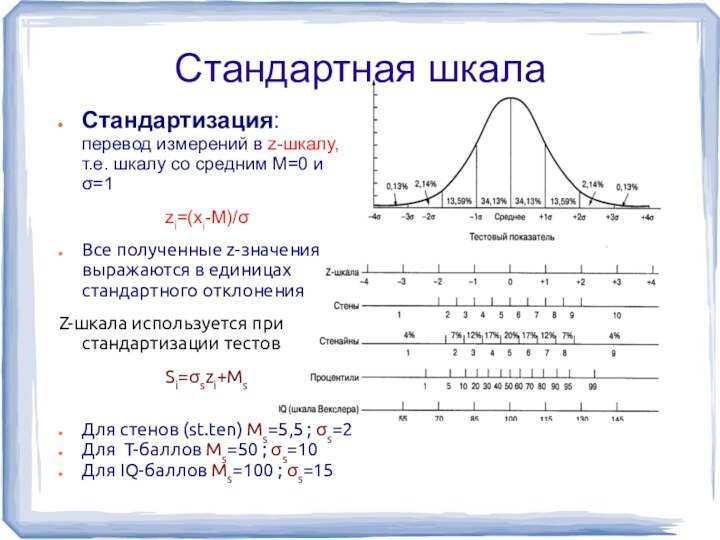
Слайд 9 Стандартная шкала
Стандартизация: перевод измерений в z-шкалу, т.е. шкалу

Стандартная шкалаСтандартизация: перевод измерений в z-шкалу, т.е. шкалу со средним М=0

со средним М=0 и σ=1
zi=(xi-M)/σ
Все полученные z-значения выражаются в

единицах стандартного отклонения
Z-шкала используется при стандартизации тестов
Si=σszi+Ms

Для стенов (st.ten) Ms=5,5 ; σs=2
Для T-баллов Ms=50 ; σs=10
Для IQ-баллов Ms=100 ; σs=15