- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Обработка и анализ числовой информации. Корреляционный анализ
Содержание
- 2. Корреляционный анализ – это метод математической статистики, который позволяет определить степень взаимосвязи между различными параметрами
- 3. РАЗНОВИДНОСТИ КОРРЕЛЯЦИОННОГО АНАЛИЗАПАРНЫЙОценивается степень взаимосвязи отклика Y
- 4. ХАРАКТЕРИСТИКА СТЕПЕНИ ВЗАИМОСВЯЗИ ПАРАМЕТРОВХарактеристикой степени взаимосвязи параметров является статистическая величина, называемая коэффициентом корреляции
- 5. КОЭФФИЦИЕНТ ПАРНОЙ КОРРЕЛЯЦИИKXY- корреляционный момент. Он
- 6. ВЫБОРОЧНАЯ ОЦЕНКА КОЭФФИЦИЕНТА ПАРНОЙ КОРРЕЛЯЦИИсредние выборочные
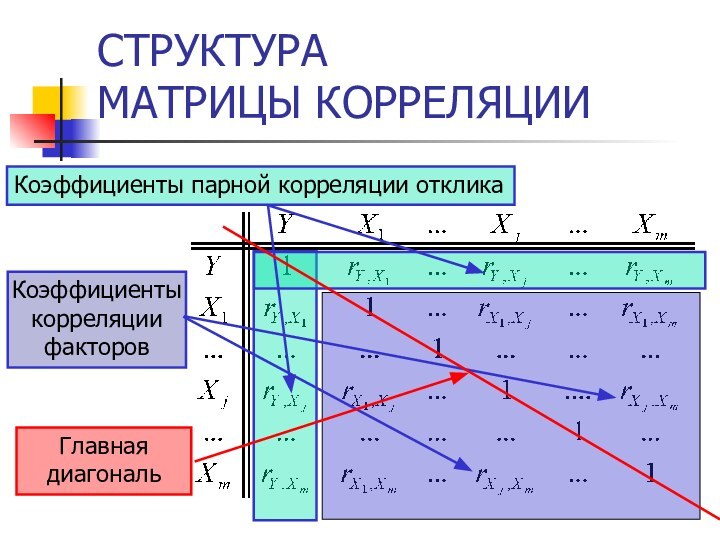
- 7. МАТРИЦА КОРРЕЛЯЦИИТаблица коэффициентов парной корреляции, которые отображают
- 8. СТРУКТУРА МАТРИЦЫ КОРРЕЛЯЦИИКоэффициенты парной корреляции откликаКоэффициенты корреляции факторовГлавная диагональ
- 9. СИММЕТРИЧНОСТЬ МАТРИЦЫ КОРРЕЛЯЦИИМатрица корреляции симметрична относительно главной диагонали
- 10. КОЭФФИЦИЕНТ МНОЖЕСТВЕННОЙ КОРРЕЛЯЦИИ
- 11. СВОЙСТВА КОЭФФИЦИЕНТА КОРРЕЛЯЦИИКоэффициент корреляции не имеет
- 12. СТАТИСТИЧЕСКАЯ ЗНАЧИМОСТЬ КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ Коэффициент корреляции действительно
- 13. УСЛОВИЯ ЗНАЧИМОСТИ КОЭФФИЦИЕНТА ПАРНОЙ КОРРЕЛЯЦИИt –
- 14. УСЛОВИЕ ЗНАЧИМОСТИ КОЭФФИЦИЕНТА МНОЖЕСТВЕННОЙ КОРРЕЛЯЦИИm – число
- 15. ПРИМЕР КОРРЕЛЯЦИОННОГО АНАЛИЗА В MS EXCEL
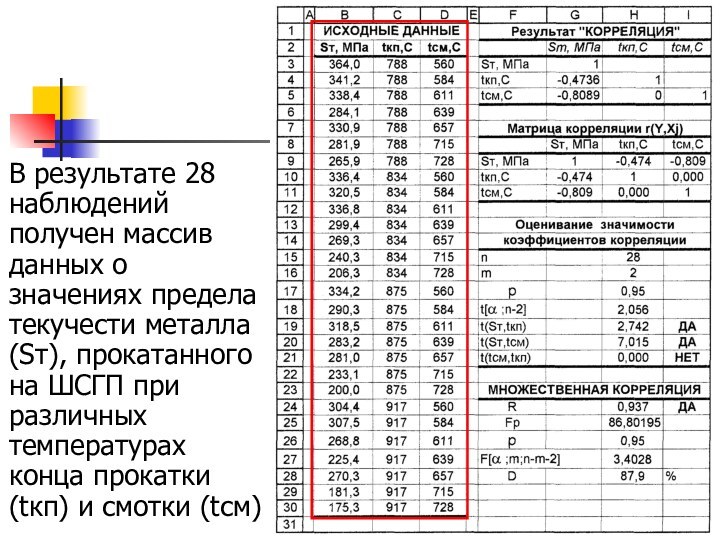
- 16. В результате 28 наблюдений получен массив данных
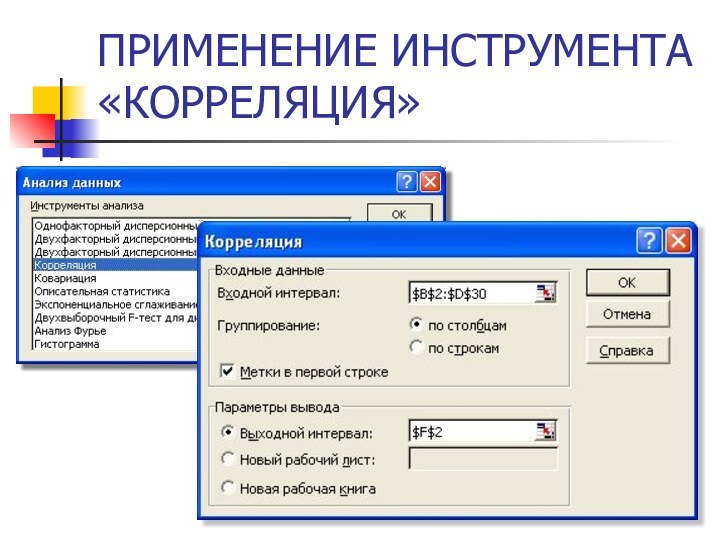
- 17. ПРИМЕНЕНИЕ ИНСТРУМЕНТА «КОРРЕЛЯЦИЯ»
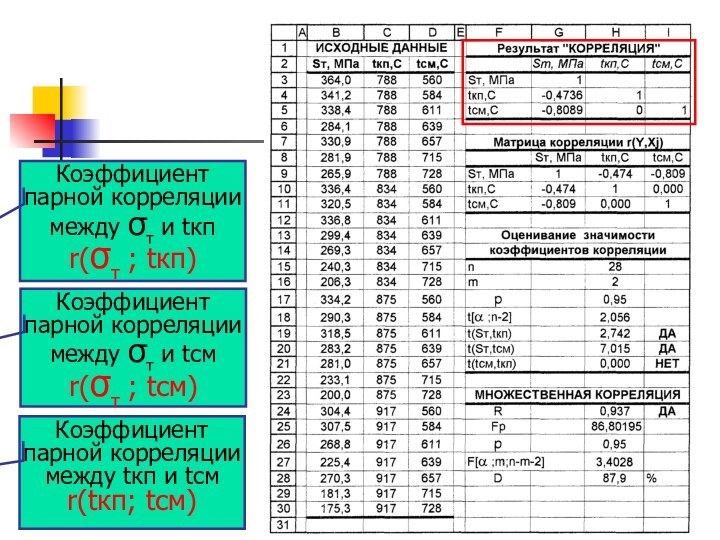
- 18. Коэффициент парной корреляции между σт и
- 19. ПРИМЕНЕНИЕ СТАТИСТИЧЕСКИХ ФУНКЦИЙr(σт ; tкп) =КОРРЕЛ(B3:B30;C3:C30)r(σт ;
- 20. ОЦЕНИВАНИЕ КОЭФФИЦИЕНТОВ ПАРНОЙ КОРРЕЛЯЦИИ=СЧЁТ(B3:B30)=СЧЁТЗ(C2:D2)C клавиатуры=СТЬЮДРАСПОБР(1-H17;H15-2)=ABS(G10)*КОРЕНЬ($H$15-2)/КОРЕНЬ(1-G10^2)=ABS(G11)*КОРЕНЬ($H$15-2)/КОРЕНЬ(1-G11^2)=ABS(H11)*КОРЕНЬ($H$15-2)/КОРЕНЬ(1-H11^2)=ЕСЛИ(H19>$H$18;"ДА";"НЕТ")
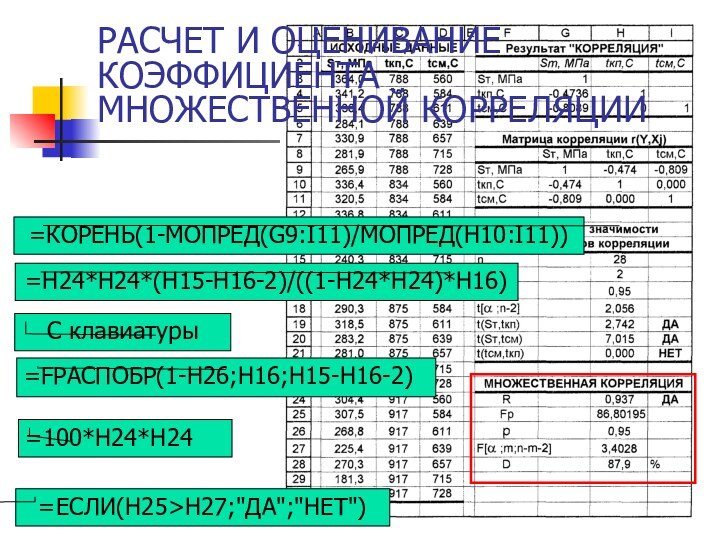
- 21. РАСЧЕТ И ОЦЕНИВАНИЕ КОЭФФИЦИЕНТА МНОЖЕСТВЕННОЙ КОРРЕЛЯЦИИ=КОРЕНЬ(1-МОПРЕД(G9:I11)/МОПРЕД(H10:I11))=H24*H24*(H15-H16-2)/((1-H24*H24)*H16)C клавиатуры=FРАСПОБР(1-H26;H16;H15-H16-2)=ЕСЛИ(H25>H27;"ДА";"НЕТ")=100*H24*H24
- 22. Связь между какими величинами анализировалась?Анализировалась связь между
- 23. Какие коэффициенты парной корреляции являются статистически
- 24. О чем это свидетельствует?Следовательно, предел текучести металла,
- 25. Является ли значимым коэффициент множественной корреляции? Что
- 26. Скачать презентацию
- 27. Похожие презентации
Корреляционный анализ – это метод математической статистики, который позволяет определить степень взаимосвязи между различными параметрами











![Обработка и анализ числовой информации. Корреляционный анализ УСЛОВИЯ ЗНАЧИМОСТИ КОЭФФИЦИЕНТА ПАРНОЙ КОРРЕЛЯЦИИt – рассчитанное число Стьюдентаt[α;n-2] – табличное](/img/tmb/15/1430065/995a81001e1f972c7131401c4cf8fc6b-720x.jpg)
![Обработка и анализ числовой информации. Корреляционный анализ УСЛОВИЕ ЗНАЧИМОСТИ КОЭФФИЦИЕНТА МНОЖЕСТВЕННОЙ КОРРЕЛЯЦИИm – число факторов;Fp – рассчитанное число Фишера;F[α;m;n-m-2]](/img/tmb/15/1430065/98e465dc9597e293a9bced29bca9229e-720x.jpg)








Слайд 2
Корреляционный анализ – это метод математической статистики, который
позволяет определить степень взаимосвязи между различными параметрами
Слайд 3
РАЗНОВИДНОСТИ КОРРЕЛЯЦИОННОГО АНАЛИЗА
ПАРНЫЙ
Оценивается степень взаимосвязи отклика Y и
одного фактора X
МНОЖЕСТВЕННЫЙ
Оценивается степень взаимосвязи отклика Y и нескольких
факторов
X1, … , Xj, … Xm
Слайд 4
ХАРАКТЕРИСТИКА СТЕПЕНИ ВЗАИМОСВЯЗИ ПАРАМЕТРОВ
Характеристикой степени взаимосвязи параметров является
статистическая величина, называемая коэффициентом корреляции
Слайд 5
КОЭФФИЦИЕНТ
ПАРНОЙ КОРРЕЛЯЦИИ
KXY- корреляционный момент. Он представляет собой
математическое ожидание произведения отклонений значений x и y случайных
величин X и Y от их математических ожиданий M(X) и M(Y);D(X)- дисперсия случайной величины X;
D(Y)- дисперсия случайной величины Y.
Слайд 6
ВЫБОРОЧНАЯ ОЦЕНКА КОЭФФИЦИЕНТА
ПАРНОЙ КОРРЕЛЯЦИИ
средние выборочные значения фактора
и отклика;
выборочные стандартные отклонения фактора и отклика;
число наблюдений.
Слайд 7
МАТРИЦА КОРРЕЛЯЦИИ
Таблица коэффициентов парной корреляции, которые отображают взаимодействия
отклика с каждым из факторов а также факторов между
собой
Слайд 8
СТРУКТУРА
МАТРИЦЫ КОРРЕЛЯЦИИ
Коэффициенты парной корреляции отклика
Коэффициенты корреляции факторов
Главная
диагональ
Слайд 9
СИММЕТРИЧНОСТЬ МАТРИЦЫ КОРРЕЛЯЦИИ
Матрица корреляции симметрична относительно главной диагонали
Слайд 11
СВОЙСТВА
КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ
Коэффициент корреляции не имеет размерности и
поэтому сопоставим для различных статистических рядов.
Значение коэффициента корреляции
лежит в пределах от -1 до +1. Если коэффициент корреляции равен 1, между параметрами существует функциональная зависимость.
Коэффициент корреляции должен быть проверен на значимость.
Слайд 12
СТАТИСТИЧЕСКАЯ ЗНАЧИМОСТЬ КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ
Коэффициент корреляции действительно
не
равен нулю?
Коэффициент корреляции вычисляется
на основании выборочных данных
и поэтому является случайной величиной
Слайд 13
УСЛОВИЯ ЗНАЧИМОСТИ КОЭФФИЦИЕНТА
ПАРНОЙ КОРРЕЛЯЦИИ
t – рассчитанное число
Стьюдента
t[α;n-2] – табличное число Стьюдента
rmin – минимальное статистически значимое
значение коэффициента корреляции при доверительной вероятности p=1-α
Слайд 14
УСЛОВИЕ ЗНАЧИМОСТИ КОЭФФИЦИЕНТА МНОЖЕСТВЕННОЙ КОРРЕЛЯЦИИ
m – число факторов;
Fp
– рассчитанное число Фишера;
F[α;m;n-m-2] – табличное число Фишера при
доверительной вероятности p=1-α.Слайд 16 В результате 28 наблюдений получен массив данных о
значениях предела текучести металла (Sт), прокатанного на ШСГП при
различных температурах конца прокатки (tкп) и смотки (tсм)
Слайд 18
Коэффициент парной корреляции
между σт и tкп
r(σт ;
tкп)
Коэффициент парной корреляции
между σт и tсм
r(σт ; tсм)
Коэффициент
парной корреляции
между tкп и tсм
r(tкп; tсм)
Слайд 19
ПРИМЕНЕНИЕ СТАТИСТИЧЕСКИХ ФУНКЦИЙ
r(σт ; tкп) =КОРРЕЛ(B3:B30;C3:C30)
r(σт ; tсм)
=КОРРЕЛ(B3:B30;D3:D30)
r(tкп ; tсм) =КОРРЕЛ(C3:C30;D3:D30)
r(tкп; σт) =КОРРЕЛ(C3:C30;B3:B30)
r(tсм; σт) =КОРРЕЛ(D3:D30;B3:B30)
r(tсм;tкп) =КОРРЕЛ(D3:D30;С3:С30)
Матрица
корреляции действительно симметрична относительно главной диагонали
Слайд 20
ОЦЕНИВАНИЕ КОЭФФИЦИЕНТОВ
ПАРНОЙ КОРРЕЛЯЦИИ
=СЧЁТ(B3:B30)
=СЧЁТЗ(C2:D2)
C клавиатуры
=СТЬЮДРАСПОБР(1-H17;H15-2)
=ABS(G10)*КОРЕНЬ($H$15-2)/КОРЕНЬ(1-G10^2)
=ABS(G11)*КОРЕНЬ($H$15-2)/КОРЕНЬ(1-G11^2)
=ABS(H11)*КОРЕНЬ($H$15-2)/КОРЕНЬ(1-H11^2)
=ЕСЛИ(H19>$H$18;"ДА";"НЕТ")
Слайд 21
РАСЧЕТ И ОЦЕНИВАНИЕ КОЭФФИЦИЕНТА МНОЖЕСТВЕННОЙ КОРРЕЛЯЦИИ
=КОРЕНЬ(1-МОПРЕД(G9:I11)/МОПРЕД(H10:I11))
=H24*H24*(H15-H16-2)/((1-H24*H24)*H16)
C клавиатуры
=FРАСПОБР(1-H26;H16;H15-H16-2)
=ЕСЛИ(H25>H27;"ДА";"НЕТ")
=100*H24*H24
Слайд 22
Связь между какими величинами анализировалась?
Анализировалась связь между пределом
текучести металла σт, температурой конца прокатки tкп и смотки
tсм при прокатке на ШСГП.
Слайд 23
Какие коэффициенты
парной корреляции являются статистически значимыми?
С
доверительной вероятностью 95% статистически значимыми являются коэффициенты корреляции между
пределом текучести и температурой конца прокатки r(σт ; tкп)=-0,474 а также между пределом текучести и температурой смотки r(σт ; tсм)=-0,809.Значимость коэффициентов подтверждается тем, что соответствующие расчетные числа Стьюдента t(σт ; tкп)=2,742 и t(σт ; tсм)=7,015 больше табличного t[0,05;26]=2,056.
Слайд 24
О чем это свидетельствует?
Следовательно, предел текучести металла, прокатанного
на ШСГП, связан с температурой конца прокатки и смотки.
Так как коэффициенты корреляции отрицательные, увеличение как температуры прокатки, так и температуры смотки уменьшает предел текучести прокатанного металла.
Так как |r(σт ; tсм)|>| r(σт ; tкп) |, степень влияния температуры смотки больше чем температуры конца прокатки.
Слайд 25 Является ли значимым коэффициент множественной корреляции? Что это
означает?
С доверительной вероятностью 95% коэффициент множественной корреляции
R(σт;tкп;tсм)=0,937 является
статистически значимым, т. к. расчетное число Фишера Fp=86,802 больше табличного F[0,05;2;24]=3,4028. Это означает, что предел текучести металла, прокатанного на ШСГП, обусловлен совместным действием температуры конца прокатки и смотки.