Слайд 2
Эпюр прямой
Положение прямой линии однозначно в пространстве определяется
заданием двух ее точек.
Комплексный чертеж прямой может быть представлен
двумя проекциями прямой.
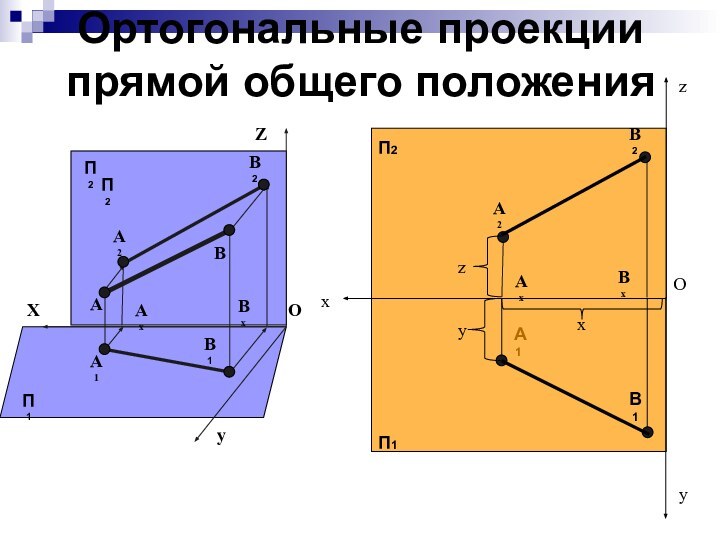
Если прямая не параллельна ни одной плоскости проекций, ее называют прямой общего положения. Такая прямая изображена на рисунке.
Слайд 3
Ортогональные проекции прямой общего положения
X
Z
y
O
A
B
A2
A1
А1
Ax
П2
П1
Bx
B2
B1
П2
П2
П1
A2
Ax
Bx
B2
В1
x
z
y
O
x
z
y
Слайд 4
Следы прямой
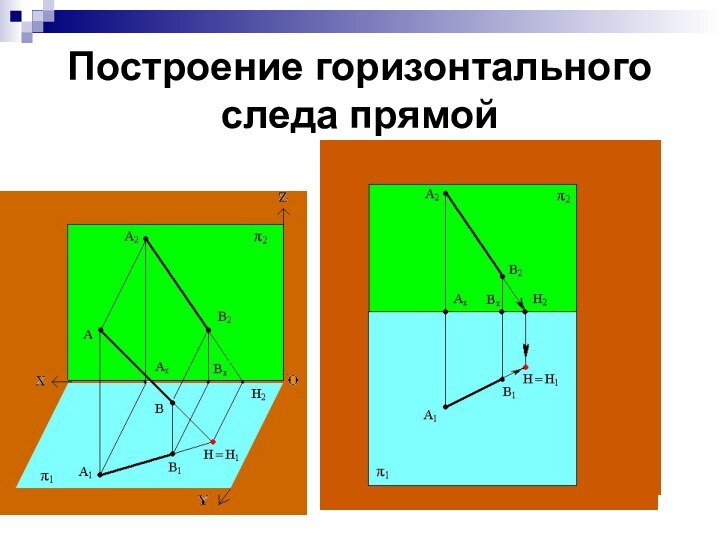
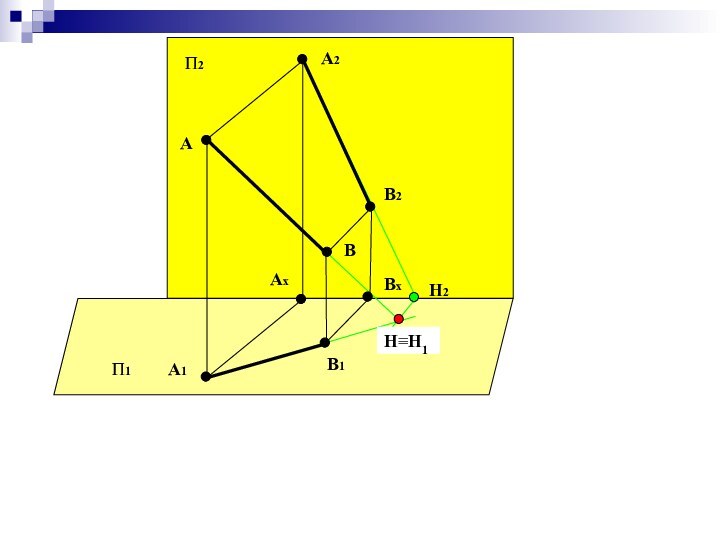
Прямая общего положения пересекает все основные плоскости
проекций. Точку пересечения (встречи) прямой с плоскостью проекций называют
следом прямой.
Слайд 5
Построение горизонтального следа прямой
Слайд 7
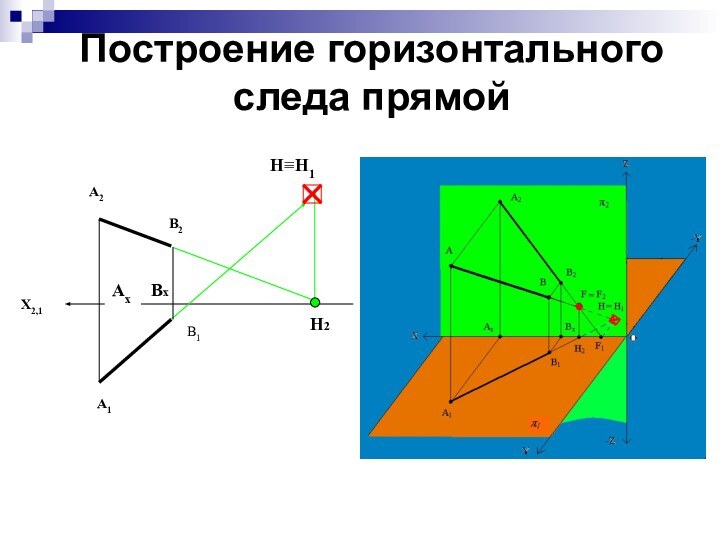
Построение горизонтального следа прямой
В1
Аx
А1
X2,1
А2
В2
H2
Вх
Н≡Н1
Слайд 8
Частные случаи расположения прямой
Кроме общего случая существуют частные
случаи расположения прямой по отношению к заданной системе плоскостей
проекций:
А. Прямая параллельна плоскости проекции.
Б. Прямая перпендикулярна плоскости проекции.
В. Прямая принадлежит плоскости проекции (частный случай параллельности).
Слайд 9
Прямые, параллельные плоскостям проекций (горизонталь, фронталь)
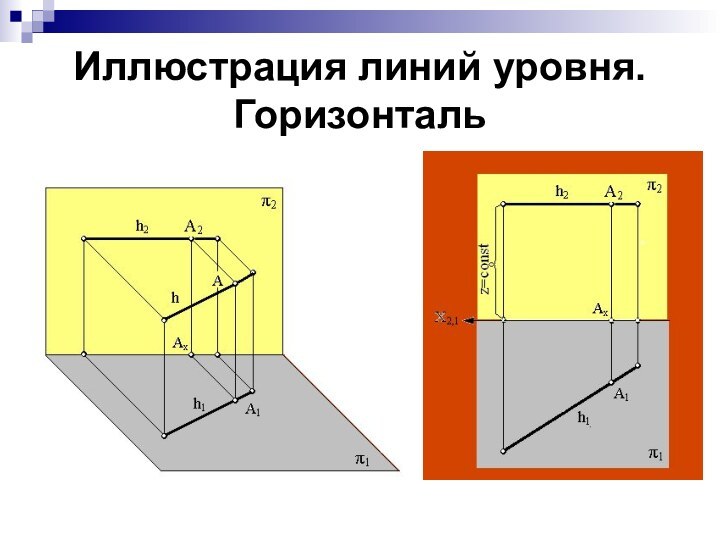
Горизонталь – прямая,
параллельная горизонтальной плоскости проекции: h || π1.
Все
точки горизонтали удалены на одинаковые расстояния от плоскости π1 .
Фронтальная проекция горизонтали h2 || оси x. Горизонтальная проекция может занимать любое положение.
Слайд 10
Иллюстрация линий уровня. Горизонталь
Слайд 11
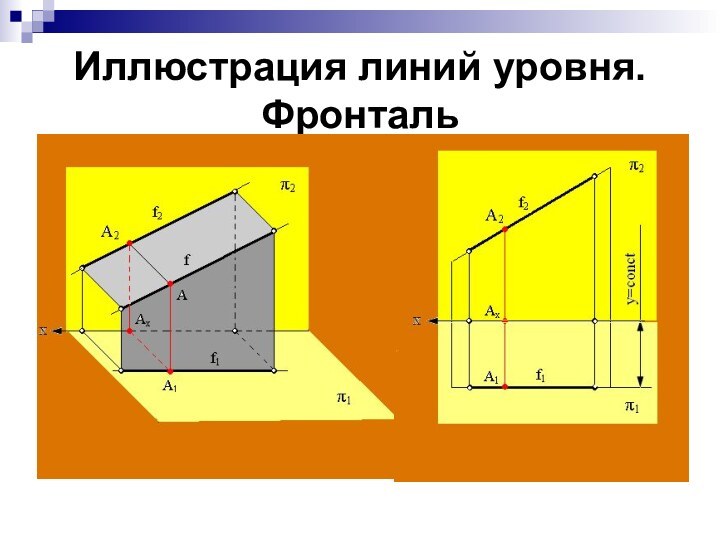
Фронталь – прямая, параллельная фронтальной плоскости проекции: f
|| π2.
Все точки фронтали удалены на одинаковые
расстояния от плоскости π2.
Горизонтальная проекция f1 || оси x. Фронтальная проекция может занимать любое положение.
Слайд 12
Иллюстрация линий уровня. Фронталь
Слайд 13
Проецирующие прямые
Это прямые, перпендикулярные к плоскостям
проекций.
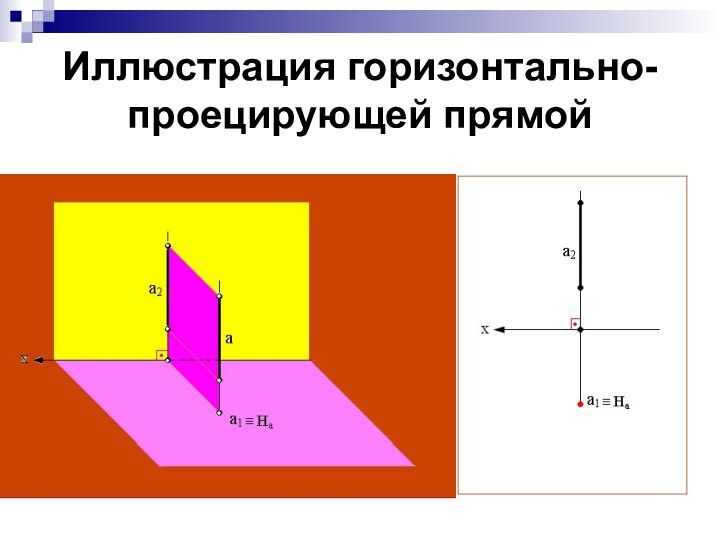
Горизонтально-проецирующая – прямая, перпендикулярная горизонтальной плоскости
проекции.
Такая прямая проецируется на плоскость π1 в точку; ее фронтальная проекция перпендикулярна оси x.
Слайд 14
Иллюстрация горизонтально-проецирующей прямой
Слайд 15
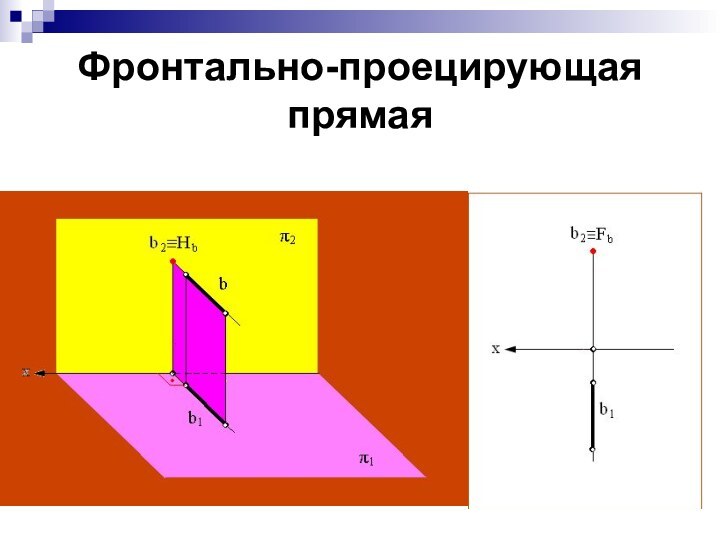
Фронтально-проецирующая – прямая, перпендикулярная фронтальной плоскости
проекции.
Эта прямая проецируется на плоскость π2 в
точку, а ее горизонтальная проекция перпендикулярна оси x.
Слайд 17
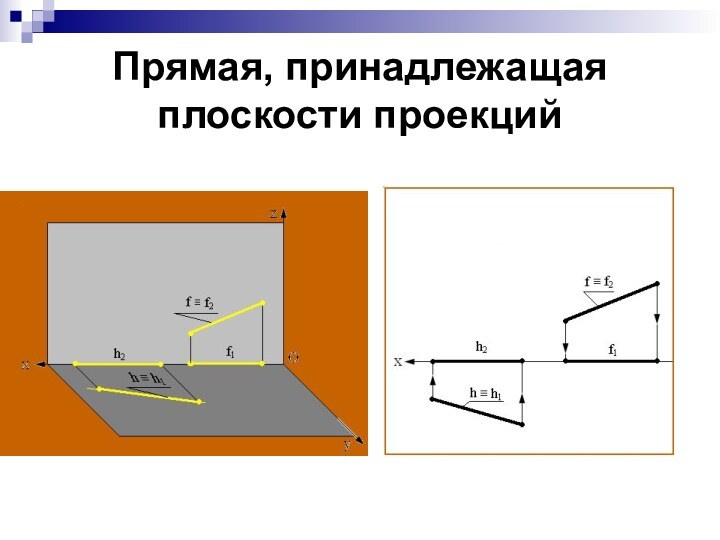
Прямая, принадлежащая плоскости проекций
Слайд 18
Ортогональная проекция плоскости
Плоскость является простейшей поверхностью.
Положение плоскости
в пространстве однозначно определяется тремя различными точками, не принадлежащими
одной прямой.
Слайд 19
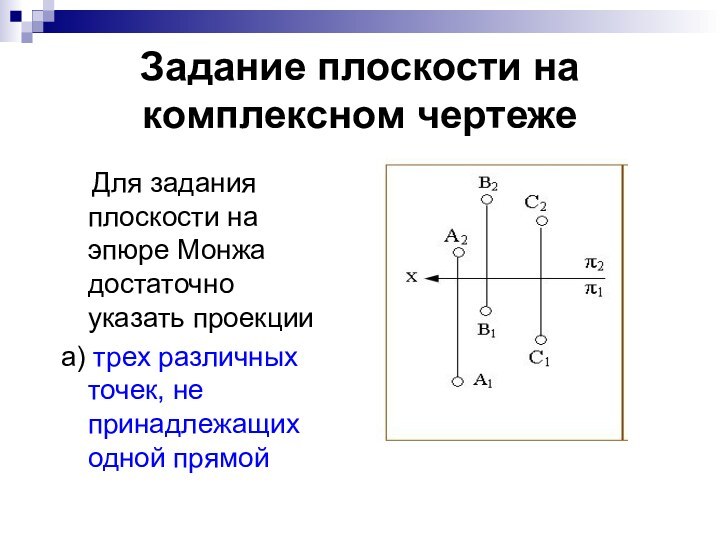
Задание плоскости на комплексном чертеже
Для задания
плоскости на эпюре Монжа достаточно указать проекции
а) трех различных
точек, не принадлежащих одной прямой
Слайд 20
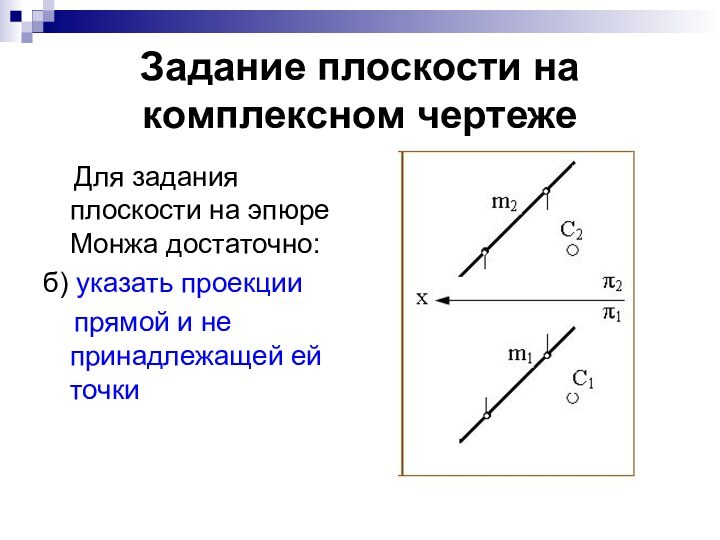
Задание плоскости на комплексном чертеже
Для задания
плоскости на эпюре Монжа достаточно:
б) указать проекции
прямой и не принадлежащей ей точки
Слайд 21
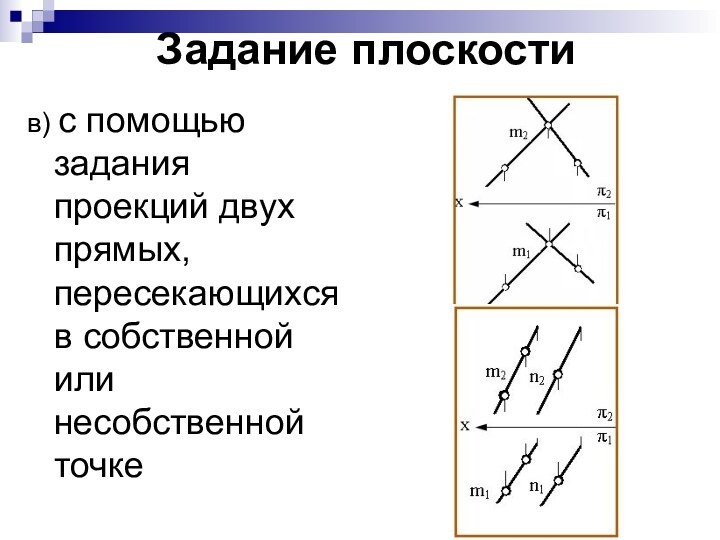
Задание плоскости
в) с помощью задания проекций двух прямых,
пересекающихся в собственной или несобственной точке
Слайд 22
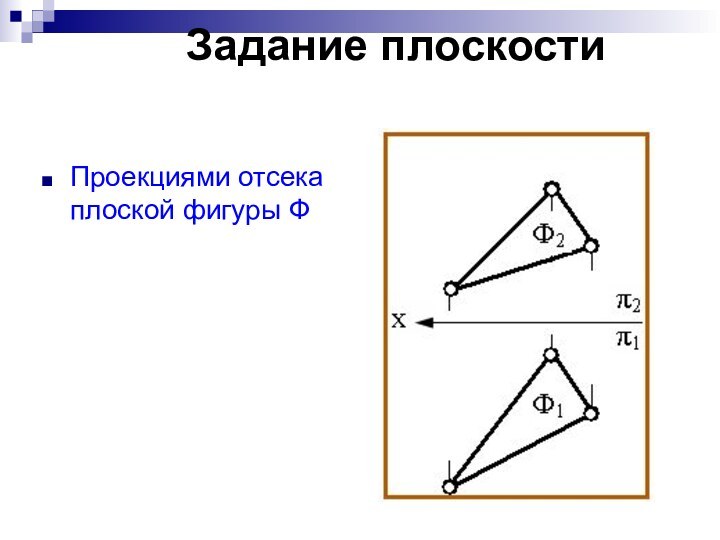
Задание плоскости
Проекциями отсека плоской фигуры Ф
Слайд 23
След плоскости
Линия пересечения плоскости с плоскостями проекций называется
следом плоскости.
Следов всего три
Например: − горизонтальный
след плоскости (поверхности);
− фронтальный след плоскости
(поверхности);
− профильный след плоскости
(поверхности).
h0
f 0
p0
Слайд 24
Задание плоскости следами
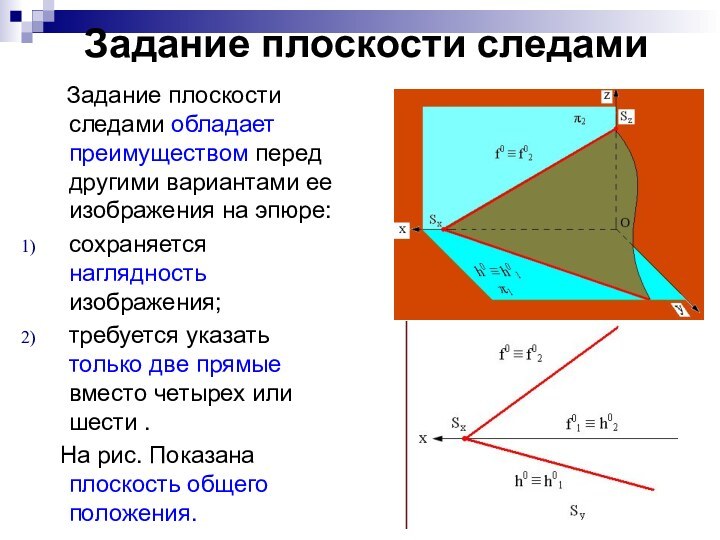
Задание плоскости следами
обладает преимуществом перед другими вариантами ее изображения на эпюре:
сохраняется наглядность изображения;
требуется указать только две прямые вместо четырех или шести .
На рис. Показана плоскость общего положения.
Слайд 25
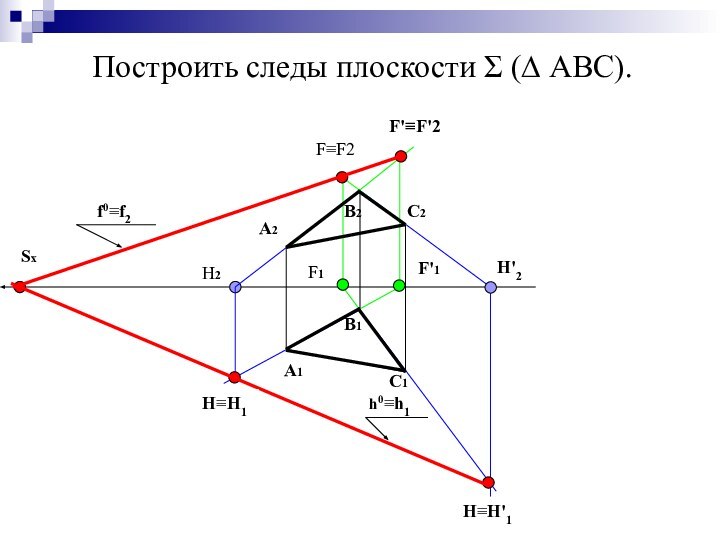
Построить следы плоскости Σ (∆ АВС).
А1
А2
В2
В1
С2
С1
Sx
F1
H2
F≡F2
F'≡F'2
F'1
Н≡Н1
Н≡Н'1
Н'2
h0≡h1
f0≡f2
Слайд 26
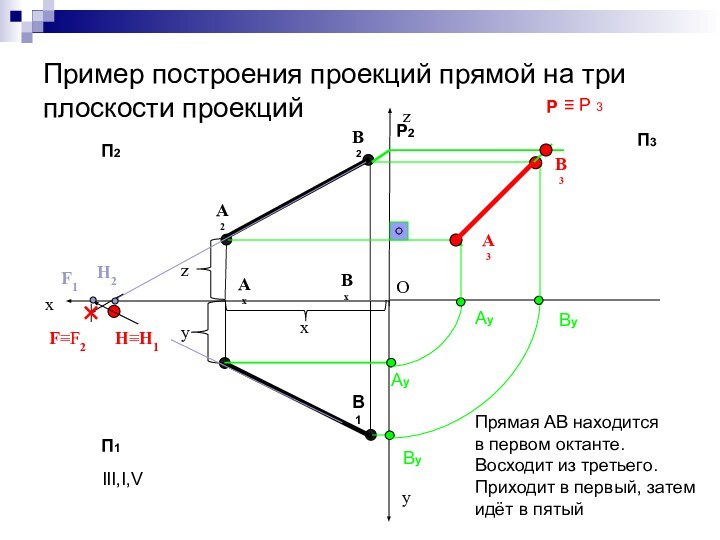
Пример построения проекций прямой на три плоскости проекций
П2
П1
A2
Ax
Bx
B2
В1
x
z
y
O
x
z
y
Ау
Ау
A3
Bу
Bу
П3
B3
Н≡Н1
Н2
F≡F2
F1
Прямая
АВ находится
в первом октанте.
Восходит из третьего.
Приходит в
первый, затем
идёт в пятый
III,I,V
P
≡ P 3
P2
Слайд 27
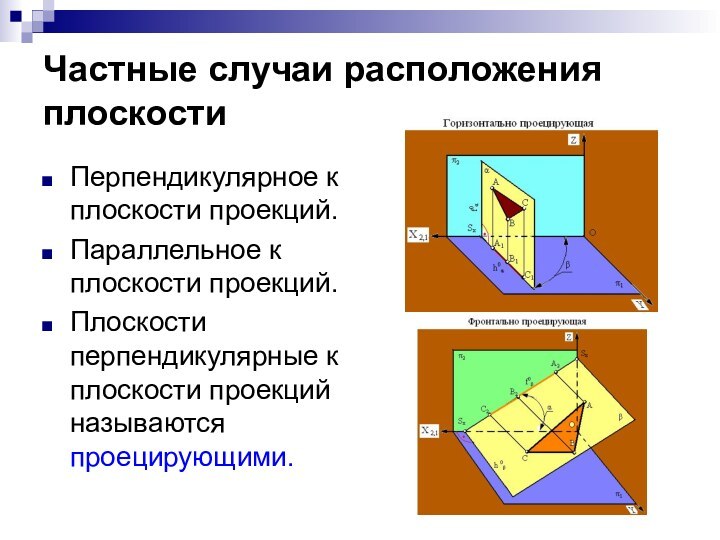
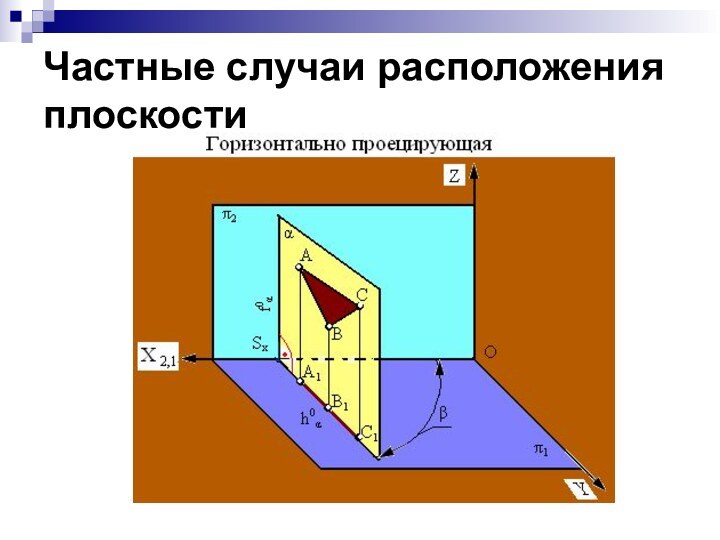
Частные случаи расположения плоскости
Перпендикулярное к плоскости проекций.
Параллельное к
плоскости проекций.
Плоскости перпендикулярные к плоскости проекций называются проецирующими.
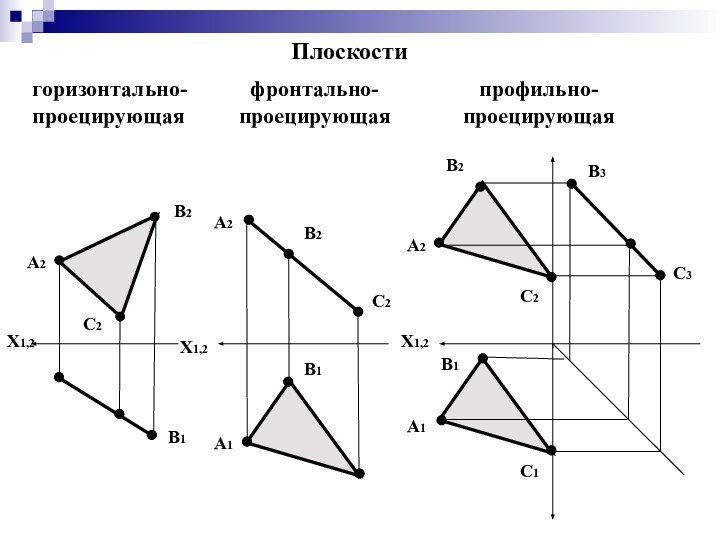
Слайд 28
горизонтально-проецирующая
фронтально-проецирующая
профильно-проецирующая
Плоскости
Х1,2
А1
А2
А1
А2
А2
В3
В2
В2
В2
С2
С3
С2
С2
В1
В1
В1
С1
Х1,2
Х1,2
Слайд 29
Частные случаи расположения плоскости
Слайд 30
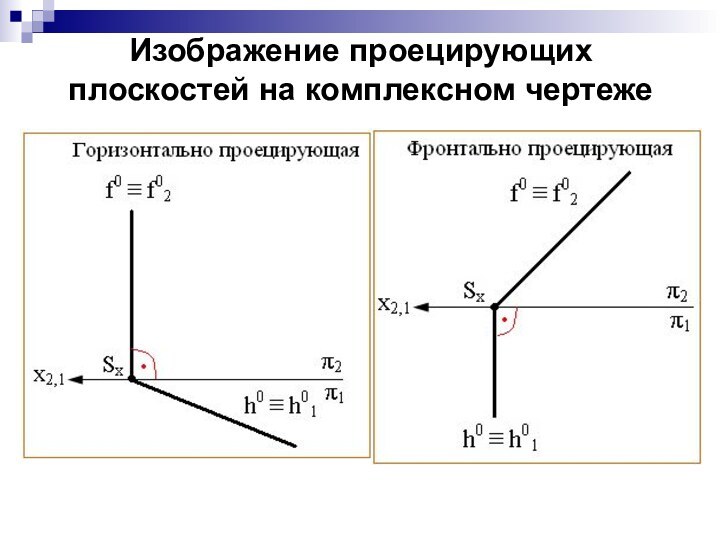
Изображение проецирующих плоскостей на комплексном чертеже
Слайд 31
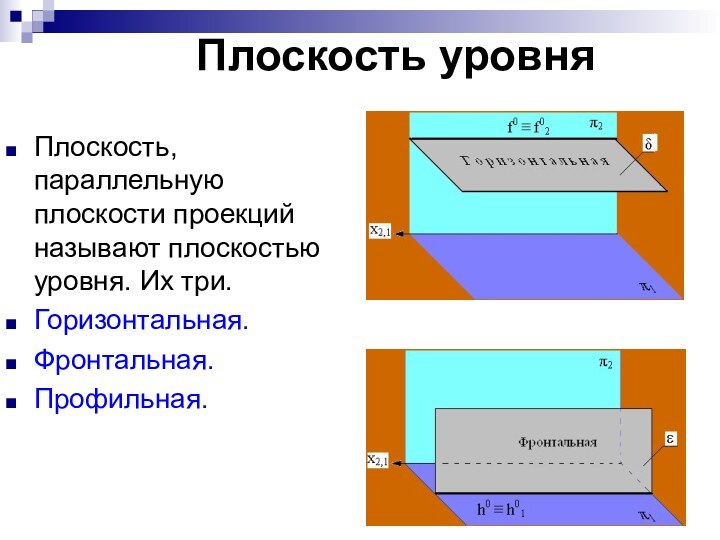
Плоскость уровня
Плоскость, параллельную плоскости проекций называют плоскостью
уровня. Их три.
Горизонтальная.
Фронтальная.
Профильная.
Слайд 32
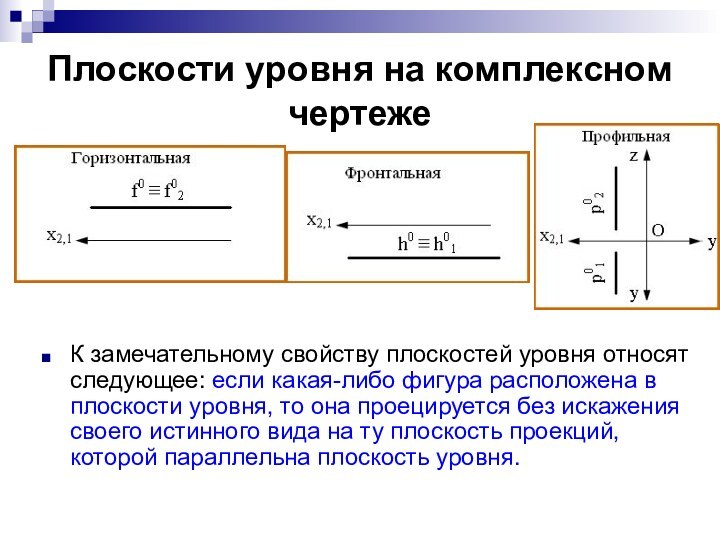
Плоскости уровня на комплексном чертеже
К замечательному свойству плоскостей
уровня относят следующее: если какая-либо фигура расположена в плоскости
уровня, то она проецируется без искажения своего истинного вида на ту плоскость проекций, которой параллельна плоскость уровня.
Слайд 33
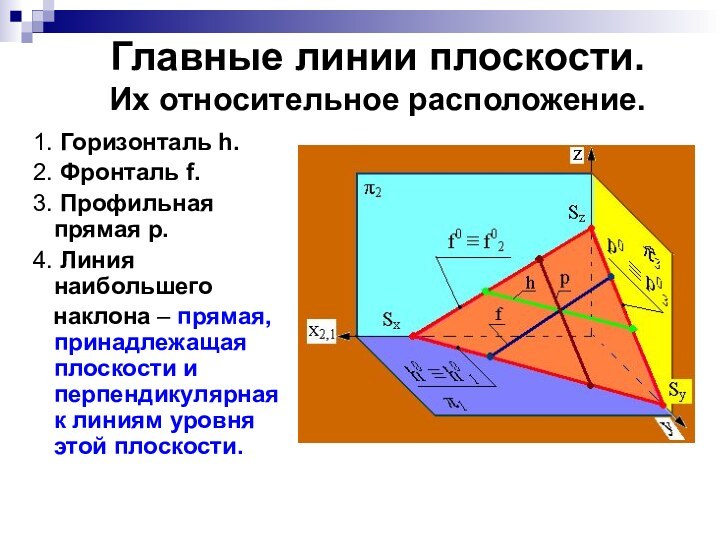
Главные линии плоскости.
Их относительное расположение.
1. Горизонталь
h.
2. Фронталь f.
3. Профильная прямая p.
4. Линия наибольшего
наклона – прямая, принадлежащая плоскости и перпендикулярная к линиям уровня этой плоскости.
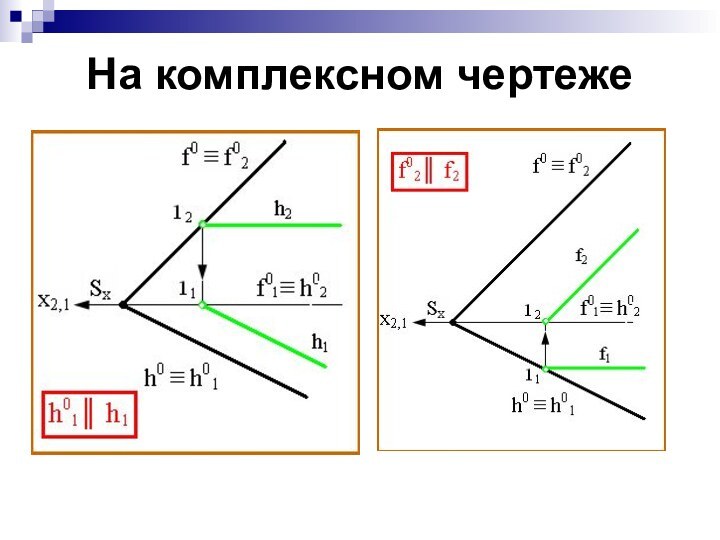
Слайд 35
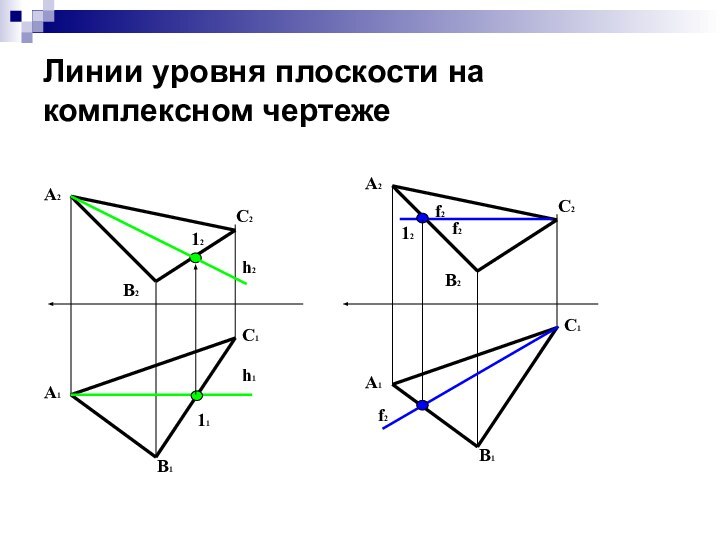
Линии уровня плоскости на комплексном чертеже
А1
В1
С1
А2
В2
С2
h1
11
12
h2
А1
В1
С1
А2
В2
С2
f2
12
f2
f2
Слайд 36
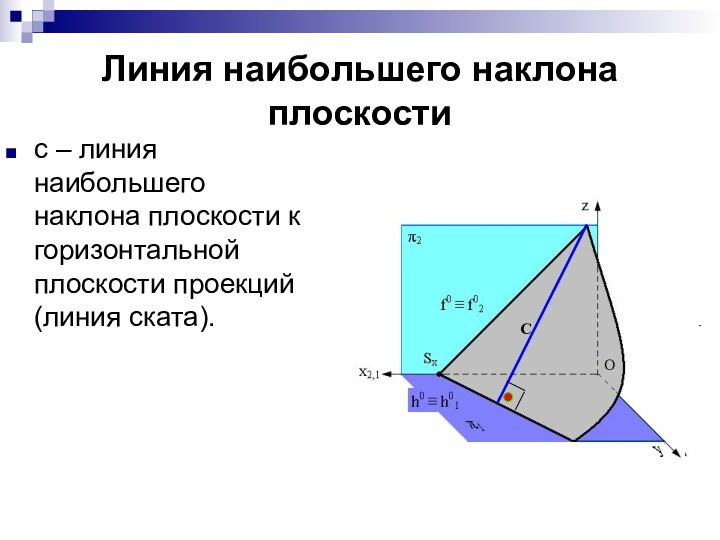
Линия наибольшего наклона плоскости
с – линия наибольшего наклона
плоскости к горизонтальной плоскости проекций (линия ската).
С
Слайд 37
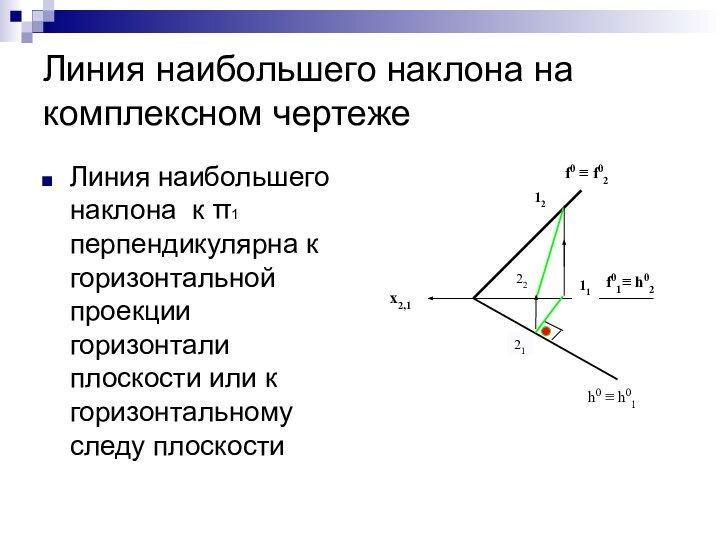
Линия наибольшего наклона на комплексном чертеже
Линия наибольшего наклона
к π1
перпендикулярна к горизонтальной проекции горизонтали плоскости или к горизонтальному следу плоскости
11
12
21
22
x2,1
f0 ≡ f02
h0 ≡ h01
f01≡ h02
Слайд 38
Определение расстояния между двумя точками способом прямоугольного треугольника
Натуральная
величина отрезка равна гипотенузе прямоугольного треугольника, построенного на двух
катетах один из которых проекция отрезка, а второй – разница координат начала и конца отрезка в другой плоскости проекций.
Слайд 39
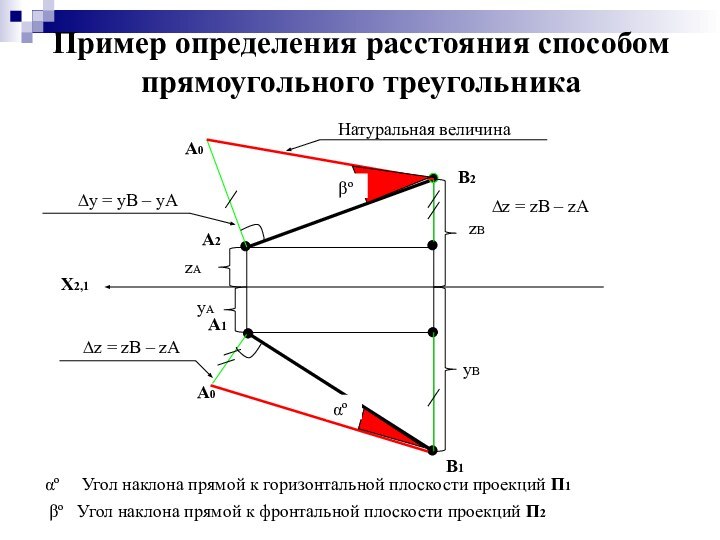
Пример определения расстояния способом прямоугольного треугольника
X2,1
A2
B2
B1
A1
A0
A0
αº
βº
Натуральная величина
yA
yB
∆y =
yB – yA
zB
zA
∆z = zB – zA
αº
Угол
наклона прямой к горизонтальной плоскости проекций П1
βº Угол наклона прямой к фронтальной плоскости проекций П2
∆z = zB – zA
Слайд 40
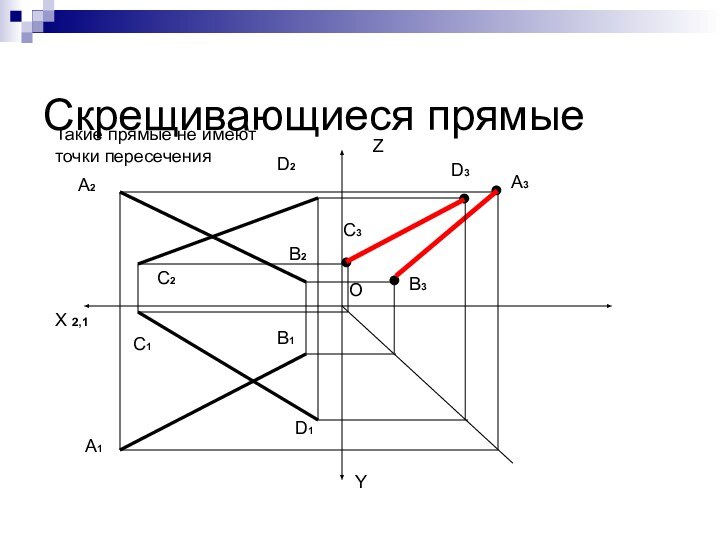
Взаимное положение двух прямых
Прямые в пространстве могут пересекаться
и скрещиваться. Пересечение может быть в несобственной точке. В
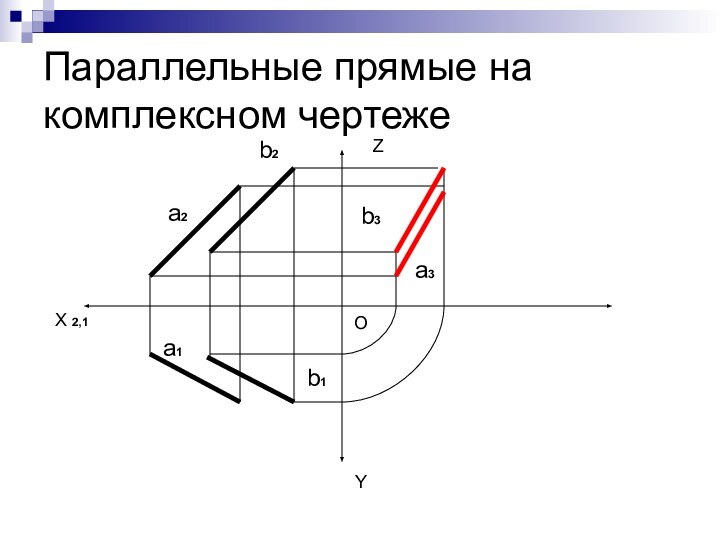
этом случае прямые называют параллельными. Прямые параллельны, если параллельны их проекции. И наоборот.
Слайд 41
Параллельные прямые на комплексном чертеже
а2
а1
b2
b1
X 2,1
Y
Z
O
а3
b3
Слайд 42
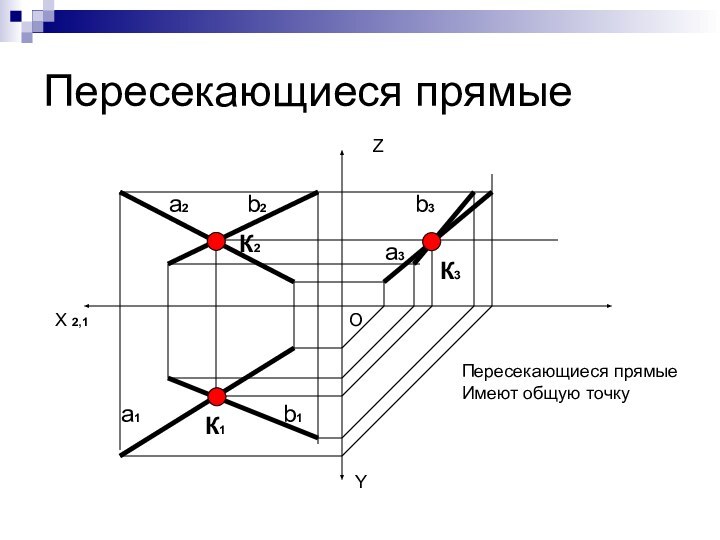
Пересекающиеся прямые
X 2,1
Y
Z
O
Пересекающиеся прямые
Имеют общую точку
а2
а1
b2
b1
а3
b3
К3
К2
К1