- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Определитель. Линейная алгебра
Содержание
- 2. Каждой квадратной матрице А можно поставить в
- 3. Каждой квадратной матрице А можно поставить в
- 4. Вычисление определителей1. n = 12. n = 2
- 5. Вычисление определителей3. n = 3
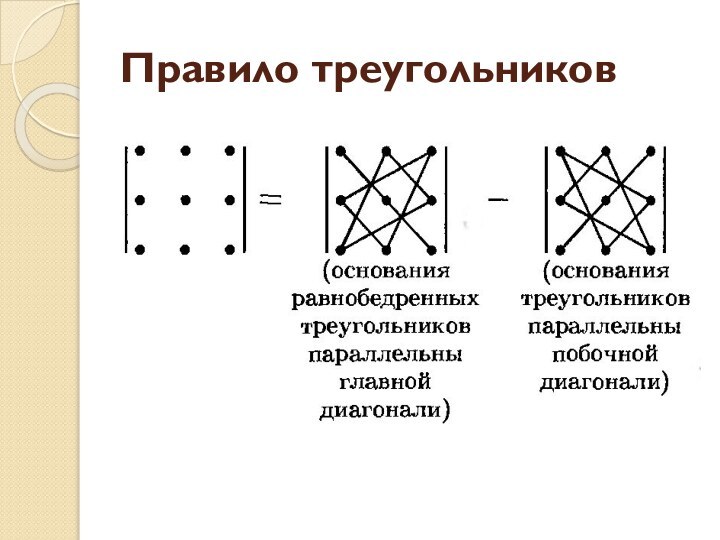
- 6. Правило треугольников
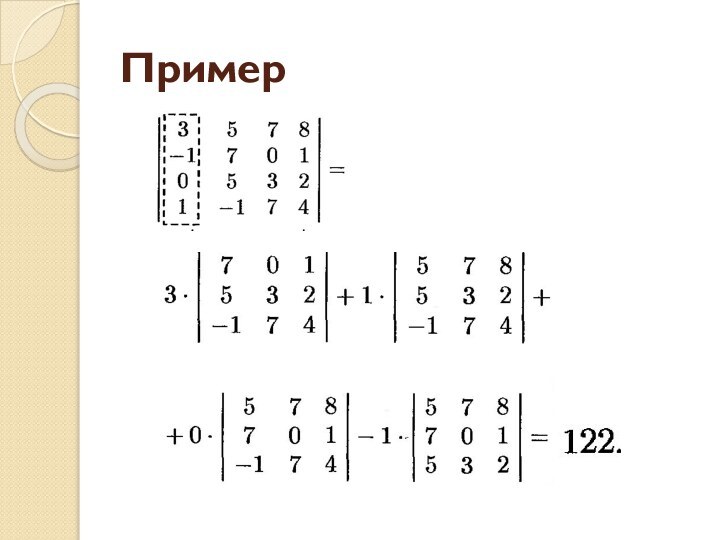
- 7. Пример
- 8. ЗаданияРешить уравнение
- 9. СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ
- 10. 1.Равноправность строк и столбцовОпределитель матрицы не изменится при её транспонировании
- 11. 2. При перестановке двух строк или столбцов определитель меняет знак
- 12. 3.Определитель, имеющий два одинаковых столбца (две одинаковых строки), равен нулю
- 13. 4. Общий множитель элементов строки (столбца) можно вынести за знак определителя
- 14. 5. Если элементы строки (столбца) представляют собой
- 15. 6. Определитель не изменится, если к элементам
- 16. ОпределенияМинором некоторого элемента aij n-го порядка называется
- 17. ОпределенияАлгебраическим дополнением некоторого элемента aij называется его
- 18. 7. Разложение определителя по строке или столбцуОпределитель
- 19. ПримерНайти определитель матрицы
- 20. Пример
- 21. Скачать презентацию
- 22. Похожие презентации
Каждой квадратной матрице А можно поставить в соответствие число, называемое определителем (детерминантом) этой матрицы det A |A|



















Слайд 2 Каждой квадратной матрице А можно поставить в соответствие
число, называемое определителем (детерминантом) этой матрицы
A |A|Слайд 3 Каждой квадратной матрице А можно поставить в соответствие
число, называемое определителем (детерминантом) этой матрицы
det
A |A| ΔСлайд 14 5. Если элементы строки (столбца) представляют собой суммы
двух слагаемых , то определитель может быть разложен на
сумму двух определителейСлайд 15 6. Определитель не изменится, если к элементам строки
(столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на
любое число
Слайд 16
Определения
Минором некоторого элемента aij n-го порядка называется определитель
порядка n-1, полученный из исходного вычёркиванием строки i и
столбца j.
Слайд 17
Определения
Алгебраическим дополнением некоторого элемента aij называется его минор,
взятый со знаком «+», если сумма i+j – чётное
число, и со знаком «минус» в противном случае.Аij = (-1)i+j mij