Слайд 2
Цель работы:
Изучить:
Биографию Пифагора.
Историю образования общества
пифагорейцев.
История доказательства теоремы.
Изучение теоремы в наши дни.
Применение теоремы.
Слайд 3
Задачи:
1.Воостановить основные этапы жизни и деятельности Пифагора.
2.Показать гениальность
теории Пифагора.
3.Выявить связь между теоремой Пифагора и теорией чисел.
4.Показать
практическую направленность теоремы Пифагора.
Слайд 4
Метод работы:
Поиск материала,
Анализ,
Наблюдение.
Слайд 5
Содержание:
1. Годы жизни Пифагора и его политическая
судьба.
2..Поздний брак.
3..Пифагорийская звезда.
4. Магия чисел
5.Формулировки теоремы.
6. Доказательство
теоремы:
7 Древняя натурфилософия.
8.Священная нумерология
9. Странности геометрии.
10.Совсем не простые простые числа.
11.Число имени.
12.Наука о числах и философия.
13. Пифагор в классном журнале.
14. Применение теоремы.
15 Значение теоремы Пифагора.
Слайд 6
Годы жизни Пифагора
Великий учёный
Пифагор родился около 570 г. до н. э. на
острове Самос.
Отцом Пифагора был Мнесарх, резчик по драгоценным камням.
Имя же матери Пифагора неизвестно.
По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил свои незаурядные способности.
Среди учителей юного Пифагора традиция называет имена старца Гермодаманта и Ферекида Сирийского (хотя и нет твёрдой уверенности в том, что именно Гермодаманта и Ферекид были первыми учителями Пифагора).
Неугомонному воображению юного Пифагора очень стало тесно на маленьком Самосе, и он отправляется в Милет, где встречается с другим ученым - Фалесом. Фалес советует отправиться за знаниями Египет, что Пифагор и сделал.
Слайд 7
После возвращения, он собирает вокруг себя юношей из
благородных семей и ведет с ними тайные беседы. Пифагор
учит:
« Посмотри вокруг себя. Везде в мире порядок, всё подчинено гармонии, мере. Даже звуки, и те подчинены числам. Везде в природе господствует порядок, установленный богами. Даже небесные светила и звезды подчиняются им. Как же может не подчиниться им человек? Горе тому городу, где царствует хаос, где все решает толпа, где нет почтения древнему строю.»
Слайд 8
Поздний брак.
Пифагор был высоким,
свыше 180 сантиметров ростом – хорошо сложенным мужчиной с
величественно осанкой, красавец с тонкими чертами лица. Однако свою юность и зрелость он посвятил наукам и женился, когда ему было примерно 60 лет. Его избранницей стала Феано, дочь Бронтина, одна из его учениц. Феона родила ему несколько детей: сыновей Телавга и Минесарха, дочерей Мию и Аригноту . Жена и дети являлись верными его последователями. Известно, что Феано была автором книги « О благочестии», а Телавг – «О тетракиде». Другие дети тоже сочиняли пифагорейские сочинения, но никаких подробностей о них не сохранилось.
Слайд 9
Излюбленной геометрической фигурой пифагорейцев был пентаграмм, называемый так
же пифагорейской звездой. Пифагорейцы пользовались этой фигурой, вычерчивая её
на песке, чтобы приветствовать и узнавать друг друга.
Слайд 10
Пифагор увлекался математикой и геометрией. Его теорема о
свойствах прямоугольного треугольника – самая древняя и самая известная
из геометрических теорем. Её создатель Пифагор вместе со своими последователями исключительно большое значение придавали математике. Но его представление о числах существенно отличалось от современных.
Описывает она свойства сторон прямоугольного треугольника.
Квадрат стороны, противолежащий прямоугольному углу – гипотенузы – равен сумме квадратов двух других сторон (катетов): а2 +в2=с2.
Согласно легенде, доказав теорему, Пифагор принёс в жертву богу быка, испечённого из пшеничной муки, или, как рассказывают другие, 100 быков.
Слайд 11
Приводим различные формулировки теоремы Пифагора в переводе с
греческого, латинского и немецкого языка. У Евклида эта теорема
гласит (дословный перевод): «В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол».
Латинский перевод арабского текста Аннаирици (около 900 л. до н.э.), сделанный Герхардом Клемонским (начало 12 в), в переводе на русский гласит: « Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол».
Слайд 12
В Geometria Culmonensis ( около 1400г.) в переводе
теорема читается так: «Итак, площадь квадрата, измеренного по длинной
стороне, столь же велика, как у квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу».
В первом русском переводе евклидовых «Начал», сделанном Ф. Петрушевским, теорема Пифагора изложена так: «В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол».
Слайд 13
В работе я привел доказательство теоремы:
а) доказательство
Евклида, упрощенное доказательство Евклида.
б) доказательство Хоукинса.
в)
Доказательство Вальдхейма
г) доказательство, основанное на теории подобия.
д) Луночки Гиппократа.
ж) векторное доказательство.
Слайд 14
Доказательство Вадьдхейма.
Это доказательство имеет вычислительный характер. Можно использовать
рисунки для доказательства основанного на вычислении площадей двумя способами.
Для того чтобы доказать теорему пользуясь первым рисунком достаточно только выразить площадь трапеции двумя путями. Sтрапеции = (a+b)²/2 и Sтрапецииa²b²+c²/2
Приравнивая правые части получим: a²+ b² = c²
Теорема доказана.
Слайд 15
Векторное доказательство.
Пусть АВС - прямоугольный треугольник с прямым
углом при вершине С, построенный на векторах. Тогда справедливо
векторное равенство: b + c = a откуда имеем c = a – b
возводя обе части в квадрат, получим c²=a²+b²-2ab Так как a перпендикулярно b, то ab=0, откуда
возводя обе части в квадрат, получим c²=a²+b²-2ab.Так как a перпендикулярно b, то ab=0, откуда c²=a²+b² или c²=a²+b². Нами снова доказана теорема Пифагора.
Если треугольник АВС - произвольный, то та же формула дает т. н. теорему косинусов, обобщающую теорему Пифагора.
Слайд 16
Древняя натурфилософия.
Но достижения Пифагора не сводились к теореме,
названной его именем
Пифагор утверждал, что всё рождается не
из числа, а согласно числу, то есть оно не являлось источником сущего, но выражала его связь с вторичными, третичными и так далее явлениями мира.
Позже идеи Пифагора весьма повлияли на формирование философии Платона.
Слайд 17
Священная нумерология
Пифагор видел числа везде и во
всем связывал с ними все вещи и явления внешнего
мира. Так, например, четные числа, не делящиеся пополам без остатка, он считал «совершенными»; ибо они «конечные», и неделимые. Вещи, которые можно без остатка разделить пополам, и, следовательно, обладавшие противоположные качествами, они связывали с четными числами.
Слайд 18
Странности геометрии.
Пифагорейцы считали основой всех математических наук
арифметику. Многим было приятно узнать, например, что если ликвидировать
геометрию, арифметика не пострадает, и наоборот, геометрия без арифметики жить не может.
Геометрические фигуры можно выстраивать из точек и создавать из них интересные
Слайд 19
Пифагорейцы обнаружили, что множители чисел 220 (1,2,4,5,10,11,20,44,55,110) и
284 (1,2,4,71,142) дают в сумме соответственно 284 и 220,
и назвали эти числа «дружественными».
Пифагор вычислил, что сумма углов треугольника равна 180 градусам, а также первый открыл существование иррациональных чисел.
Слайд 20
Простые числа не были для приверженцев учения Пифагора
только материалом для четырёх действий арифметики. Они имели скрытый
смысл.
1 - число энергии, действия, причины (потому что оно в начале), достижения цели (в собственных интересах).
2 - число противоположностей, полярностей, таких как день и ночь, добро и зло, мальчик и девочка... В зависимости от ситуации, противоположности могут конфликтовать - спорить и соперничать, или же дополнять друг друга, поддерживая состояние равновесия.
Слайд 21
6 - это число пифагорейцы называли "совершенством" и
"гармонией". Оно связано также со здоровьем и равновесием (поскольку
состоит из двух троек).
7 - с этим числом связаны семь цветов радуги, семь нот гаммы, семь планет, известных древним грекам, - то есть явления неординарные, 7 - число случая, удачи и откровения свыше.
Слайд 22
В прежние времена существовали алфавиты, где буквы одновременно
являлись числами. Таким был и родной алфавит Пифагора, древнегреческий.
Каждая буква имела не только цифровое выражение, но и своё особое имя и отдельный смысл. Считается, кстати, что скрытое значение буквы ипсилон первым понял Пифагор (это вторая буква его имени).
Слайд 23
Обрывки средневековой нумерологии долетели до наших дней. В
современном варианте она больше напоминает игру. Можно, например, взять
и высчитать число своего имени.
Возьмём, например, имя Фёкла. Букве "Ф" соответствует в таблице число 4; букве "ё" - 7; "к" - 3; "л" - 4; "а" - 1. Складываем: 4+7+3+4+1=19. Эта сумма не укладывается в ряд простых чисел. Поэтому складываем ещё единицу и девятку. Получаем 10. 1+0=1. Стало быть, число имени Фёкла - единица. Согласно науке о числах, его должна носить энергичная особа с далеко идущими планами. Подобную процедуру можно проделать с любым именем.
Слайд 24
Пифагор в классном журнале
Люди, проникшиеся хотя бы отчасти
учением Пифагора о числах, легко откроют для себя подлинный
смысл школьных отметок.
Ставить единицу учителя как-то стесняются. Единица в журнале не огорчает, а изумляет, как некое потустороннее явление.
Двойка неудобна тем, что её надо исправлять. Это обстоятельство делает её непопулярной. Пифагорейцы тоже не очень её любили - за, соответственно, двойственность. Эта отметка прямо указывает на полярность, противостояние, конфликт: ты по одну сторону баррикад, а наука - по другую.
Слайд 25
Тройка занимает промежуточное положение между очевидным незнанием, которое
символизирует двойка, и твёрдым знанием, которое подтверждает четвёрка. Она
указывает на соглашательскую позицию педагога: "Ступай, мол, с миром, не будем ссориться". Если по некоему предмету у человека за всю четверть не набирается иных отметок, кроме двойки и четвёрки, учитель, подводя итоги, может выставить ему среднее арифметическое: примиренческую тройку. Дескать, была охота связываться...
Рисуя против твоей фамилии четвёрку, преподаватель подразумевает, что основная информация тобою усвоена. Четвёрка означает, что твой рейтинг, с его точки зрения, устойчив. В то же время, число это настолько стабильно, что его неохота менять. Чтобы вышла пятёрка, к четвёрке надо прибавить единицу. То есть для того, чтобы заделаться отличником, требуется дополнительная энергия.
Слайд 26
Получая пятёрку, ты приобщаешься к кругу избранных. То
есть к статусу простого смертного, существующего, как все, среди
четырёх стихий и четырёх сторон света (4), ты прибавляешь привилегии небожителя (1) - особое отношение со стороны окружающих.
Подобным образом можно изучать цены в магазине, или номера машин, или телефонные номера.
Слайд 27
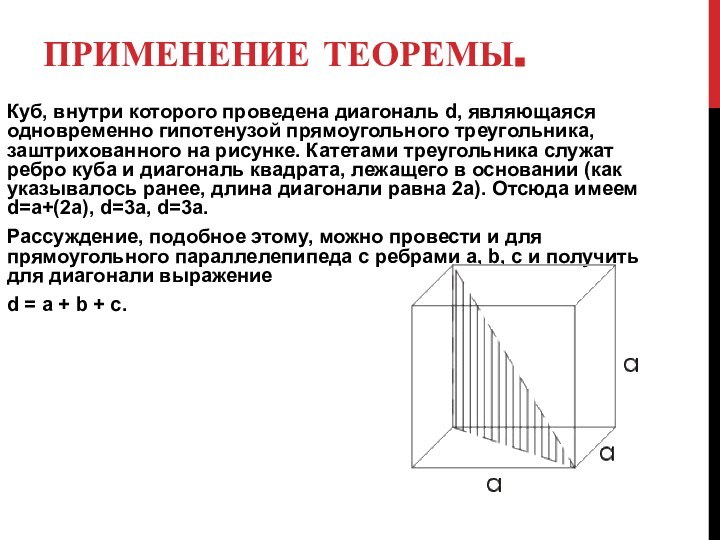
Применение теоремы.
Куб, внутри которого проведена диагональ d, являющаяся
одновременно гипотенузой прямоугольного треугольника, заштрихованного на рисунке. Катетами треугольника
служат ребро куба и диагональ квадрата, лежащего в основании (как указывалось ранее, длина диагонали равна 2а). Отсюда имеем d=a+(2a), d=3a, d=3a.
Рассуждение, подобное этому, можно провести и для прямоугольного параллелепипеда с ребрами a, b, с и получить для диагонали выражение
d = a + b + c.
Слайд 28
"Чтобы найти поверхность крыши, все скаты которой имеют
равный уклон, нужно умножить перекрываемую площадь на длину какого-нибудь
стропила и разделить полученное произведение на проекцию этого стропила ??? на перекрываемую площадь."
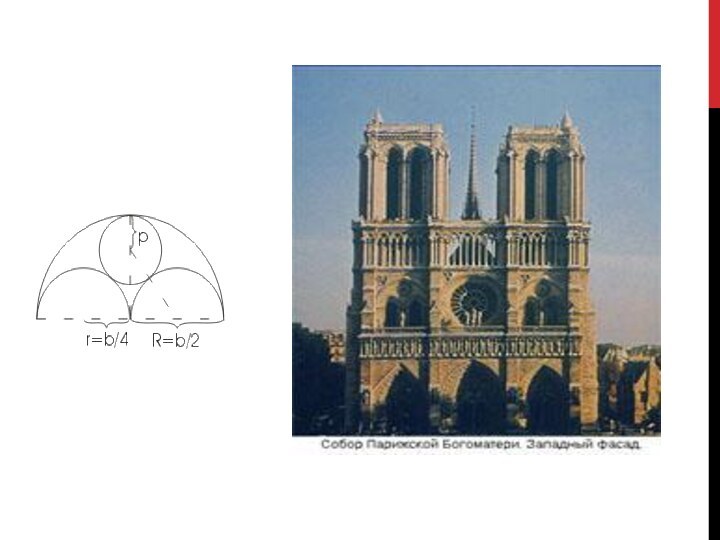
В зданиях готического и ромaнского стиля верхние части окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон. На рисунке представлен простой пример такого окна в готическом стиле. Способ построения его очень прост: Из рисунка легко найти центры шести дуг окружностей, радиусы которых равны
ширине окна (b) для наружных дуг
половине ширины, (b/2) для внутренних дуг
Остается еще полная окружность, касающаяся четырех дуг Т. к. она заключена между двумя концентрическими окружностями, то ее диаметр равен расстоянию между этими окружностями, т. е. b/2 и, следовательно, радиус равен b/4. А тогда становится ясным и положение ее центра.
Слайд 30
Доказательство теоремы Пифагора учащиеся средних веков считали очень
трудным и называли его ослиный мост, бегство «убогих», так
как некоторые убогие ученики, не имевшие серьёзной математической подготовки, бежали от геометрии. Слабые ученики, заучившие теоремы наизусть, без понимания, и прозванные поэтому «ослами», были в не состоянии преодолеть теорему Пифагора, служившего для них вроде непреодолимого моста. Из-за чертежей, сопровождающих теоремы Пифагора, учащиеся называли её также «ветряной мельницей», составляли стихи вроде «Пифагоровы штаны на все стороны равны», и рисовали карикатуры