- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Пирамида
Содержание
- 2. Цель изучения темы: овладение системой математических знаний и умений, необходимых для применения в практической деятельности
- 3. Интеллектуальное развитие, формирование качеств личности: ясность и точность мыли, логическое мышление, элементы алгоритмической культуры, пространственных представлений
- 4. воспитание культуры личности, отношения к математике как
- 5. В ходе ее достижения решаются задачи: изучение
- 6. Содержание темы по учебнику «Геометрия, 10-11 », автор Л.С. Атанасян.
- 7. Место в учебнике Глава 4. Многогранники (18 часов)Понятие многогранника. Призма. Пирамида. Правильные многогранники
- 8. Методы и приемы, используемые при обучении темы:
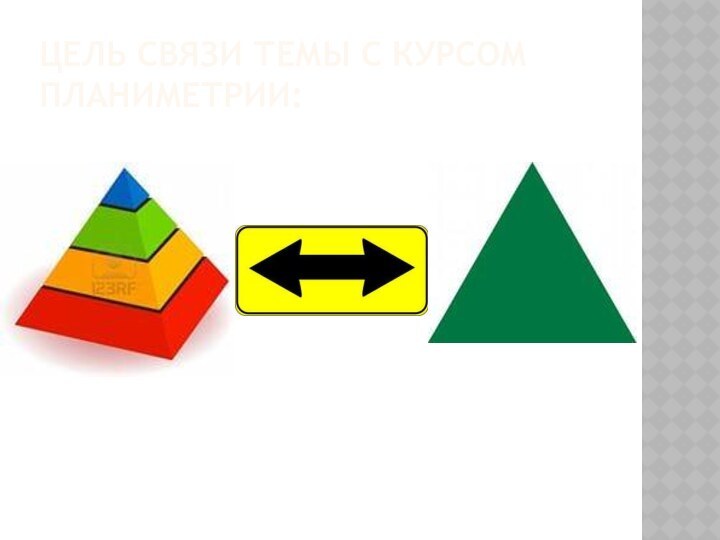
- 10. Требования к уровню подготовки обучающихся
- 11. Тема: ПирамидаЗнать: понятия пирамиды
- 12. Тема: Правильная пирамидаЗнать: понятия правильной пирамиды и
- 13. Тема: Усечённая пирамидаЗнать: понятия усеченной пирамиды и
- 14. Обобщающий урок по теме: Пирамида. Решение задач.Знать:
- 15. Вопросы, связанные с изучением курса планиметрии:
- 16. При изучении понятия правильной пирамиды целесообразно вспомнить,
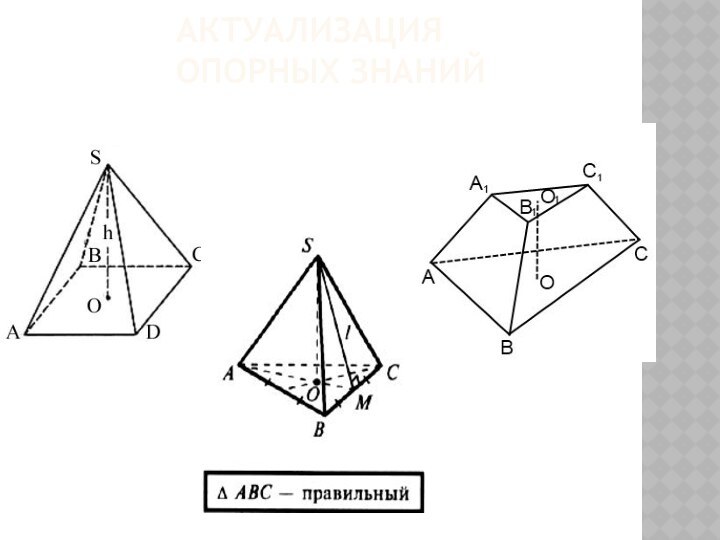
- 17. Цель связи темы с курсом планиметрии:
- 18. Развить пространственное воображение школьников;Учиться использовать при решении
- 19. Уметь изображать пирамиду, правильную пирамиду, усеченную пирамиду.
- 20. УрокТип урока: урок обобщения и систематизации.Вид урока: урок-практикум.Метод проведения урока: частично-поисковый.
- 21. Структура урока: Организационный момент.Актуализация опорных знаний.Практическое применение пирамиды.Самостоятельная работа.Подведение итогов урока.
- 22. Актуализация опорных знаний
- 23. Практическое применение пирамиды
- 24. Любителям географии
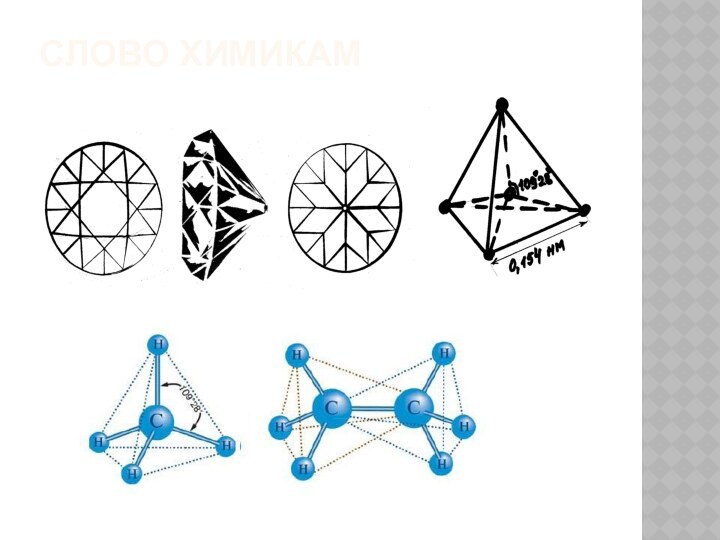
- 25. Слово химикам
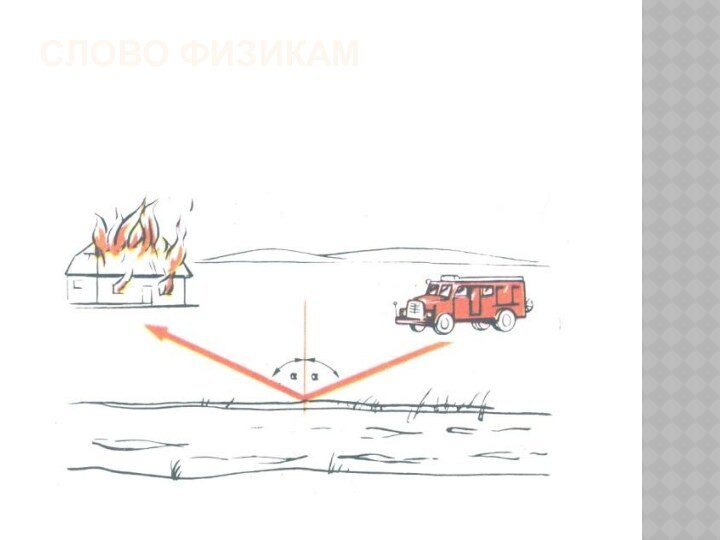
- 26. Слово физикам
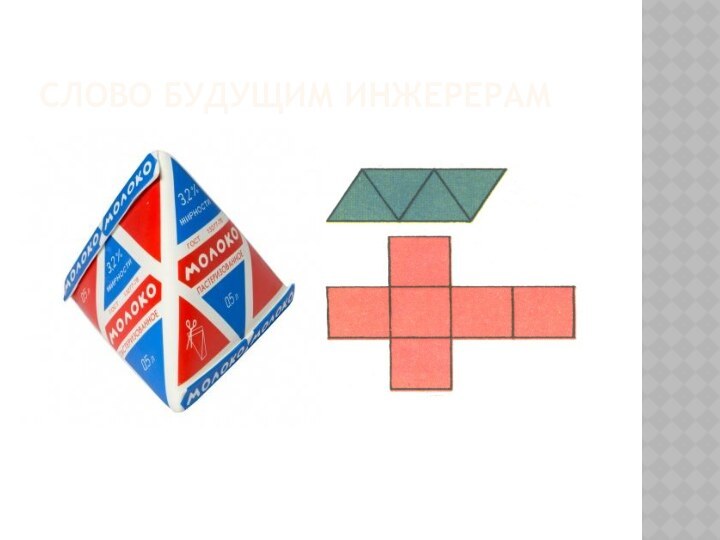
- 27. Слово будущим инжерерам
- 28. Слово будущим архитекторам
- 29. Заполни таблицу
- 32. Контрольная работа
- 34. Критерии и нормы оценки контрольной работ по
- 35. Не грубыми ошибками считаются ошибки, допущенные в
- 36. Скачать презентацию
- 37. Похожие презентации
Цель изучения темы: овладение системой математических знаний и умений, необходимых для применения в практической деятельности





























Слайд 2
Цель изучения темы:
овладение системой математических
знаний и умений, необходимых для применения в практической деятельности
Слайд 3 Интеллектуальное развитие, формирование качеств личности: ясность и точность
мыли, логическое мышление, элементы алгоритмической культуры, пространственных представлений
Слайд 4 воспитание культуры личности, отношения к математике как к
части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса
Слайд 5
В ходе ее достижения решаются задачи:
изучение свойств пространственных
тел
формирование умения применять полученные знания для решения практических задач.
Слайд 7
Место в учебнике
Глава 4. Многогранники (18
часов)
Понятие многогранника.
Призма.
Пирамида.
Правильные многогранники
Слайд 8
Методы и приемы, используемые при обучении темы:
принципы технологии
уровневой дифференциации;
подача материала блоками;
объяснительно-иллюстративный;
обучение с применением опорных схем;
Слайд 11
Тема: Пирамида
Знать: понятия пирамиды и
ее элементов, площади боковой поверхности и полной поверхности пирамиды.
Уметь:
решать задачи по теме.
Слайд 12
Тема: Правильная пирамида
Знать: понятия правильной пирамиды и ее
элементов; теорему о площади боковой поверхности правильной пирамиды с
доказательством.Уметь: решать задачи по теме.
Слайд 13
Тема: Усечённая пирамида
Знать: понятия усеченной пирамиды и ее
элементов, правильной усеченной пирамиды и ее апофемы; доказательство того,
что боковые грани усеченной пирамиды – трапеции; формулу площади боковой поверхности усеченной пирамиды.Уметь: решать задачи по теме
Слайд 14
Обобщающий урок по теме: Пирамида. Решение задач.
Знать: понятия
пирамиды и ее элементов, правильной и усеченной пирамиды и
их элементов; формулы площади боковой и полной поверхности пирамиды, площади боковой поверхности правильной и усеченной пирамидыУметь: решать задачи по теме.
Слайд 16 При изучении понятия правильной пирамиды целесообразно вспомнить, какой
многоугольник называется правильным?
Высота проецируется в центр основания многогранника. Что
называется центром основания многогранника? Что будет являться центром треугольника? квадрата? параллелограмма?Вспоминаем площади многоугольников. Это понадобится нам при нахождении площади поверхностей пирамиды
Слайд 18
Развить пространственное воображение школьников;
Учиться использовать при решении стереометрических
задач планиметрические факты и методы;
Ввести понятие пирамиды, правильной пирамиды,
апофемы, усеченной пирамиды, площадей полной и боковой поверхностей.
Вывести формулы площадей полной и боковой поверхностей.
Слайд 19 Уметь изображать пирамиду, правильную пирамиду, усеченную пирамиду. Отличать
правильную пирамиду от тетраэдра.
Анализировать взаимное расположение объектов в пространстве
Закрепить
навыки решения задач о пирамидах.Формировать умения осуществлять самоконтроль в процессе самостоятельной работы
Слайд 20
Урок
Тип урока: урок обобщения и систематизации.
Вид урока:
урок-практикум.
Метод проведения урока: частично-поисковый.
Слайд 21
Структура урока:
Организационный момент.
Актуализация опорных
знаний.
Практическое применение пирамиды.
Самостоятельная работа.
Подведение итогов урока.
Слайд 34
Критерии и нормы оценки контрольной работ по математике
При
оценке письменных работ по математике «грубой» ошибкой следует считать:
неверное выполнение вычислений в следствие неточного применения правил,
неправильное решение задачи (неправильный выбор или пропуск действий, выполнение ненужных действий, искажение смысла вопроса, привлечение посторонних или потеря необходимых числовых данных),
неумение правильно выполнить измерение и построение геометрических фигур.
Слайд 35 Не грубыми ошибками считаются ошибки, допущенные в процессе
списывания числовых данных (искажения, замена), знаков арифметических действия, нарушения в
формулировке вопроса (ответа), правильность расположения записей, чертежей, небольшая неточность в измерении и черчении.Оценка не снижается за грамматические ошибки, допущенные в работе. Исключения составляют случаи написания этих слов и словосочетаний, которые используются на уроке математики (названия компонентов и результатов действий, величин и т.д.).