- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Понятия теории графов
Содержание
- 2. Граф И ЕГО СВОЙСТВА ПРИМЕРЫ ГРАФОВ
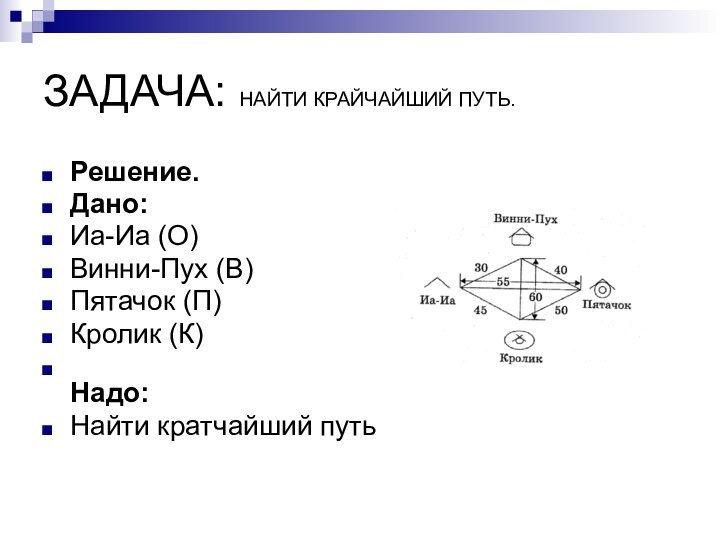
- 3. ЗАДАЧА: НАЙТИ КРАЙЧАЙШИЙ ПУТЬ.Решение.Дано:Иа-Иа (О)Винни-Пух (В)Пятачок (П)Кролик (К) Надо:Найти кратчайший путь
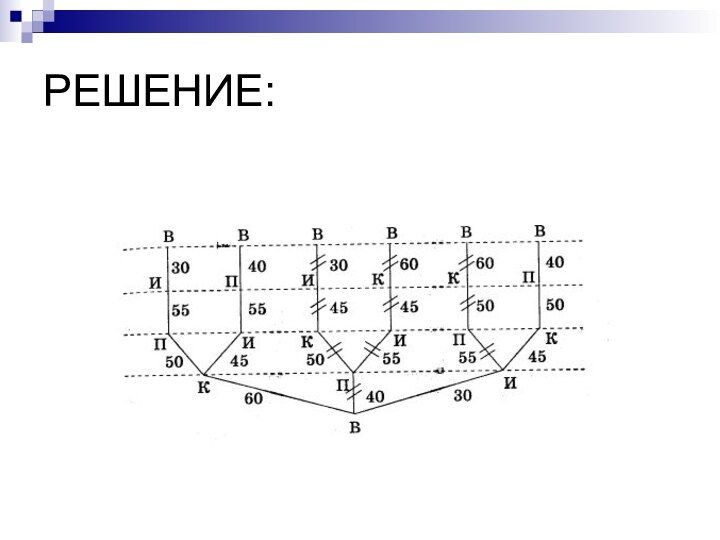
- 4. РЕШЕНИЕ:
- 5. ГРАФЫВершины ГРАФАРЕБРА ГРАФАНУЛЕВОЙ ГРАФ НЕПОЛНЫЙ ГРАФ
- 6. ЗАКОНОМЕРНОСТИ СТЕПЕНЬ ВЕРШИНЫ1) Степени вершин полного графа
- 7. Кенигсбергские мосты 1)
- 8. Путь в графе. Цикл. Путем в графе … конец пути… Циклом Эйлеровой линией
- 9. Связные графы. Две вершины графа называются связными
- 10. ДЕРЕВЬЯДеревом НАЗЫВАЕТСЯВсякое ребро в дереве является мостом.
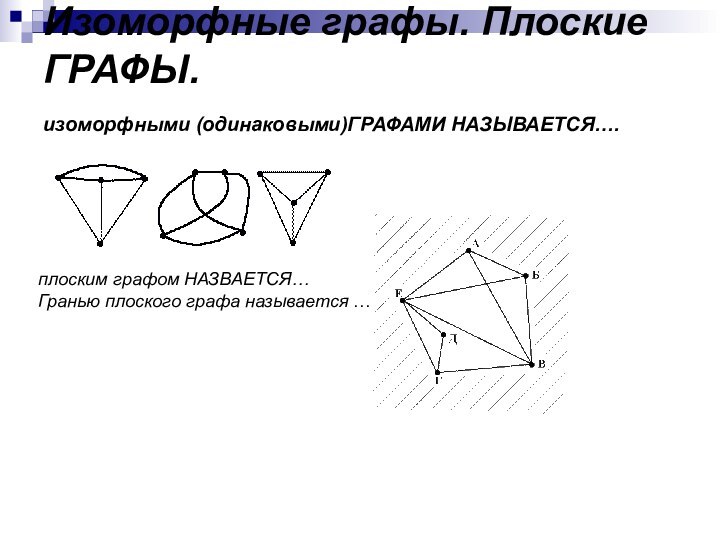
- 11. Изоморфные графы. Плоские ГРАФЫ. изоморфными (одинаковыми)ГРАФАМИ НАЗЫВАЕТСЯ…. плоским графом НАЗВАЕТСЯ…Гранью плоского графа называется …
- 12. Скачать презентацию
- 13. Похожие презентации
Граф И ЕГО СВОЙСТВА ПРИМЕРЫ ГРАФОВ

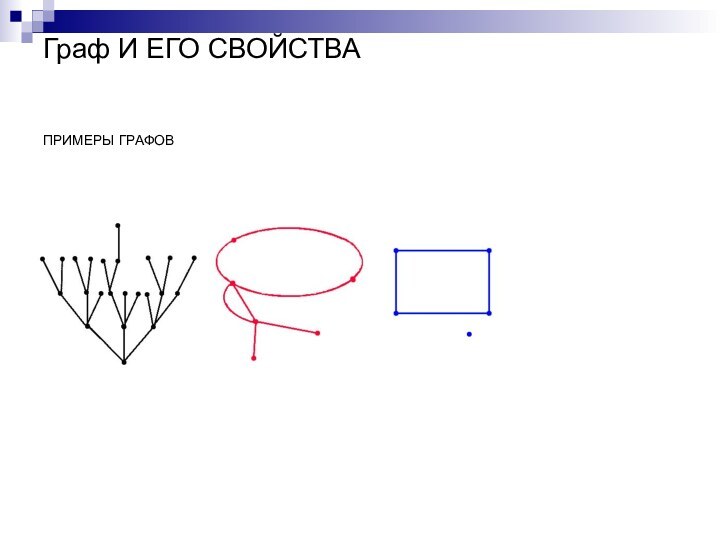



Слайд 3
ЗАДАЧА: НАЙТИ КРАЙЧАЙШИЙ ПУТЬ.
Решение.
Дано:
Иа-Иа (О)
Винни-Пух (В)
Пятачок (П)
Кролик (К)
Надо:
Найти
кратчайший путь
Слайд 5
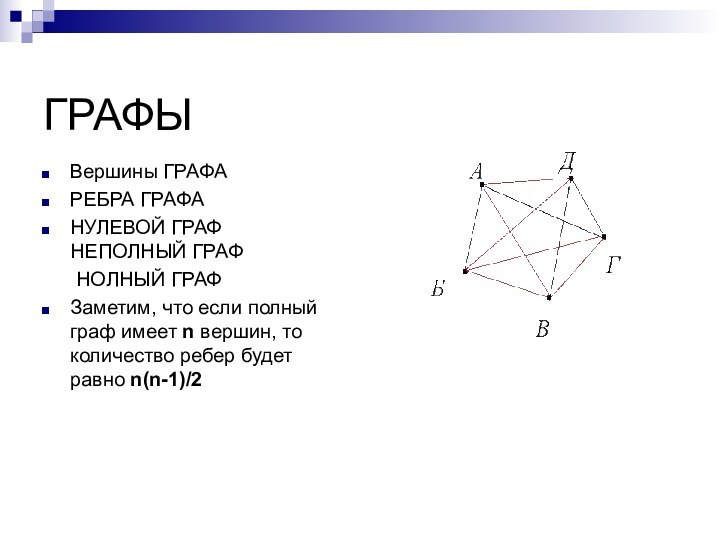
ГРАФЫ
Вершины ГРАФА
РЕБРА ГРАФА
НУЛЕВОЙ ГРАФ
НЕПОЛНЫЙ ГРАФ
НОЛНЫЙ
ГРАФ
Заметим, что если полный граф имеет n вершин, то
количество ребер будет равно n(n-1)/2
Слайд 6
ЗАКОНОМЕРНОСТИ
СТЕПЕНЬ ВЕРШИНЫ
1) Степени вершин полного графа одинаковы,
и каждая из них на 1 меньше числа вершин
этого графа.2) Сумма степеней вершин графа число четное, равное удвоенному числу ребер графа. Эта закономерность справедлива не только для полного, но и для любого графа.
Число нечетных вершин любого графа четно.
Слайд 7 Кенигсбергские мосты 1) Невозможно начертить граф с
нечетным числом нечетных вершин. 2) Если все вершины графа
четные, то можно не отрывая карандаш от бумаги («одним росчерком»), проводя по каждому ребру только один раз, начертить этот граф. Движение можно начать с любой вершины и закончить его в той же вершине 3) Граф, имеющий всего две нечетные вершины, можно начертить, не отрывая карандаш от бумаги, при этом движение нужно начать с одной из этих нечетных вершин и закончить во второй из них. 4) Граф, имеющий более двух нечетных вершин, невозможно начертить «одним росчерком». Фигура (граф), которую можно начертить не отрывая карандаш от бумаги, называется уникурсальной.
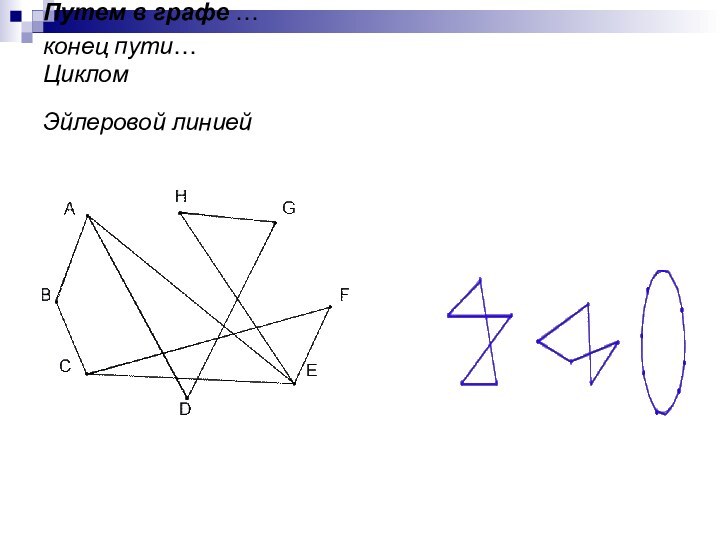
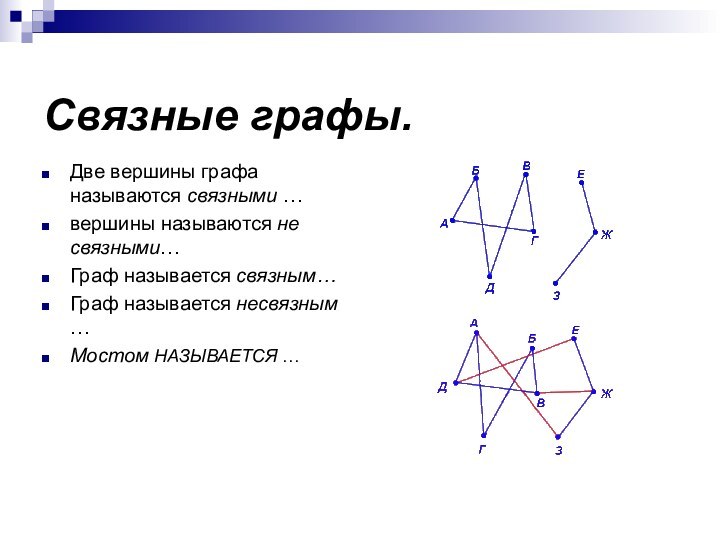
Слайд 9
Связные графы.
Две вершины графа называются связными …
вершины
называются не связными…
Граф называется связным…
Граф называется несвязным …
Мостом
НАЗЫВАЕТСЯ …
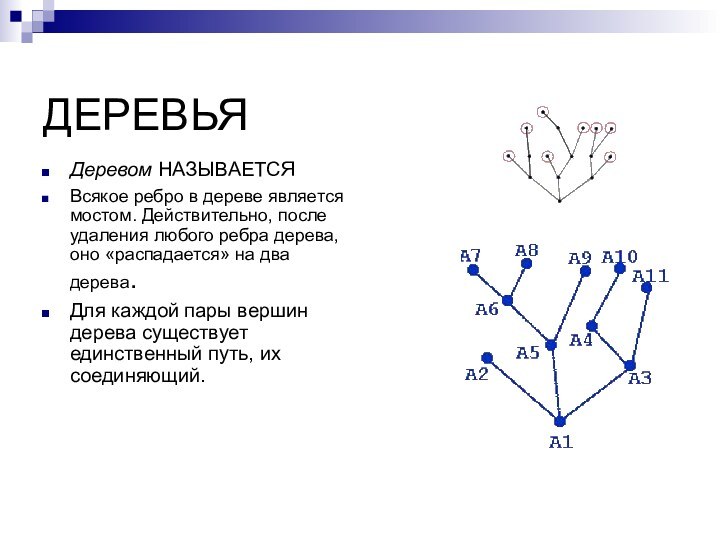
Слайд 10
ДЕРЕВЬЯ
Деревом НАЗЫВАЕТСЯ
Всякое ребро в дереве является мостом. Действительно,
после удаления любого ребра дерева, оно «распадается» на два
дерева.Для каждой пары вершин дерева существует единственный путь, их соединяющий.