Презентация на тему Построение графиков функций

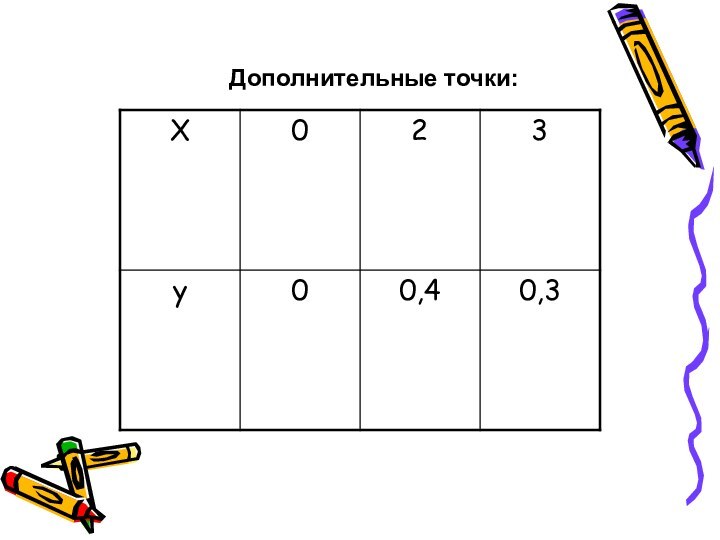
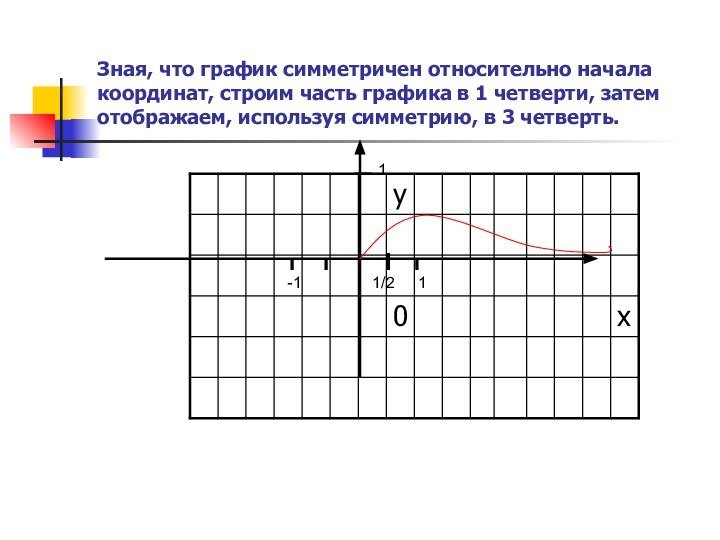
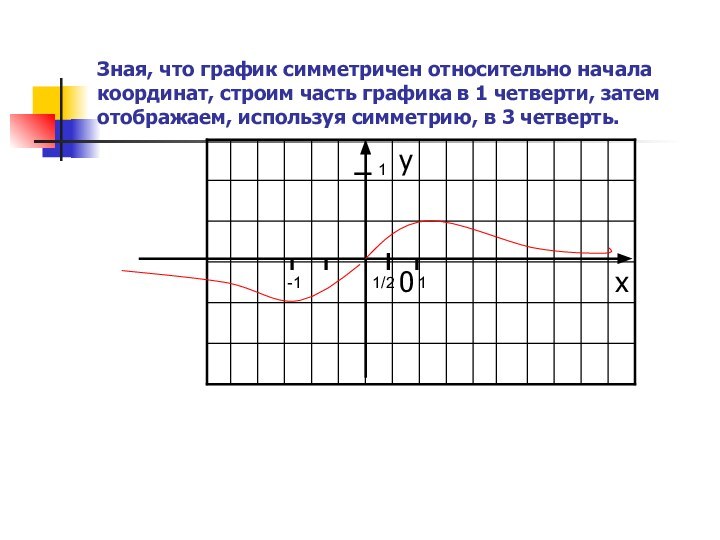
и критические точки;
- точки экстремума;
- точки пересечения графика с

осями координат;
- точки разрыва функции.
2. Проведя исследование функции, построить график.

Цели: изучив данный учебный элемент, вы сможете:

1. Учебник. – М., 2008.
Мордкович А.Г. Алгебра и начала

математического анализа. Часть 2. Задачник. – М., 2008.
Колмогоров А.Н. Алгебра и начала анализа. М., 2008.
Энциклопедический словарь юного математика. – М., 1989.

Литература

стационарные и критические точки;
Найти точки экстремума;
Найти промежутки монотонности;
Найти точки

пересечения с осями координат;
При необходимости найти дополнительные точки.

Схема исследования функции:

функции это все допустимые значения аргумента: D(у) = (-∞;

+∞).
2. Исследуем функцию на чётность:
у(х) = у(-х) – условие чётности, у(-х) = - у(х) – условие нечётности.

у(х) =


у(-х) =

= -у(х)

Выполняется условие нечётности, значит график симметричен относительно начала координат.

часть графика в 1 четверти, затем отображаем, используя симметрию,

в 3 четверть.

1/2

1

-1

1

часть графика в 1 четверти, затем отображаем, используя симметрию,

в 3 четверть.

1/2

1

-1

1

экстремума, б) стационарные точки, в) критические точки.

2. Точки, в

которых производная равна нулю это
а) точки экстремума, б) стационарные точки, в) критические точки.

3. у(х) = у(-х) это условие
а) чётности, б) нечётности, в) возрастания функции.

4. Если функция нечётная, то график симметричен относительно
а) оси ОУ, б) оси Ох, в) начала координат.

5.

х

+

-

---

1

2

0

3

Указать промежутки возрастания.

а) (0; 1) и (2;3), б) [1;2), в) (1;2)