- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Построение графиков функций и уравнений, содержащих переменную под знаком модуля
Содержание
- 2. Тема урока: «Построение графиков функций и уравнений, содержащих переменную под знаком модуля»
- 3. Тип урока: «Урок
- 4. Технология урока Проектная деятельность, интегрированный урок (математика + информатика).
- 5. Задачи: актуализация знаний о графиках функций и
- 6. Основная цель урока чтобы учащиеся
- 7. РефлексияЛинейная функцияТригонометрическая функцияКвадратичная функцияУ=f(|x|)|У|=f(x)У=|f(x)|Задание классувопрос классуДомашнее задание
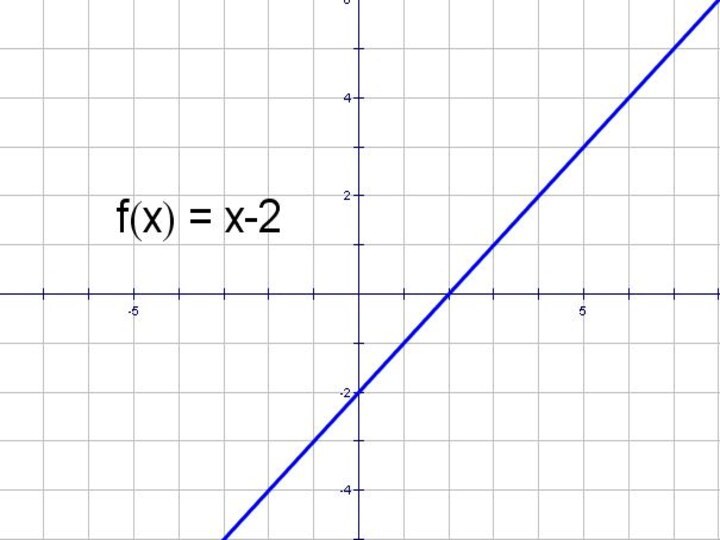
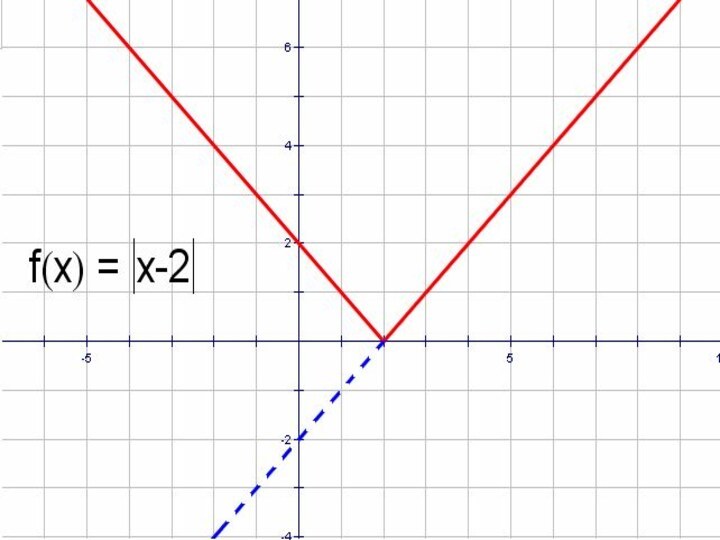
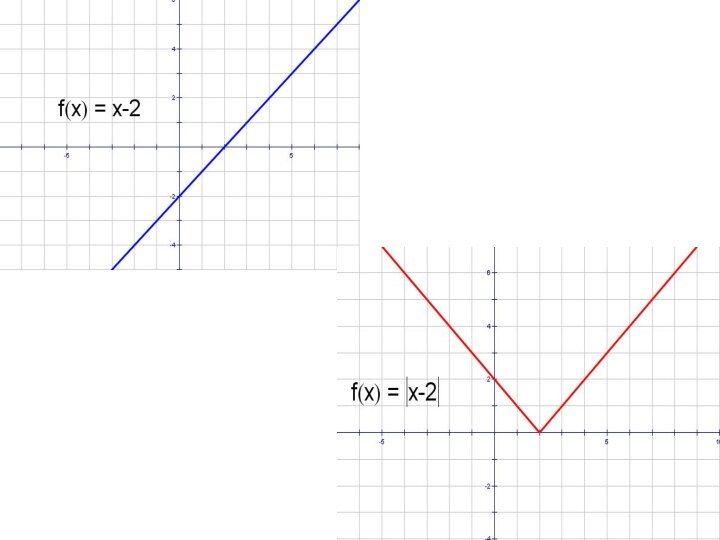
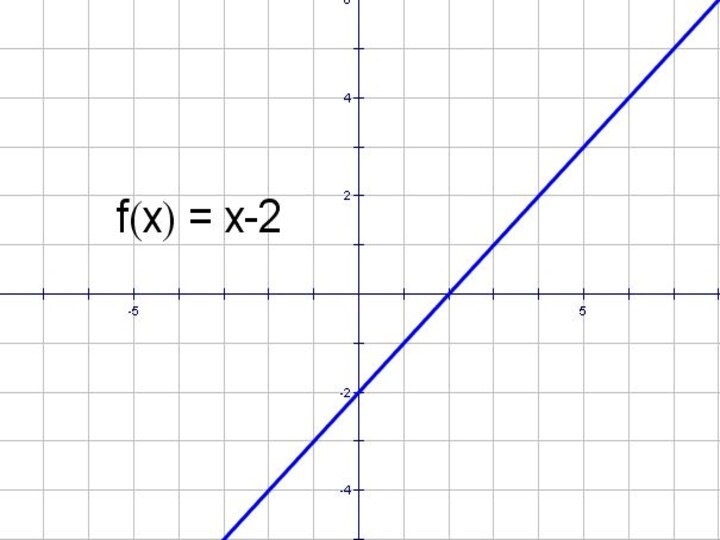
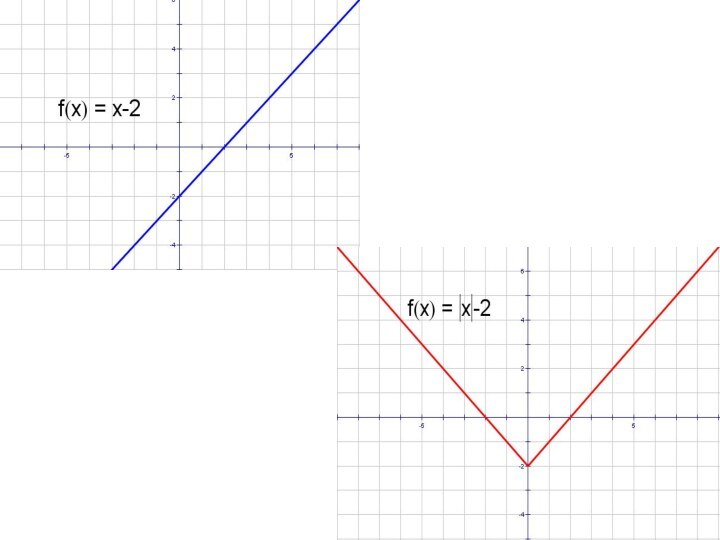
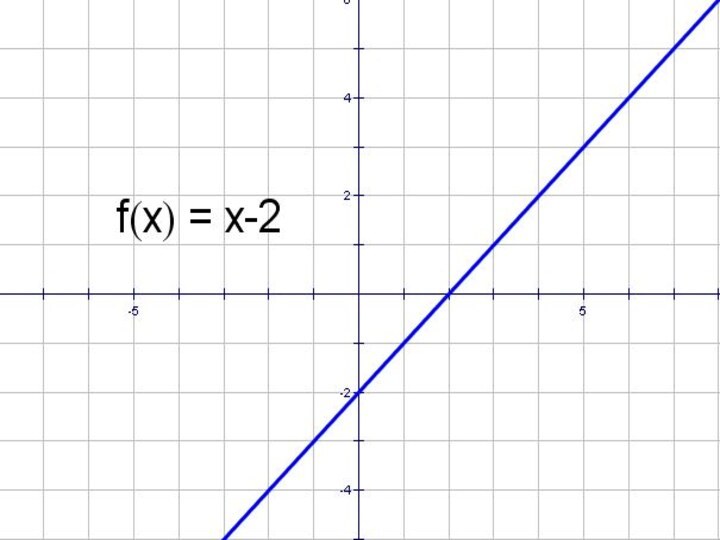
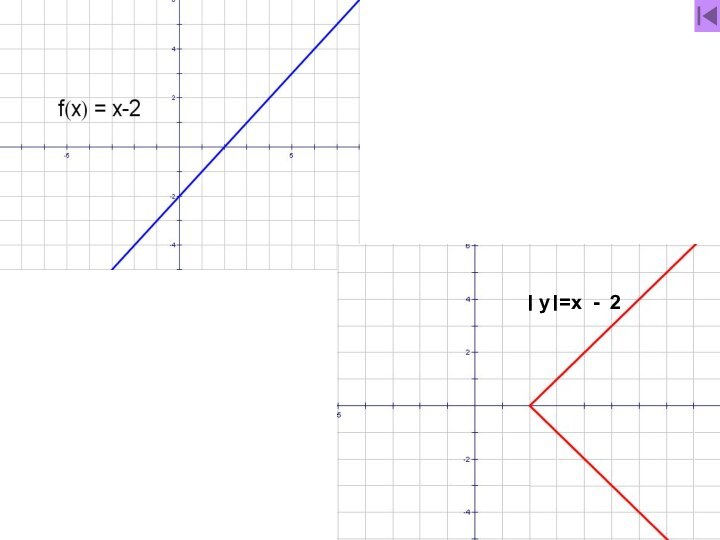
- 8. y = x – 2 и y =│x - 2│
- 12. y = x – 2 и y =│x│– 2
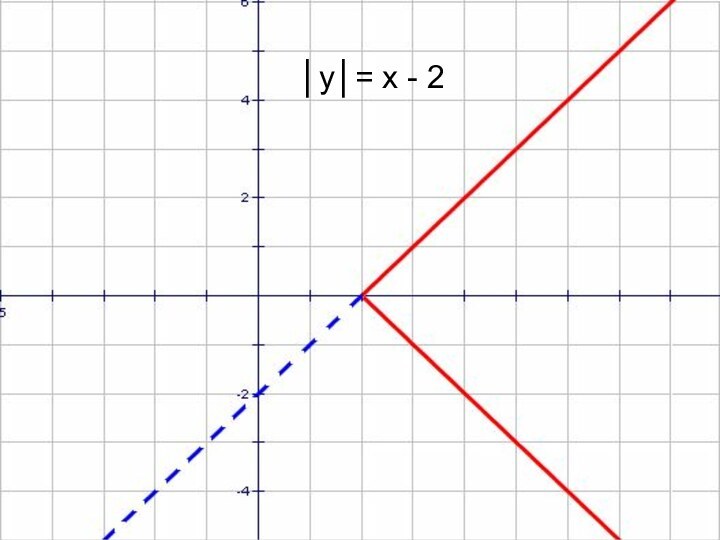
- 16. y = x – 2 и │y│= x - 2
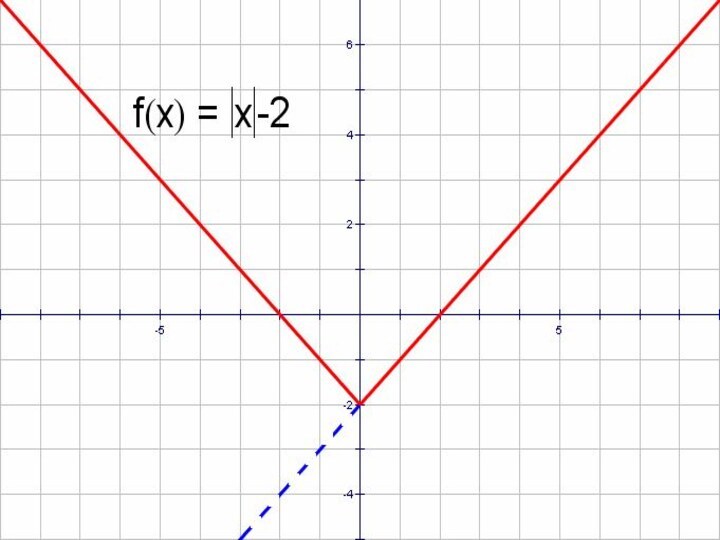
- 18. │y│= x - 2
- 19. । y।=x - 2
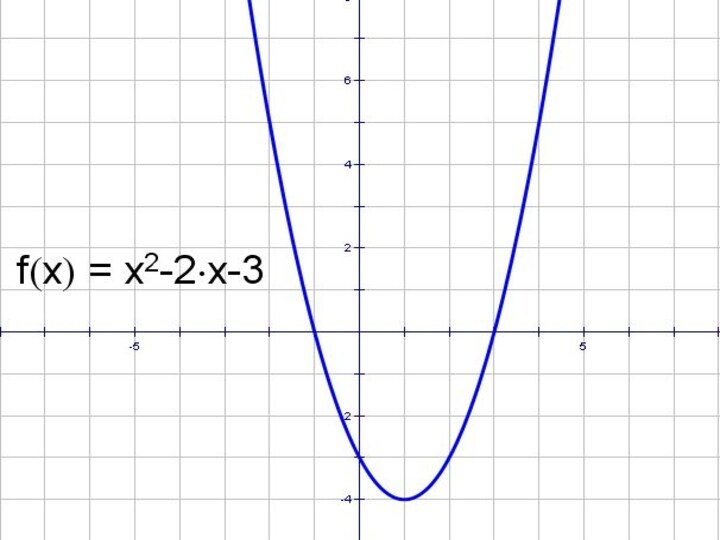
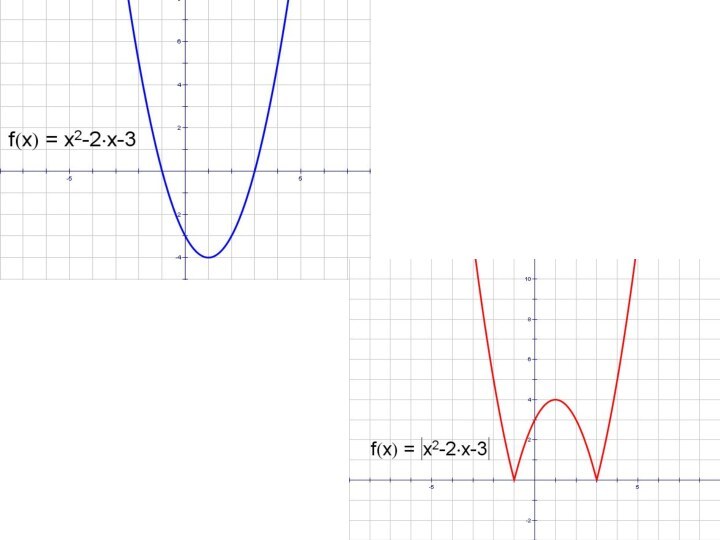
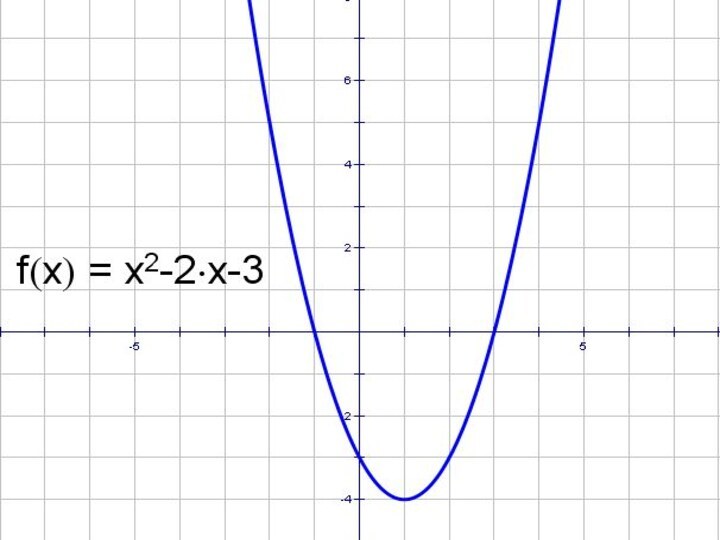
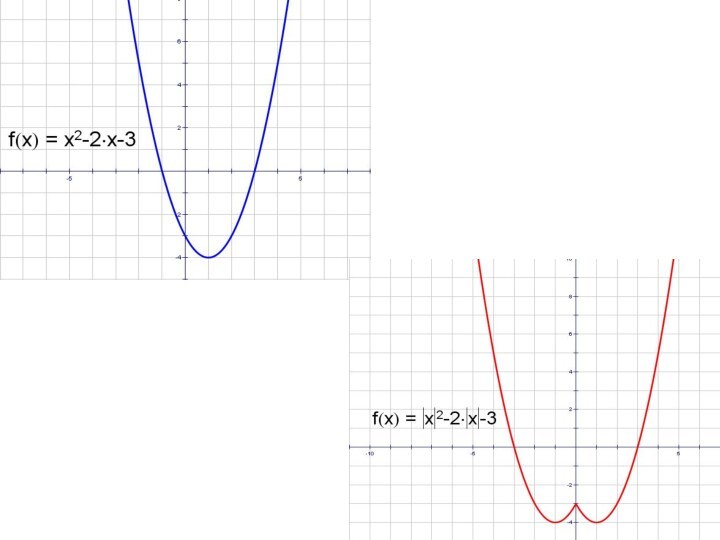
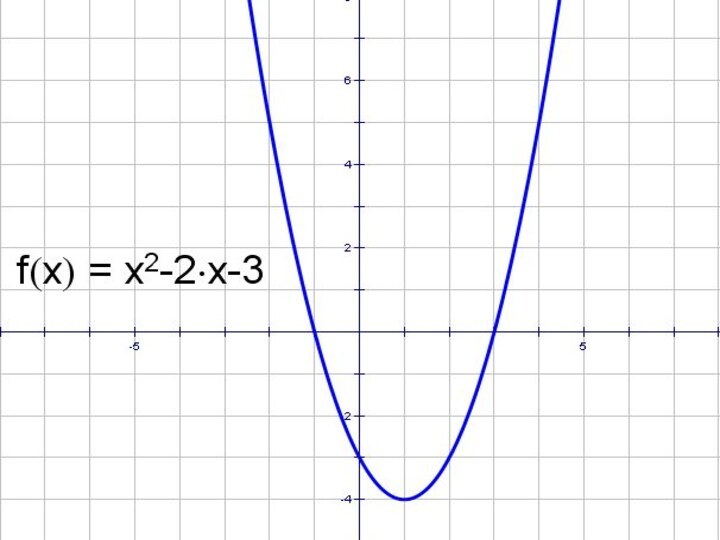
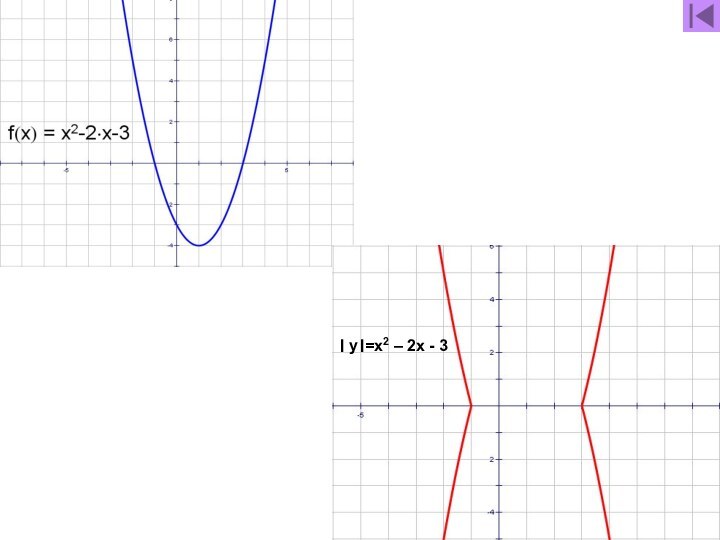
- 20. y = x2 – 2x – 3
- 24. y = x2 – 2x – 3
- 28. y = x2 – 2x –
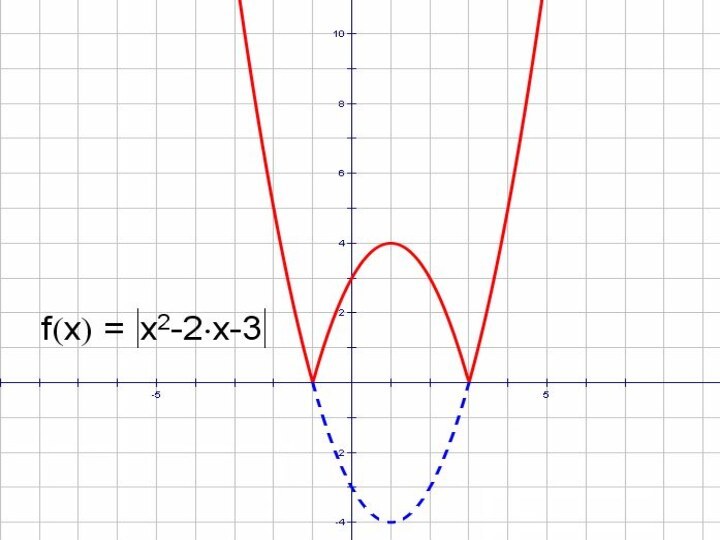
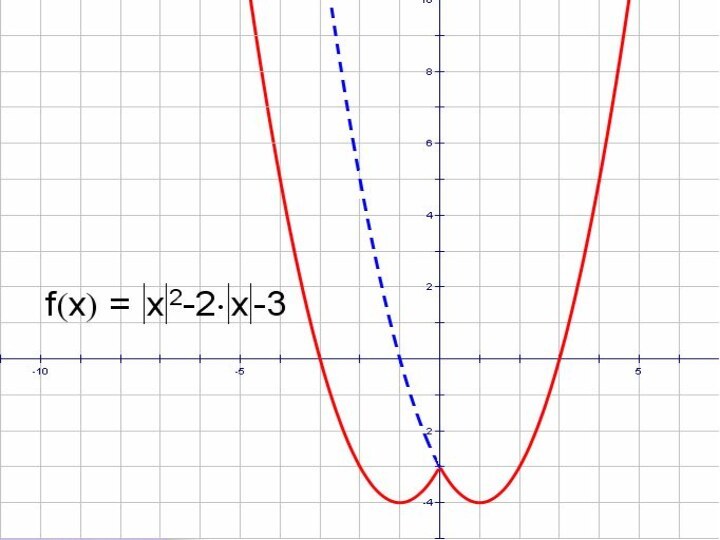
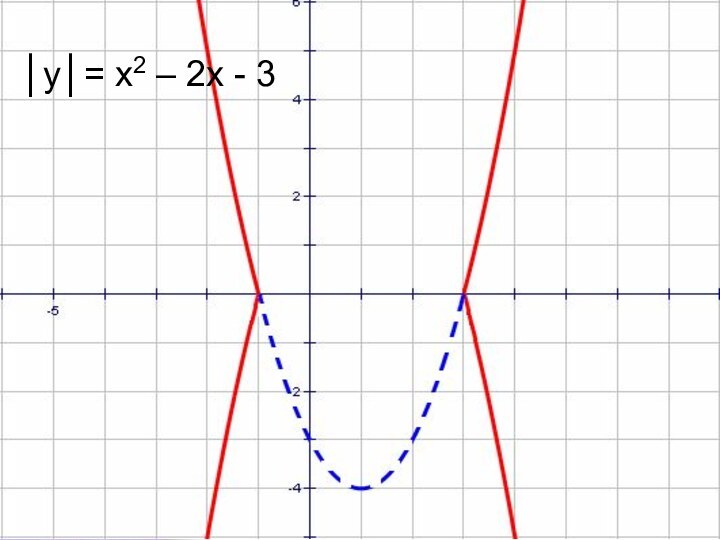
- 30. │y│= x2 – 2x - 3
- 31. । y।=x2 – 2x - 3
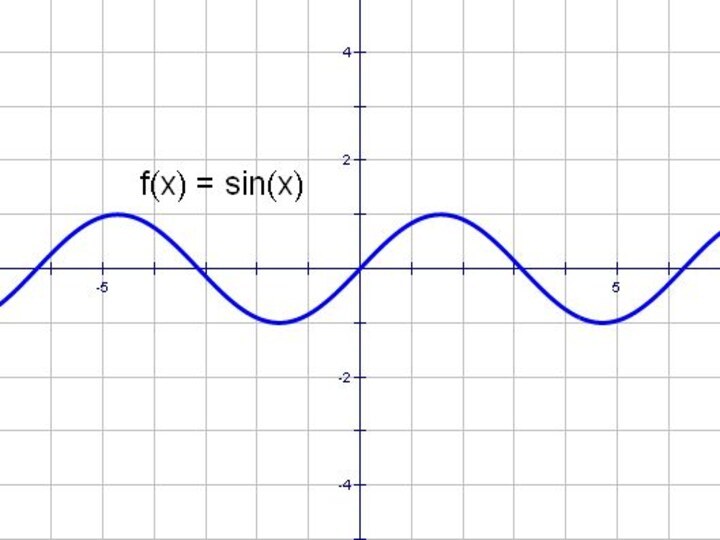
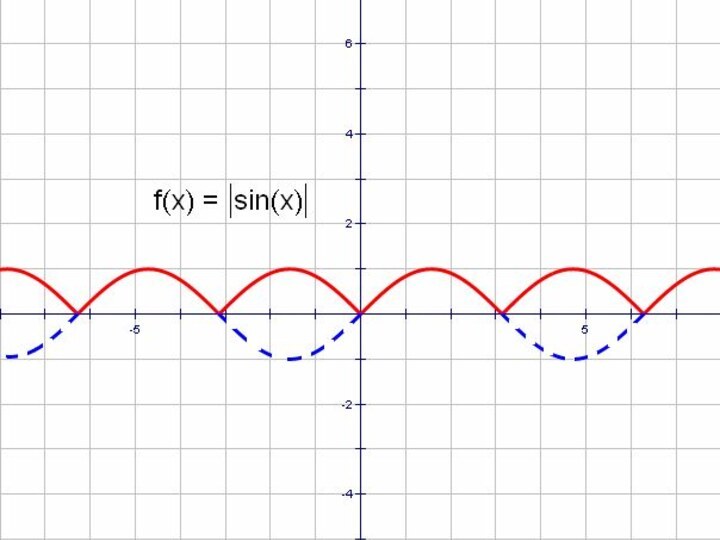
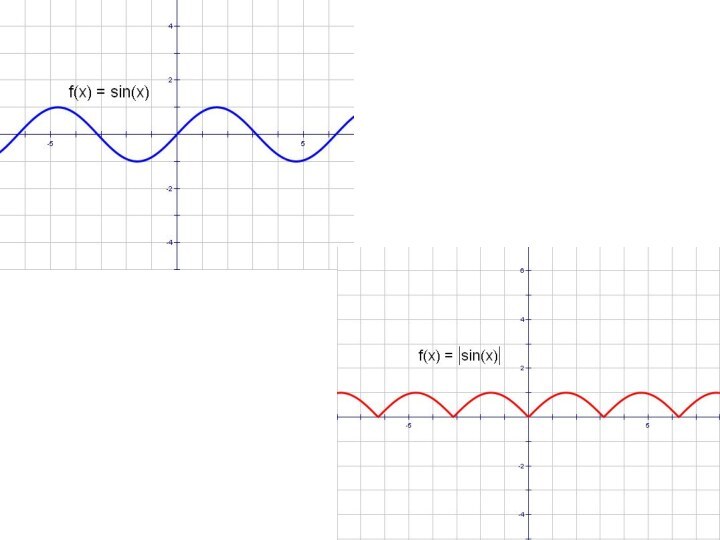
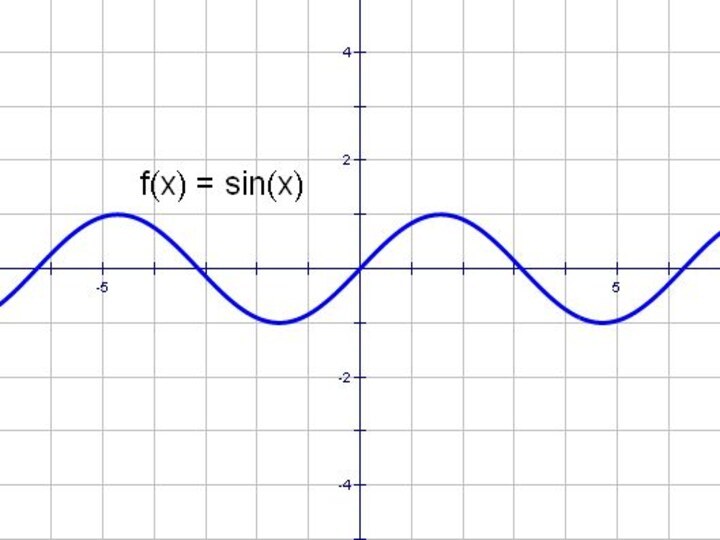
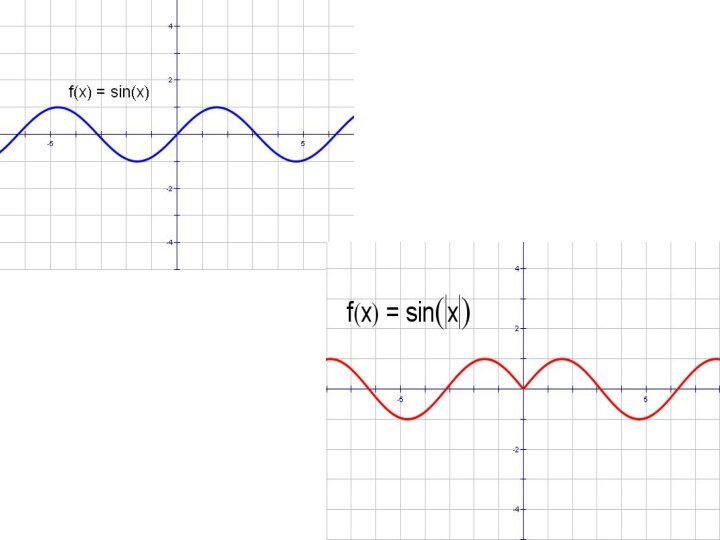
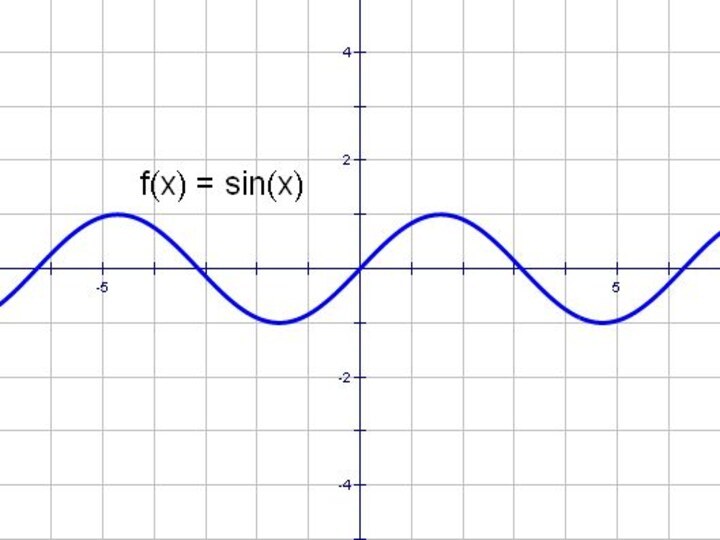
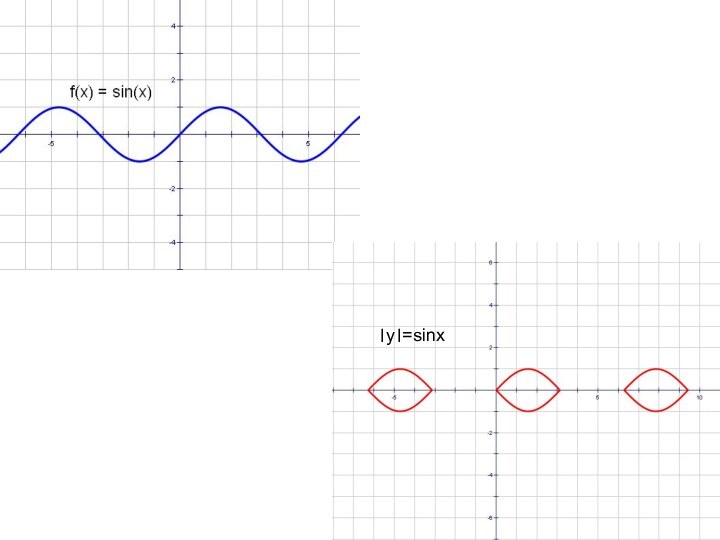
- 32. y = sinx и y = │sin x│
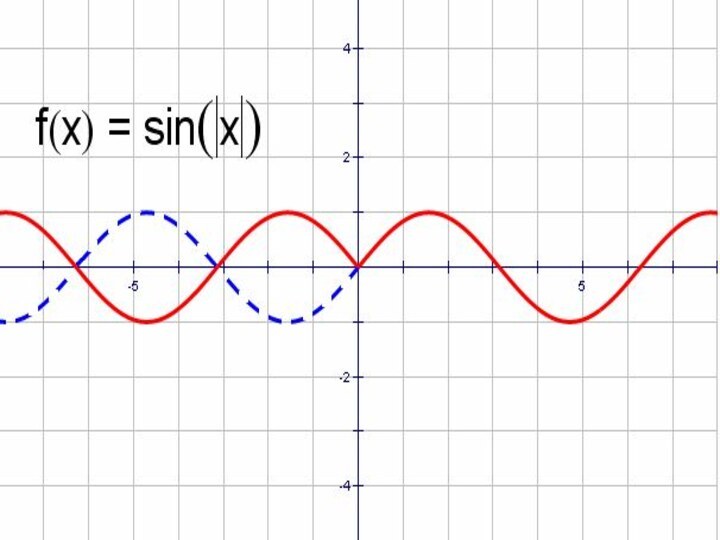
- 36. y = sinx и y = sin│x│
- 40. y = sinx и │y│= sinx
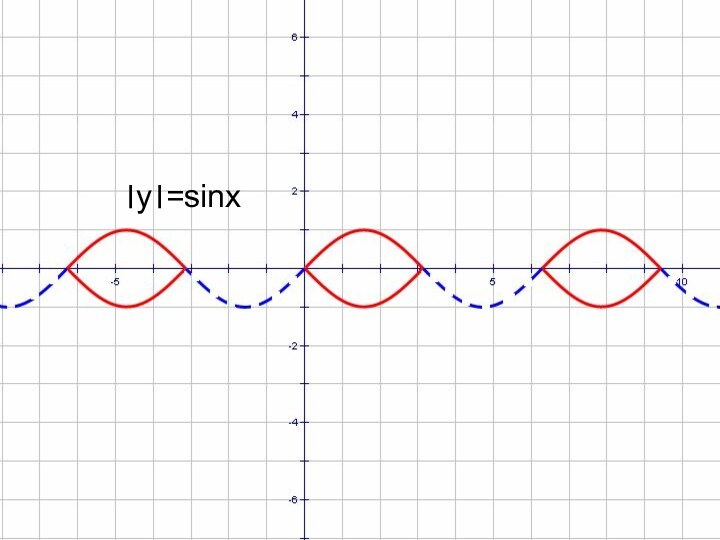
- 42. ।y।=sinx
- 43. ।y।=sinx
- 44. Подведение итогов (обобщение).
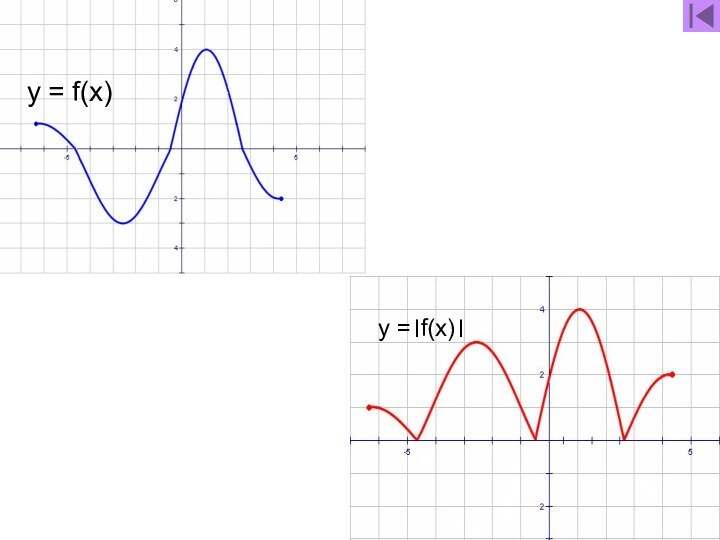
- 45. y = f(x) и y =│f(x)│
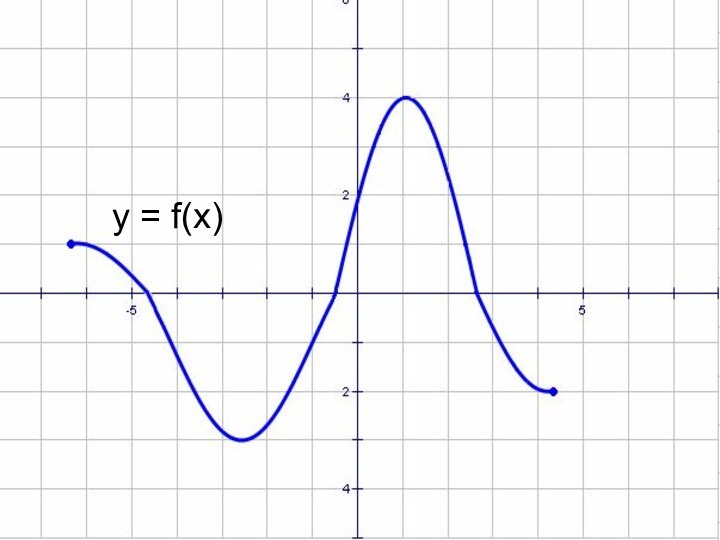
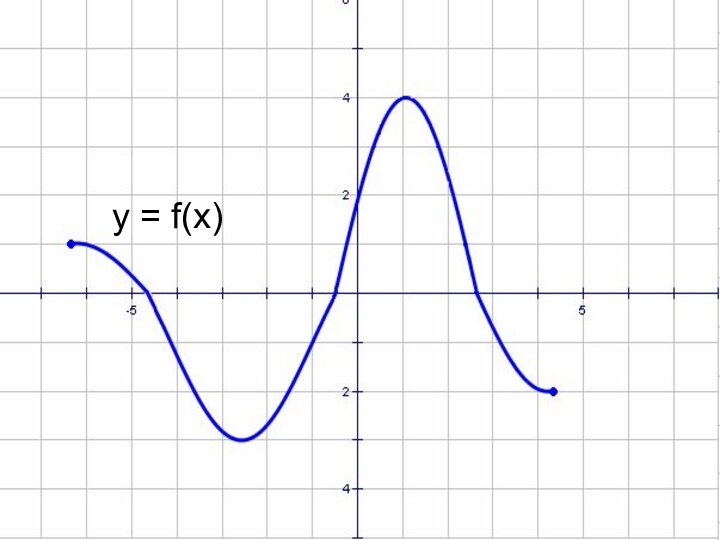
- 46. y = f(x)
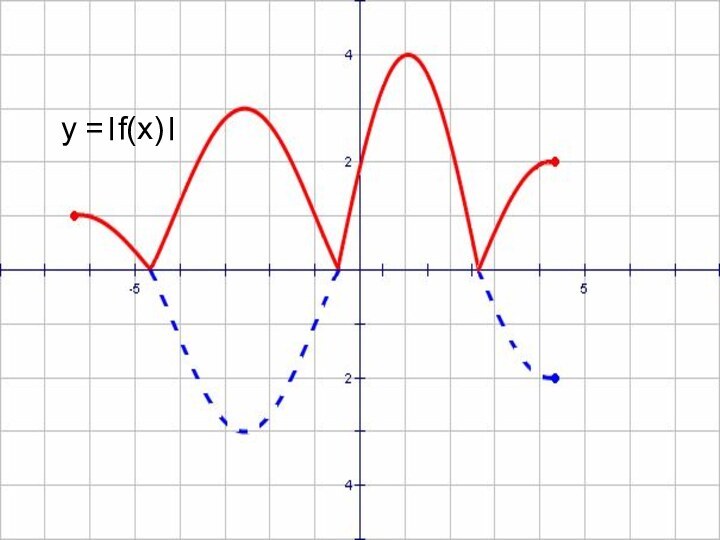
- 47. y =।f(x)।
- 48. y = f(x)y =।f(x)।
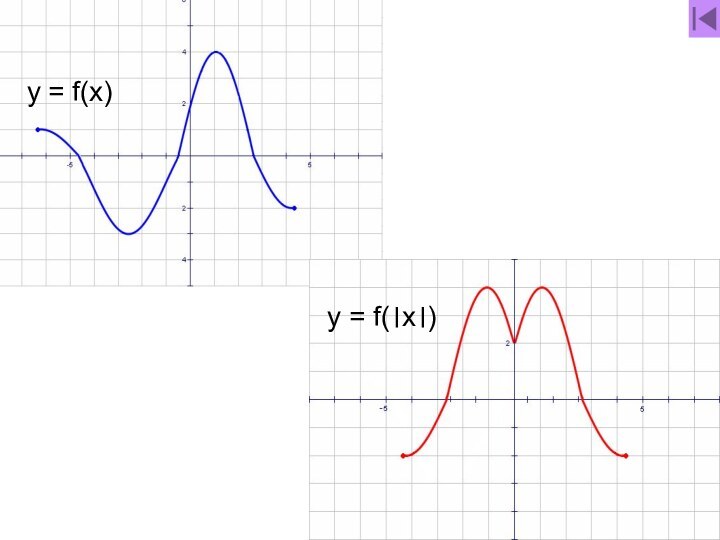
- 49. y = f(x) и y = f(│x│)
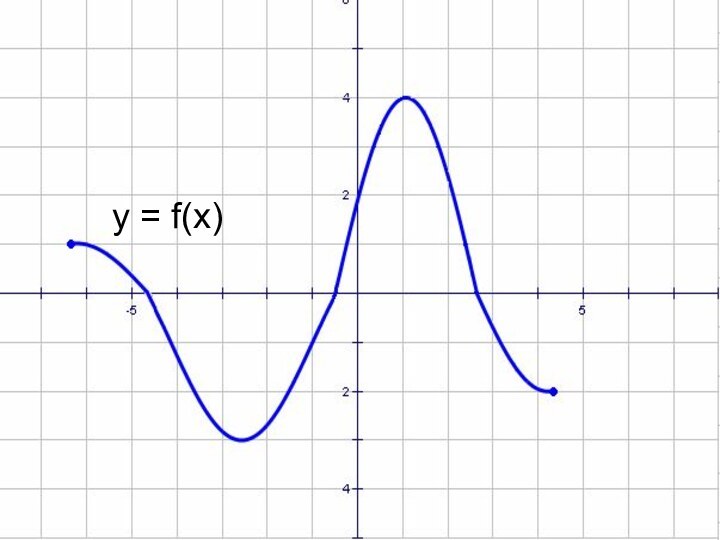
- 50. y = f(x)
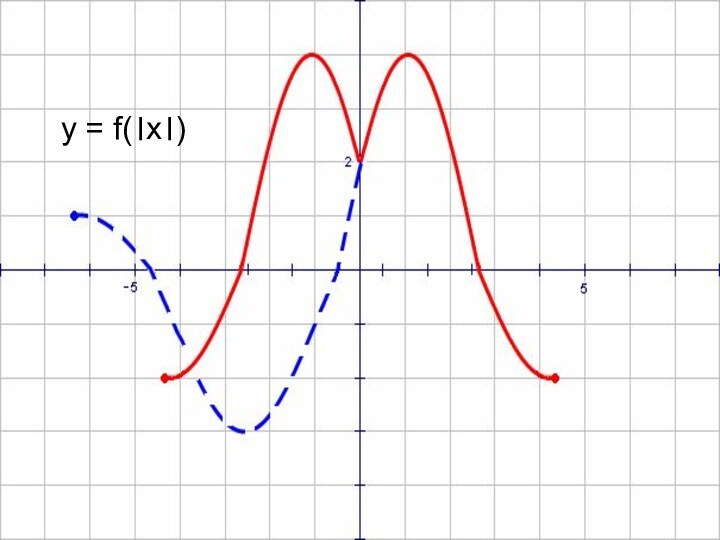
- 51. y = f(।x।)
- 52. y = f(x)y = f(।x।)
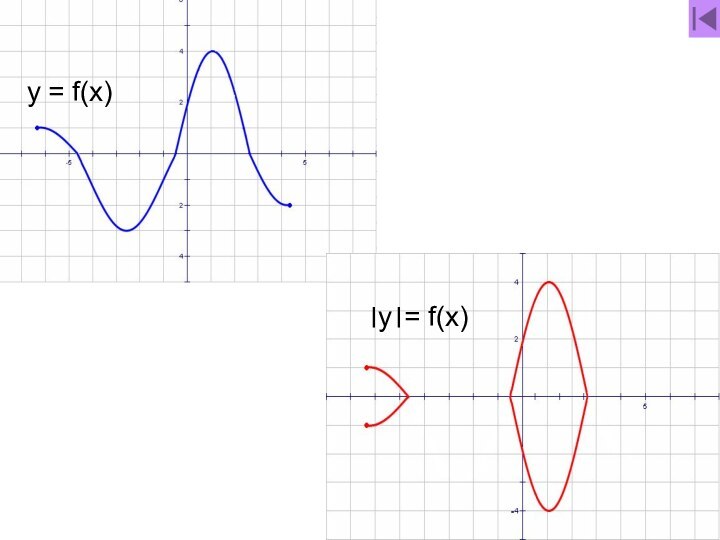
- 53. y = f(x) и │y│= f(x)
- 54. y = f(x)
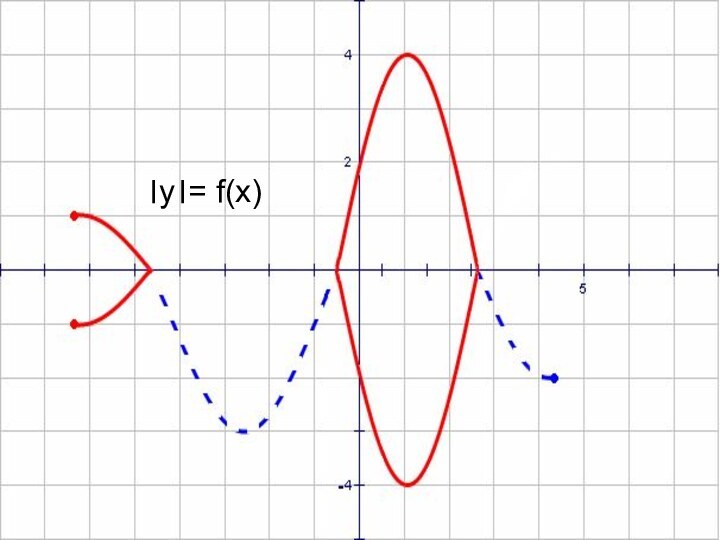
- 55. ।y।= f(x)
- 56. y = f(x)।y।= f(x)
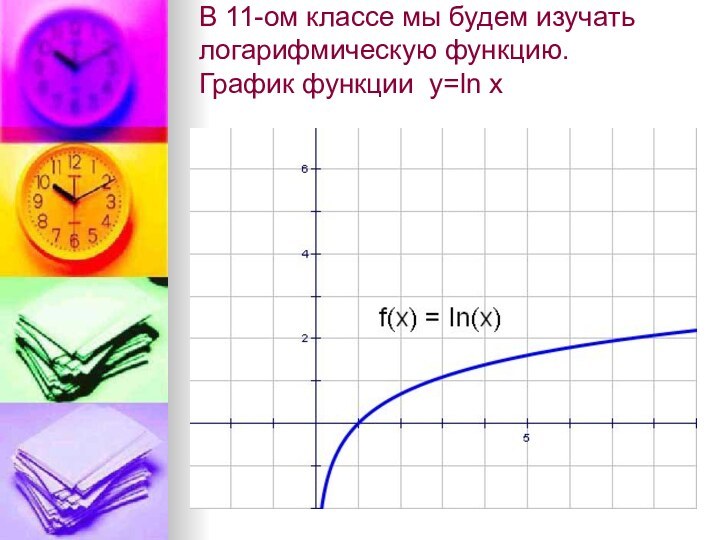
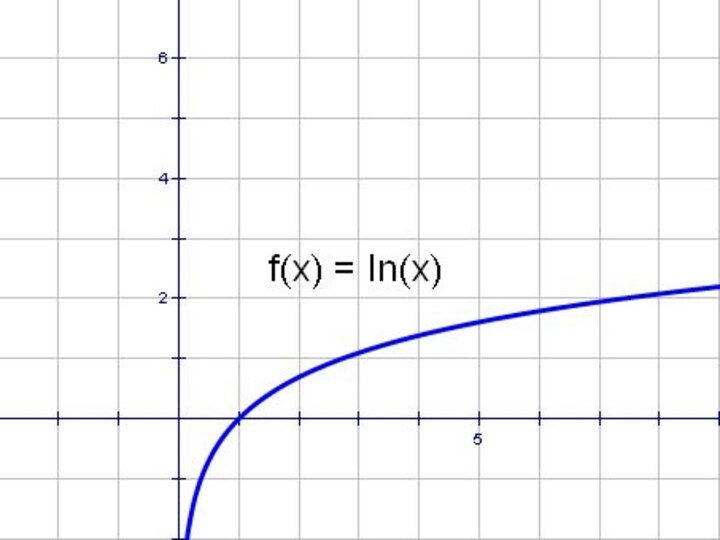
- 57. В 11-ом классе мы будем изучать логарифмическую
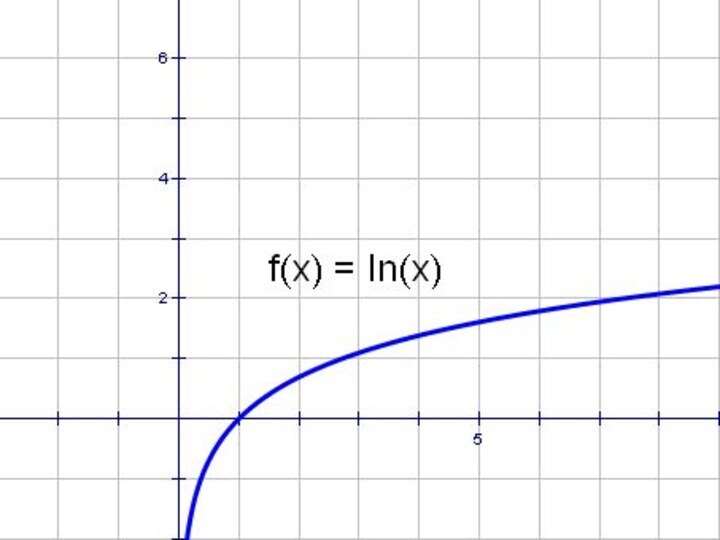
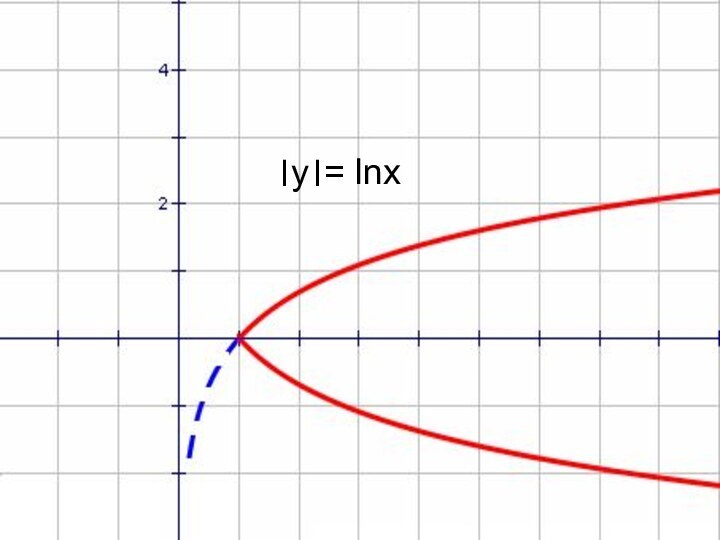
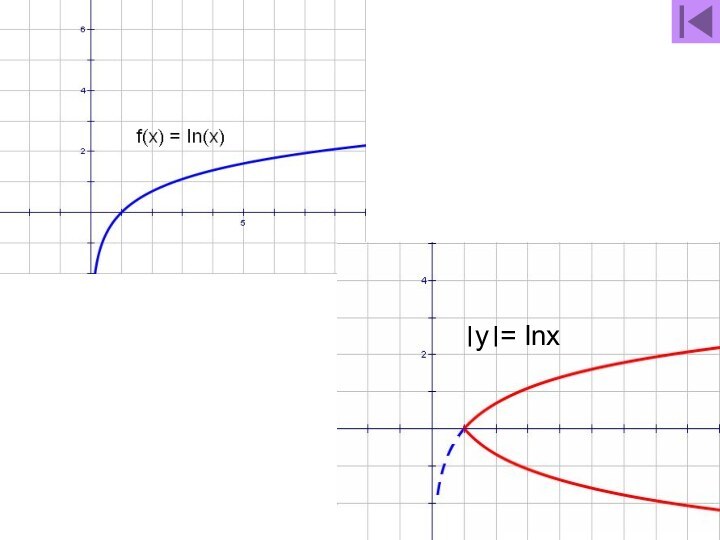
- 58. Попробуйте самостоятельно построить графики: 1.у= |lnx|2. y= ln |x|3. |y|= lnxответыlnx
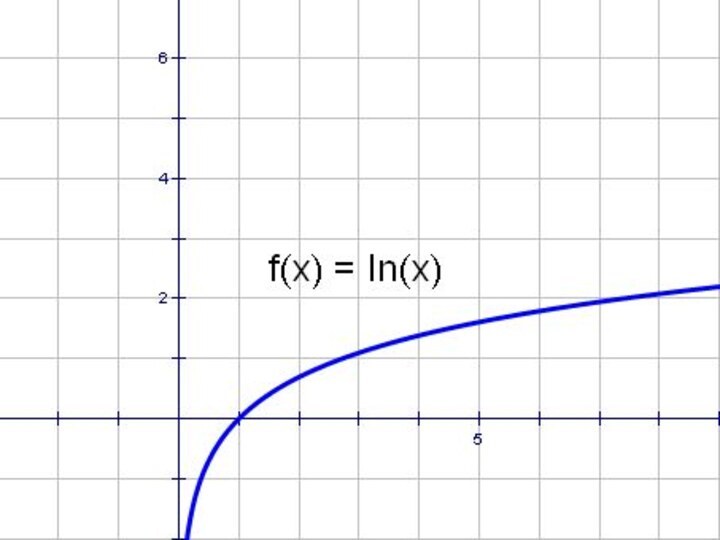
- 59. y = lnx и y =│lnx│
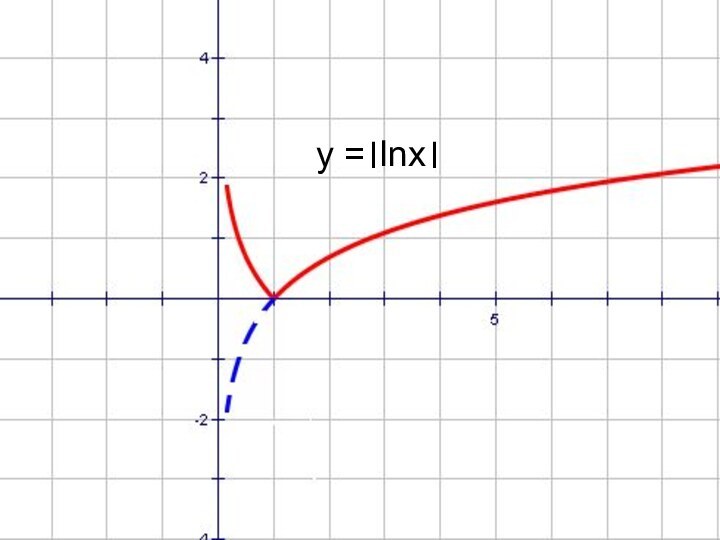
- 61. y =।lnx।
- 62. y =।lnx।
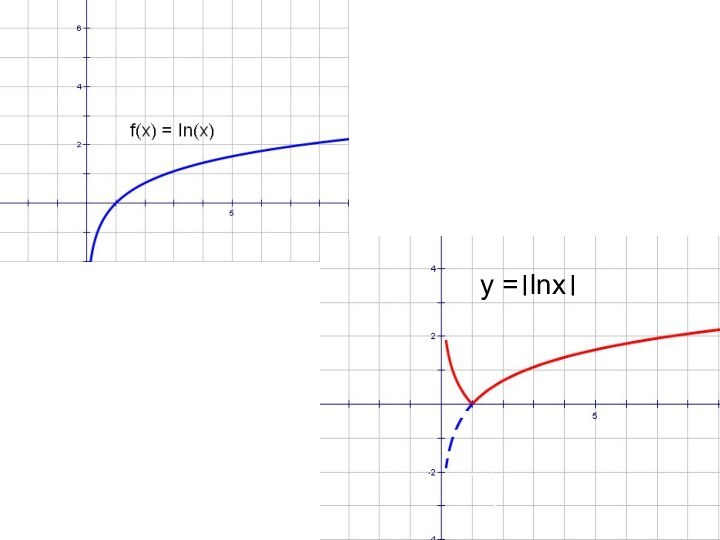
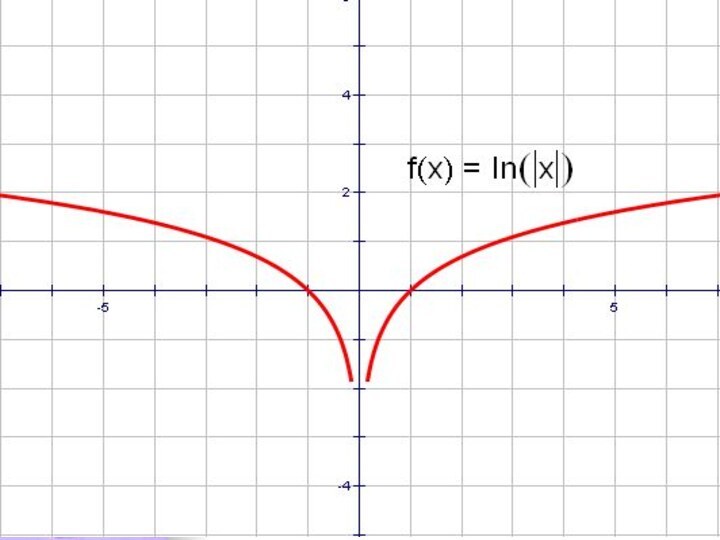
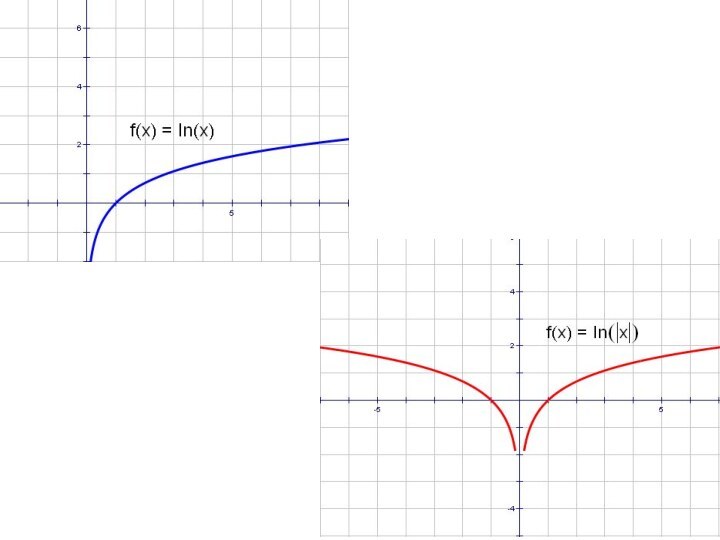
- 63. y = lnx и y = ln│x│
- 67. y = lnx и │y│= lnx
- 69. ।y।= lnx
- 70. ।y।= logx ।y।= lnx
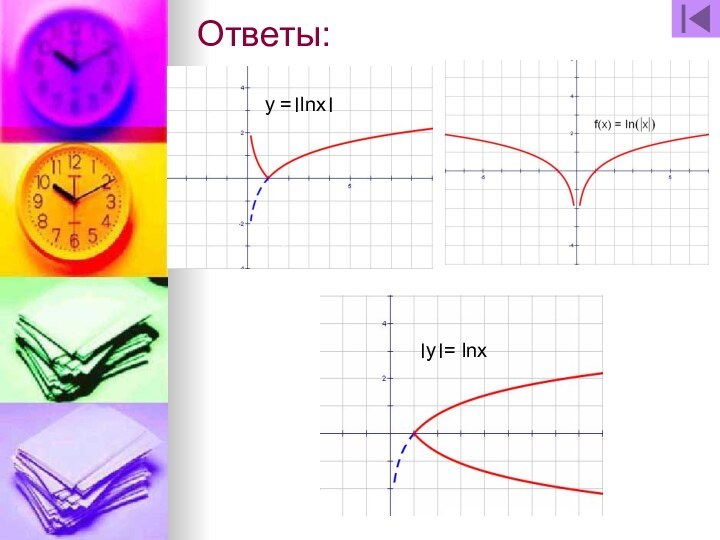
- 71. Ответы:।y।= lnxy =।lnx।
- 72. Домашнее задание:Для функций y = x-2; y
- 73. Что сделали:Закрепили знания на ранее изученных функциях;Перенесли эти знания на новую функцию.
- 74. Скачать презентацию
- 75. Похожие презентации
Тема урока: «Построение графиков функций и уравнений, содержащих переменную под знаком модуля»
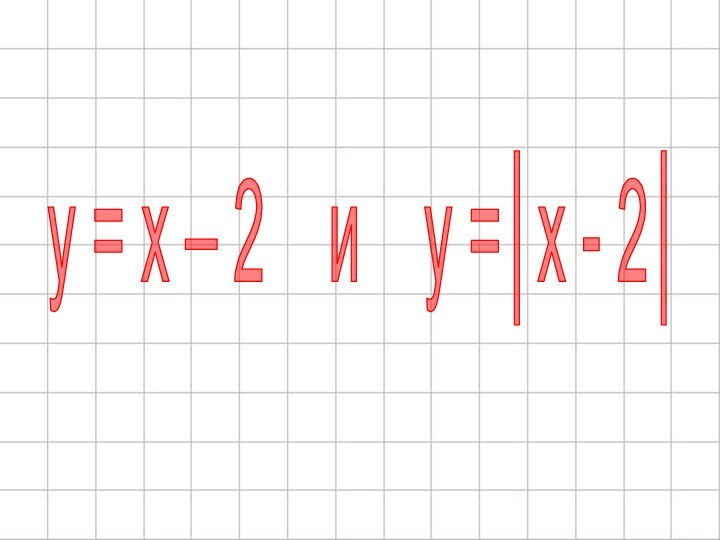
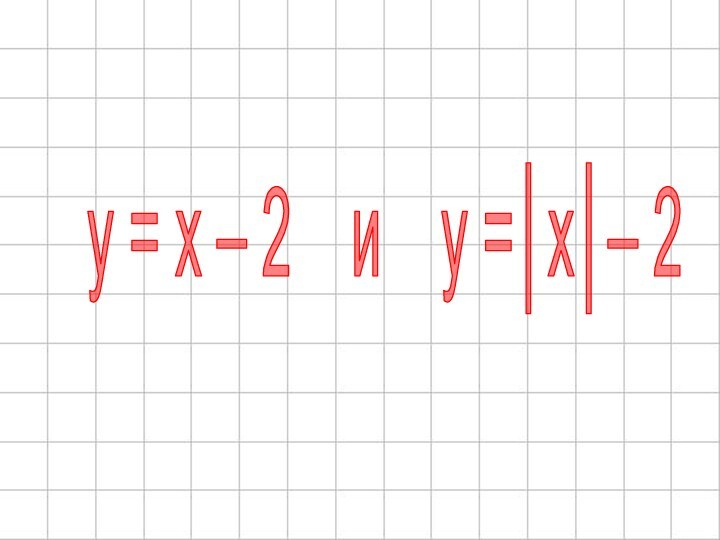
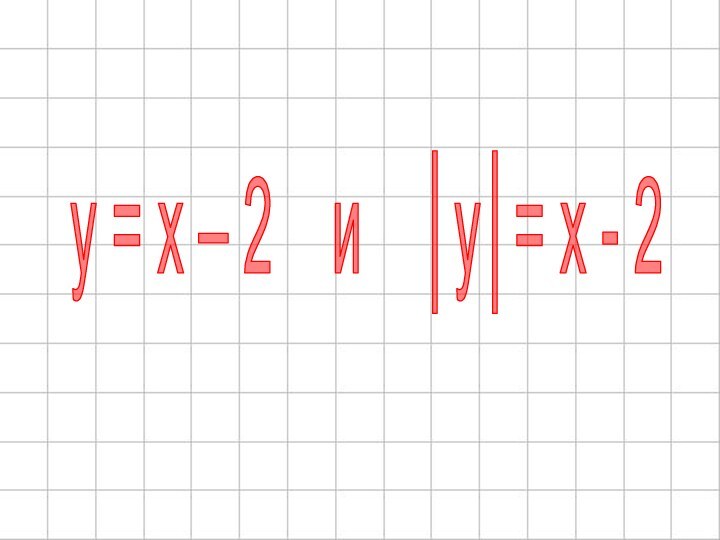
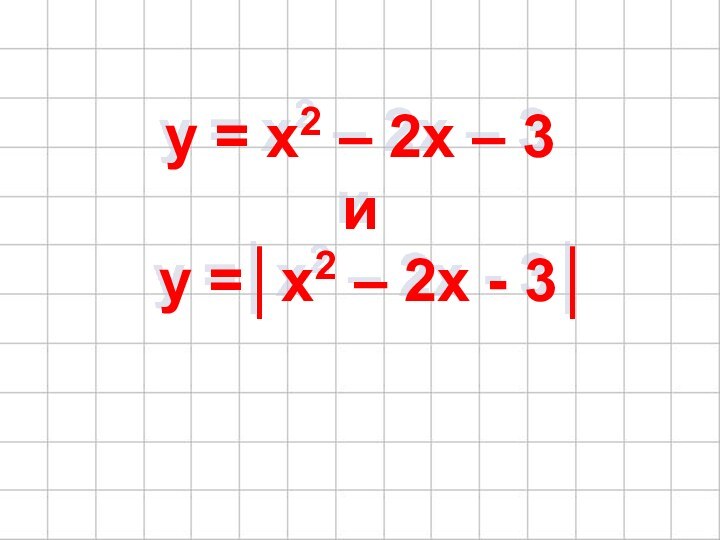
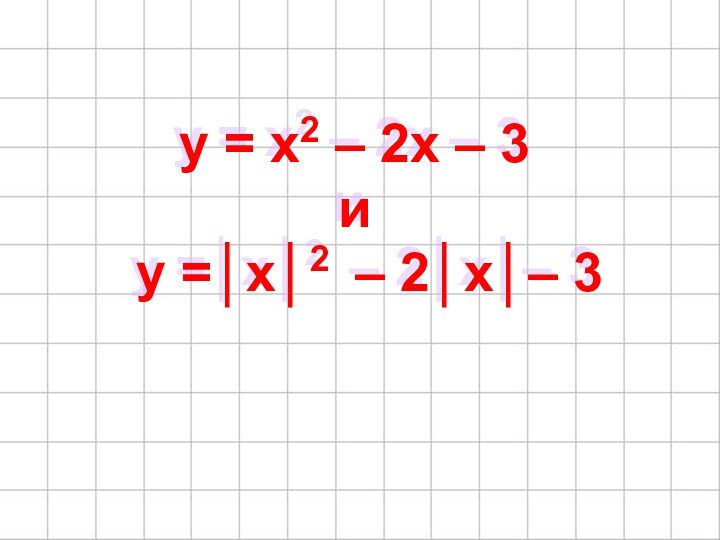
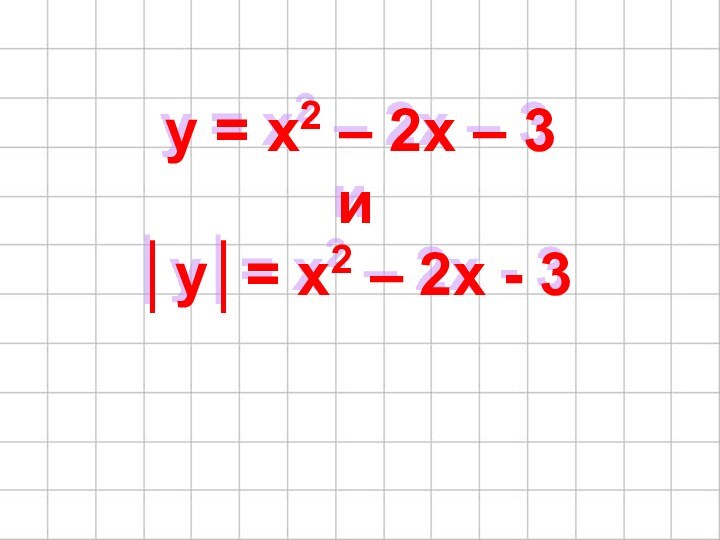
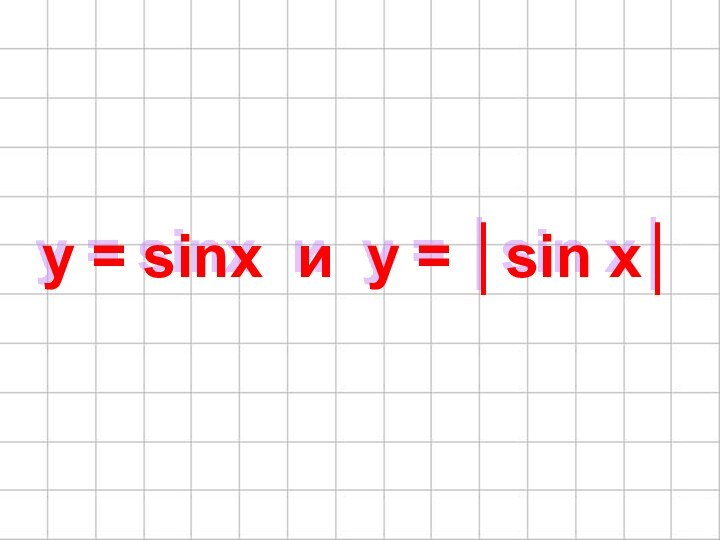
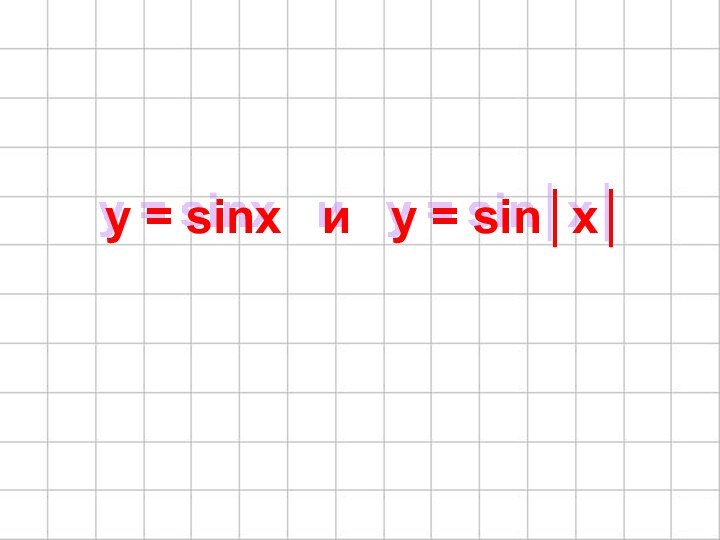
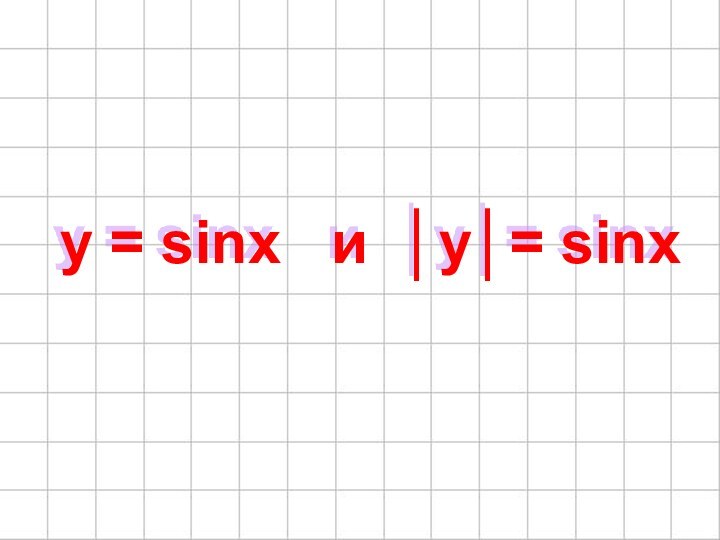
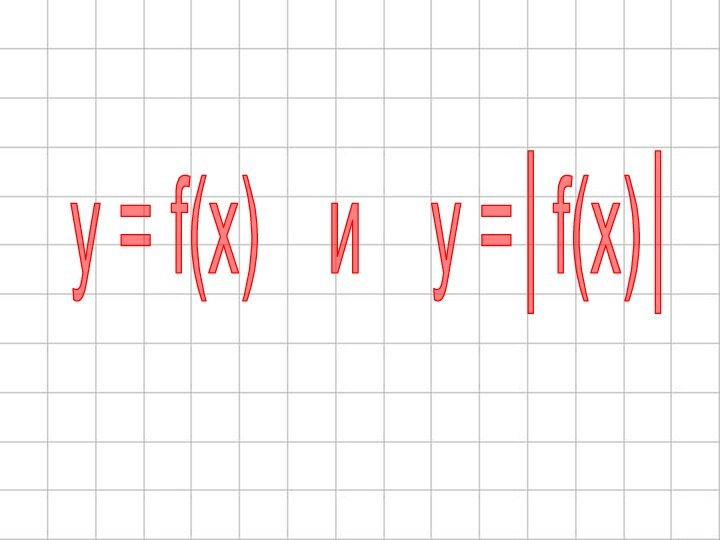
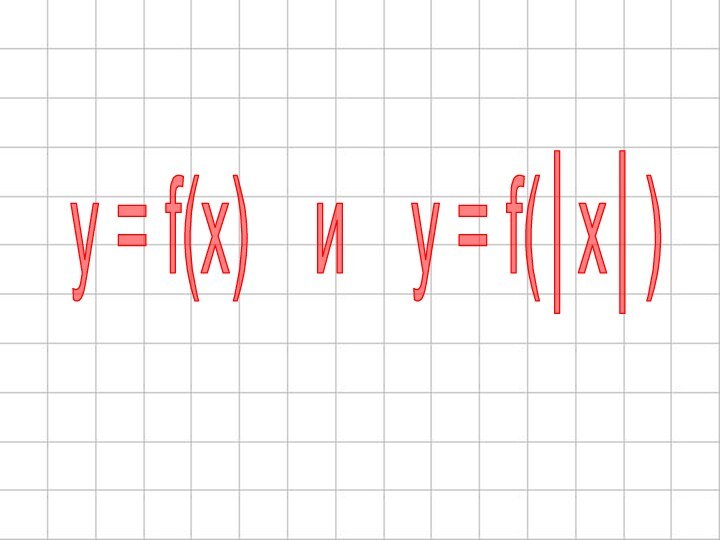
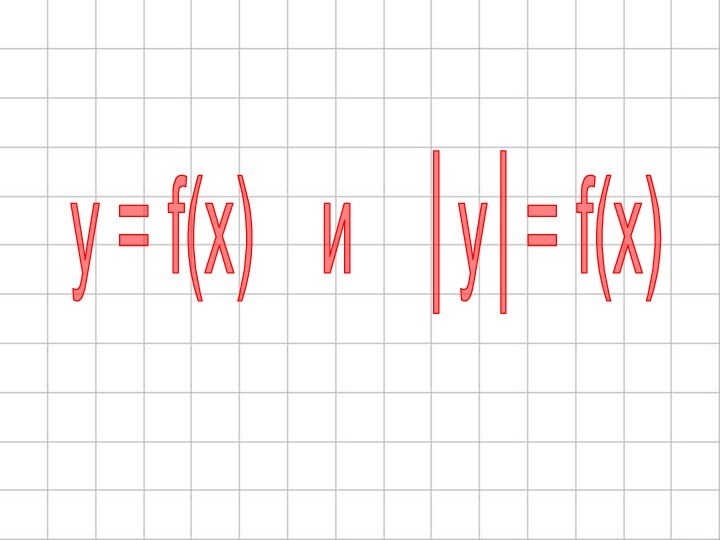
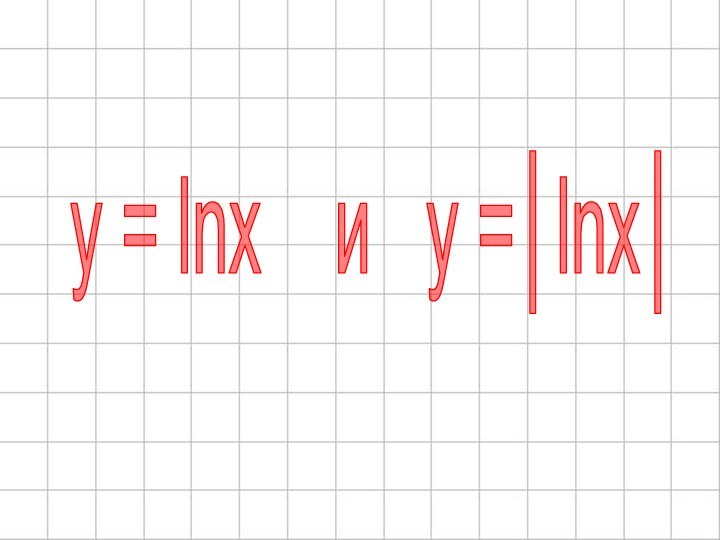
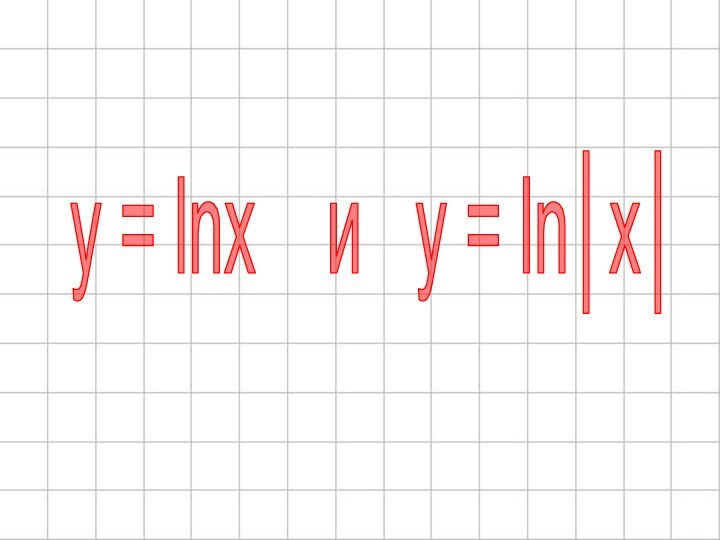
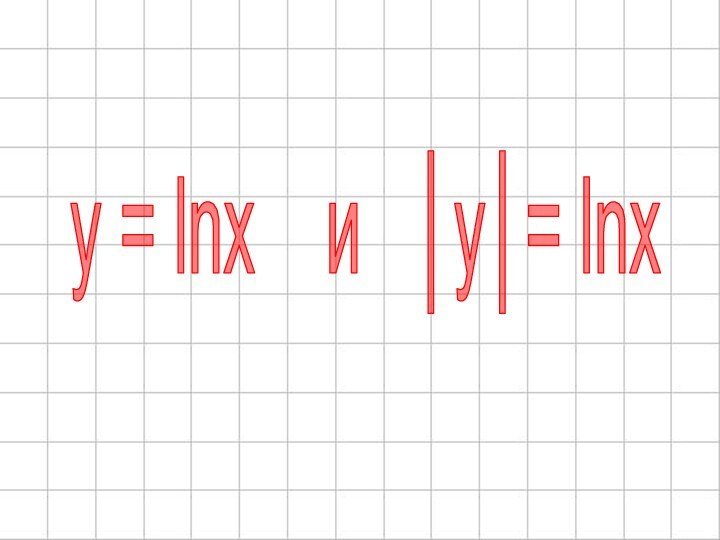
Слайд 2 Тема урока: «Построение графиков функций и уравнений, содержащих переменную
под знаком модуля»
Слайд 5
Задачи:
актуализация знаний о графиках функций и уравнений,
закрепление знаний о построении графиков линейной, квадратичной
и тригонометрической функций, повторение преобразования симметрии относительно прямой;
знакомство с графиком логарифмической функции;
укрепление умений и навыков в работе по образцу и в сходных условиях;
перенос знаний в новые условия.
Слайд 6
Основная цель урока
чтобы учащиеся самостоятельно
овладели новыми знаниями, с помощью наводящих вопросов учителя
переносили усвоенные знания в новые условия, творчески применяли их.
Слайд 7
Рефлексия
Линейная функция
Тригонометрическая
функция
Квадратичная функция
У=f(|x|)
|У|=f(x)
У=|f(x)|
Задание классу
вопрос классу
Домашнее задание
Слайд 72
Домашнее задание:
Для функций
y = x-2;
y =
х2-2x-3;
y = sinx
Продумать построение графиков у = |f(|x|)|
|у| = |f(|x|)|
Слайд 73
Что сделали:
Закрепили знания на ранее изученных функциях;
Перенесли эти
