уметь определять значения синуса, косинуса,
тангенса и котангенса для
точек числовой окружности;
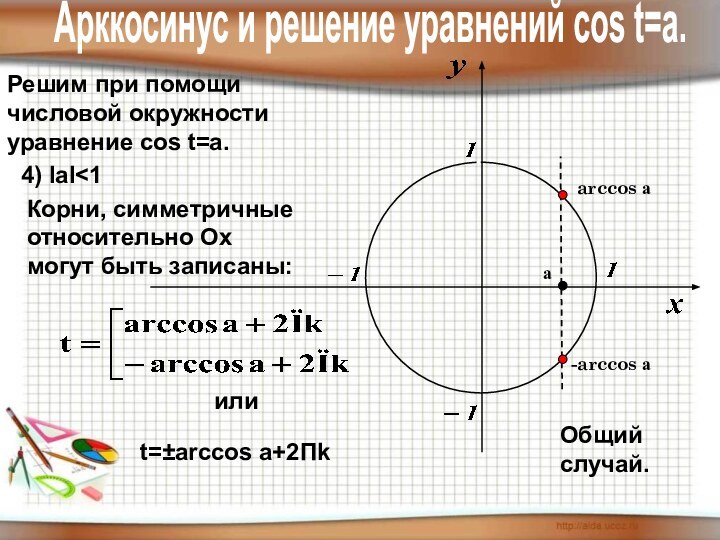
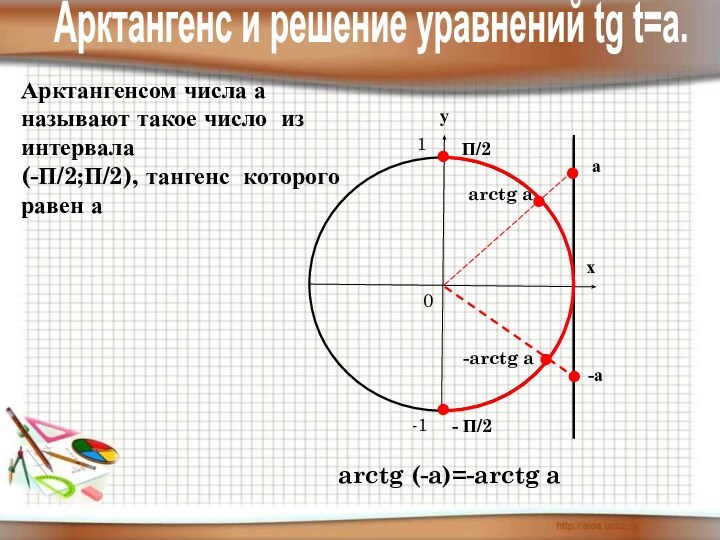
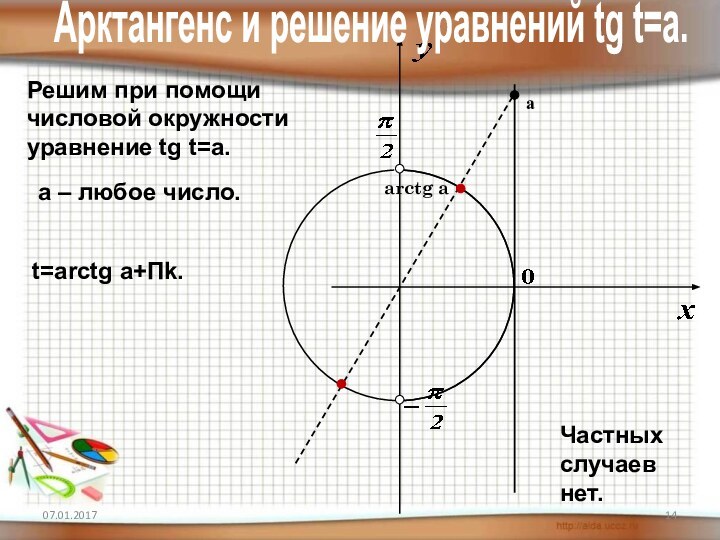
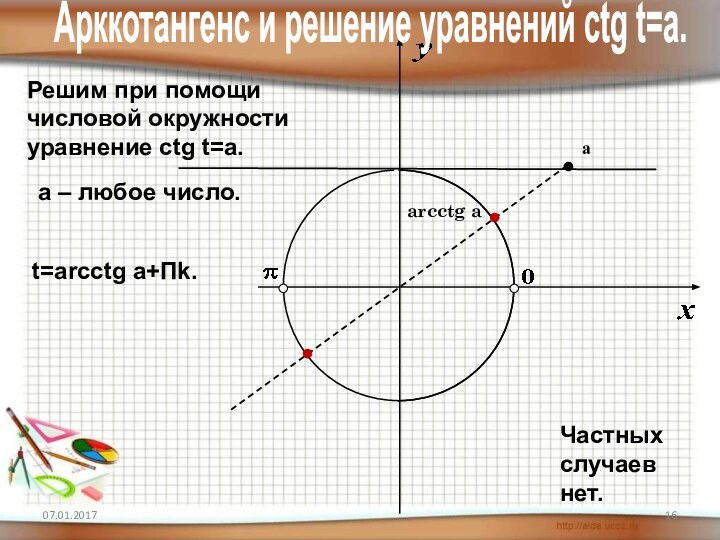
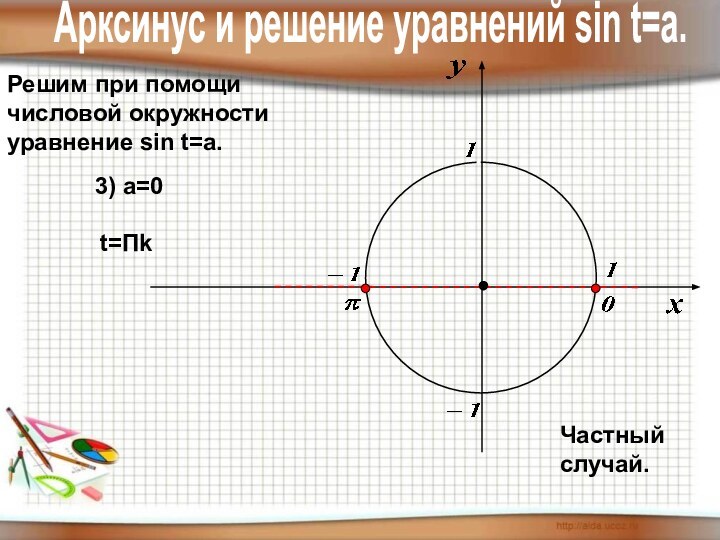
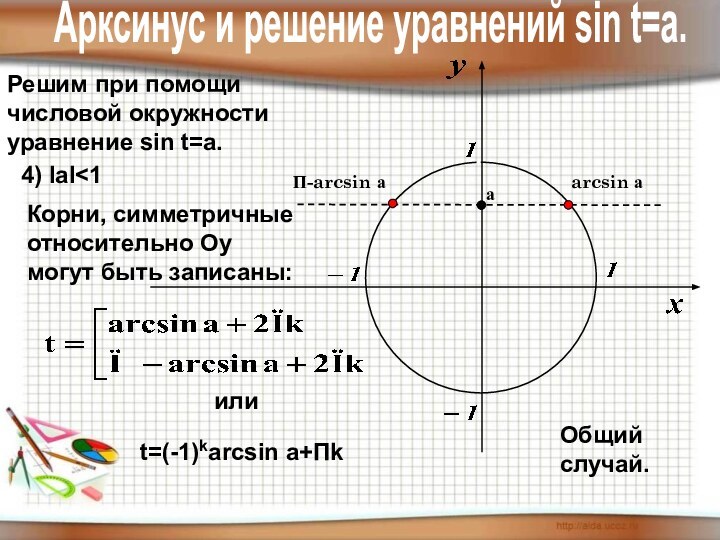
4) знать понятие арксинуса, арккосинуса,
арктангенса, арккотангенса и уметь отмечать их
на числовой окружности.
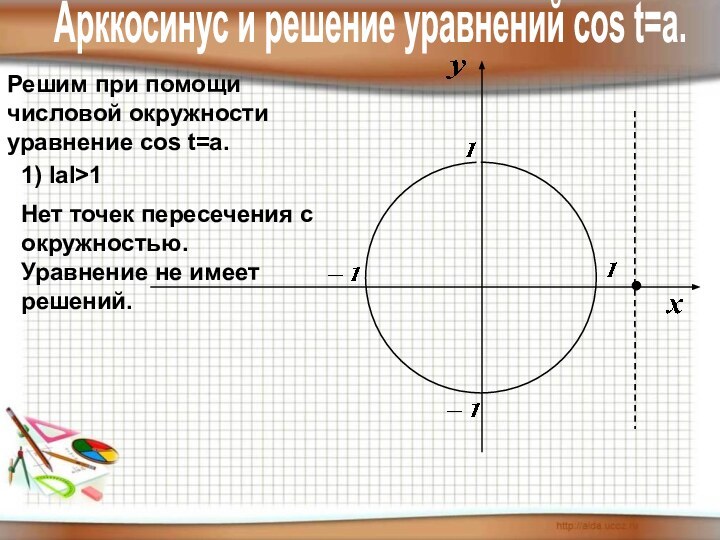
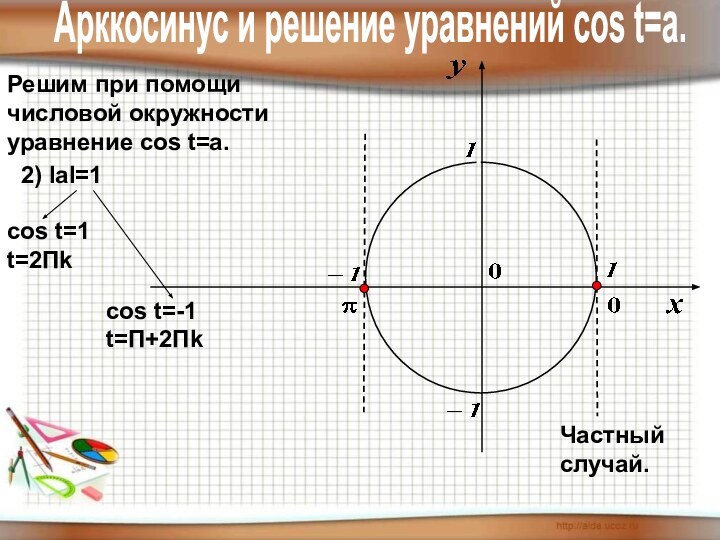
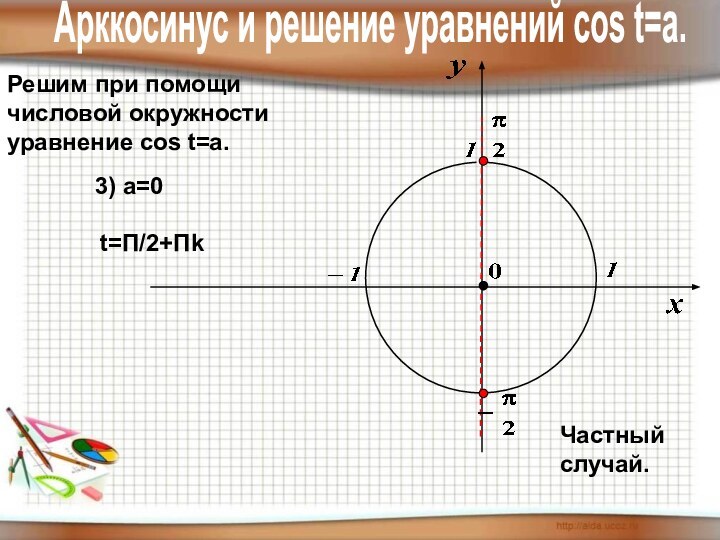
1) уметь отмечать точки на числовой
окружности;
3) знать свойства основных
тригонометрических функций;


![Решение простейших тригонометрических уравнений Арксинусом числа а называют такое число из отрезка [- П/2; П/2], синус](/img/tmb/13/1250175/3a85e807fc99939db6b7a981271a92b4-720x.jpg)


![Решение простейших тригонометрических уравнений П0arccos аАрккосинусом числа а называют такое число из промежутка [0;П ], косинус](/img/tmb/13/1250175/1ff984d4a47486b644cef9013b8defed-720x.jpg)