- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Построение графиков тригонометрических функций
Содержание
- 2. формирование
- 3. Закрепить применение программы MS Excel для построения
- 4. Задание:Постройте в одной координатной плоскости графики функций
- 5. Построение графика функции у = sinx + m 111
- 6. Параллельный перенос графика вдоль оси ОуГрафик функции
- 7. Построение графика функцииy= sin(x+t)222
- 8. Параллельный перенос графика вдоль оси Ох
- 9. xy-11-2y1 = sinx;
- 10. xy-11-2y1 = sinx;
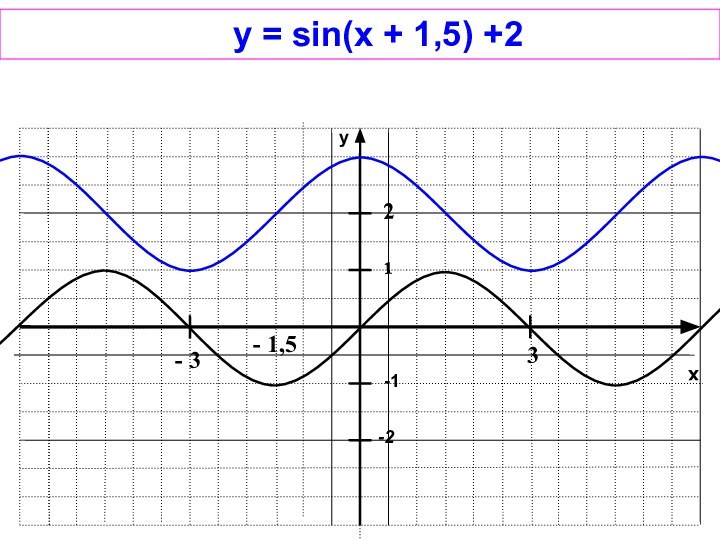
- 11. xy-11-2y = sin(x + 1,5) +2 2 - 3 3- 1,5
- 12. Построение графика функции у = asinx,
- 13. Построение графика функции у=аf(x) График функции у=аf(x)
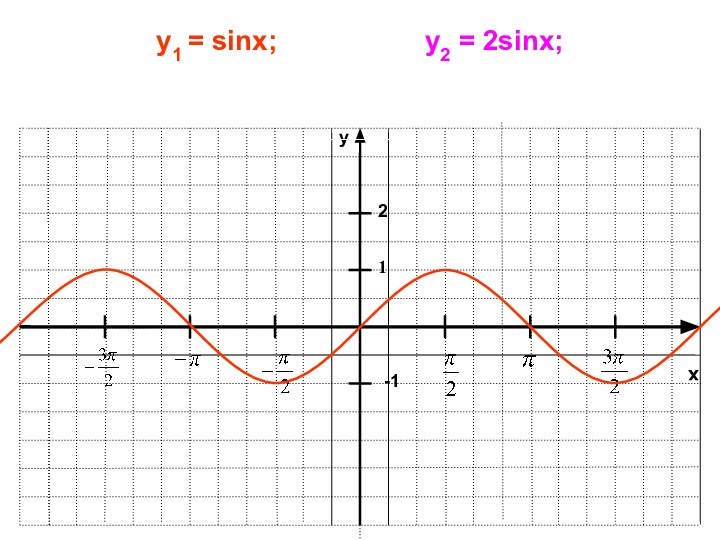
- 14. xy-11y1 = sinx;
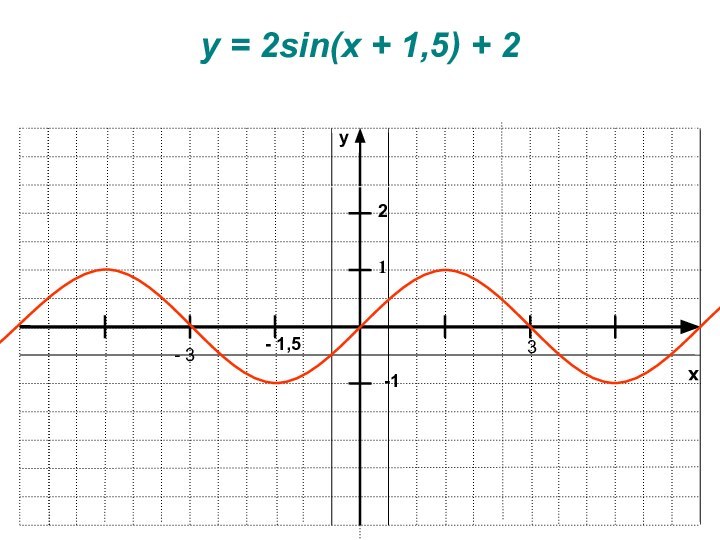
- 15. xy-11y = 2sin(x + 1,5) + 2
- 16. Постройте самостоятельно графики функций: Вариант
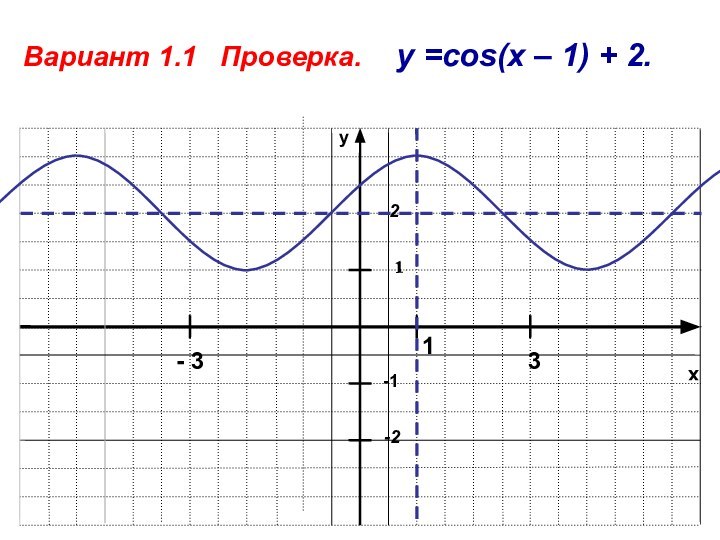
- 17. xy-11-2Вариант 1.1 Проверка. у =cos(x – 1) + 2.2- 3 3 1
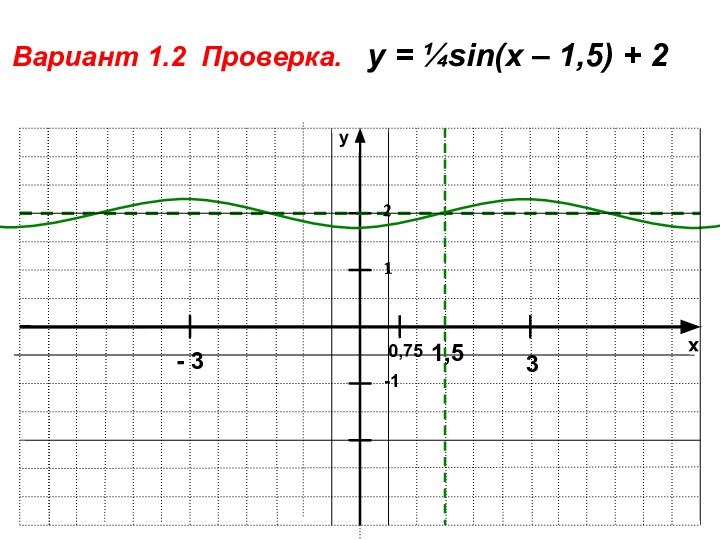
- 18. xy-11Вариант 1.2 Проверка. у = ¼sin(x – 1,5) + 221,5 3- 30,75
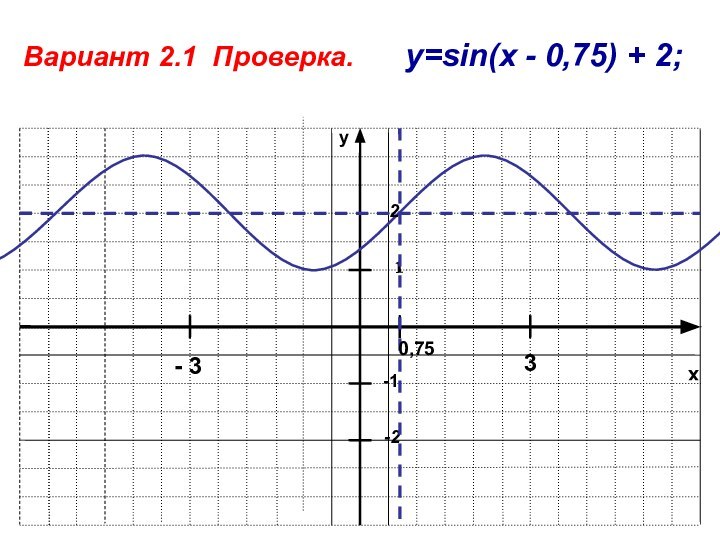
- 19. xy-11-2Вариант 2.1 Проверка. y=sin(x - 0,75) + 2;2- 3 30,75
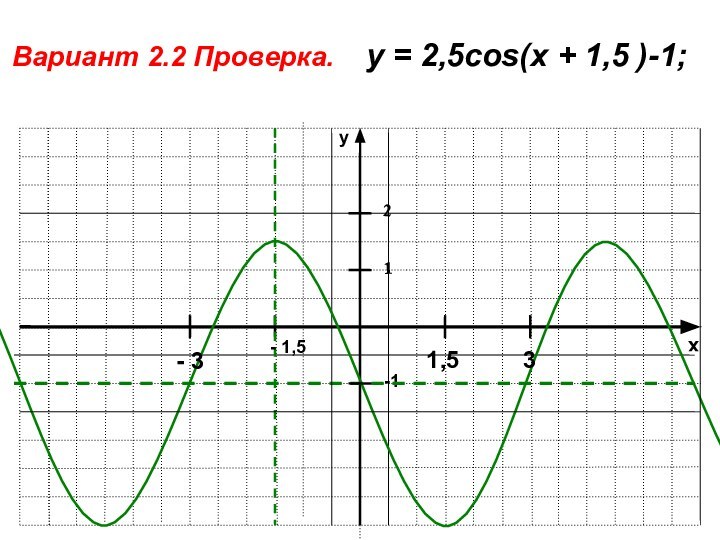
- 20. xy-11Вариант 2.2 Проверка. у = 2,5cos(x + 1,5 )-1; 2- 3 31,5- 1,5
- 21. Вывод: График функции y=f(x + t) +
- 22. Скачать презентацию
- 23. Похожие презентации
формирование знаний и умений преобразовать графики тригонометрических функций. Цель:



![Построение графиков тригонометрических функций Задание:Постройте в одной координатной плоскости графики функций на [-3,6; 3,6] с шагом](/img/tmb/13/1263053/6540fc49b244a0af991a108fa203478c-720x.jpg)








Слайд 3 Закрепить применение программы MS Excel для построения графиков
функций;
Задачи:
Закрепить преобразование графиков тригонометрических функций;
Развитие умения использовать компьютер при
изучении математики.
Слайд 4
Задание:
Постройте в одной координатной плоскости графики функций на
[-3,6; 3,6] с шагом 0,2:
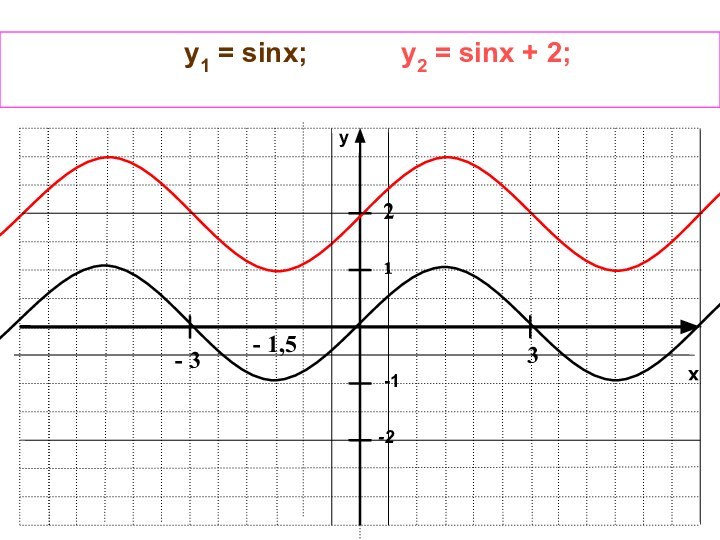
y1 = sinx;
у2 = sinx
+ 2;у3 = sinx - 2.
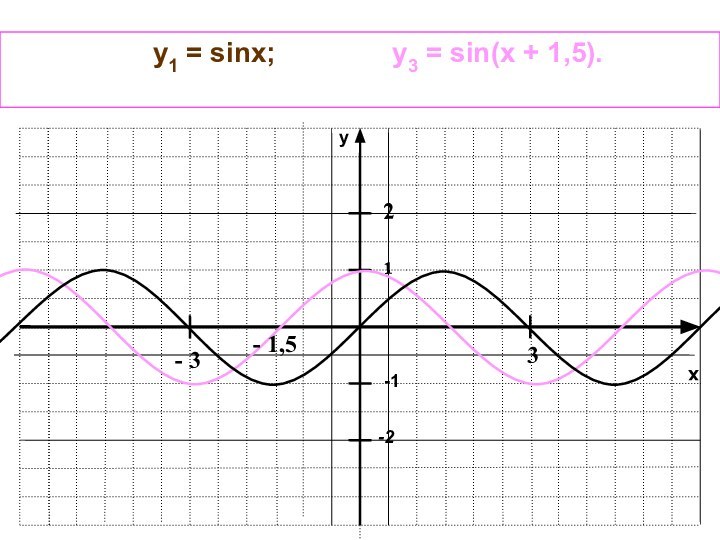
y1 = sinx;
у2 = sin(x + 1,5);
у3 = sin(x – 4,5).
y1 = sinx;
у2 = 2sinx
у3 = ¼ sinx
Слайд 6
Параллельный перенос графика вдоль оси Оу
График функции y=f(x)+m
получается параллельным переносом графика функции y=f(x), вверх на m
единиц, если m>0,или вниз, если m<0.
Слайд 8
Параллельный перенос графика вдоль оси Ох
График функции y
= f(x + t) получается параллельным переносом графика функции
y=f(x) по оси х на |t| единиц масштаба влево, если t > 0и вправо, если t < 0.
Слайд 13
Построение графика функции у=аf(x)
График функции у=аf(x) получаем
растяжением графика функции у=f(x) с коэффициентом а от оси
Ох,если а>1 и сжатием к оси Ох с коэффициентом 0< а <1.
Слайд 16
Постройте самостоятельно графики функций:
Вариант 1.
Вариант 2.
1. у = cos(x – 1 ) + 2; 1. y=sin(x – 0,75) + 2;
2. у = ¼sin(x – 1,5 ) + 2; 2. y=2,5cos(x + 1,5) - 1;
Слайд 21
Вывод:
График функции y=f(x + t) + m
может быть получен из графика функции y=f(x) с помощью
двух последовательных сдвиговна t единиц вдоль оси Ох и на m единиц вдоль оси Оу.