- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теория игр. Решение задач в смешанных стратегиях
Содержание
- 2. ПЛАН ЛЕКЦИИ1) Решение задач в смешанных стратегиях
- 3. ТЕОРИЯ ИГР – это раздел математики, изучающий
- 4. Пусть в игре участвуют два игрока А
- 5. Игру можно представить в виде матрицыСтолбцы –
- 6. Выигрыш зависит от СТРАТЕГИИ, последовательности действий игрока в конкретной ситуации.ОПТИМАЛЬНАЯ СТРАТЕГИЯ ИГРОКАМАКСИМАЛЬНЫЙ ВЫИГРЫШ
- 7. РЕШИМ ЗАДАЧУ:Два игрока, не глядя друг на
- 8. Принцип МАКСИМИНА – выбрать ту стратегию, чтобы
- 9. СМЕШАННЫЕ СТРАТЕГИИЕсли в игре нет седловой точки,
- 10. 1) Теорема и максимине. В конечной игре
- 11. 2) Основная теорема матричных игр. Любая матричная
- 12. Те из чистых стратегий игроков А и
- 13. 1. Решение задач в смешанных стратегиях размерностью 2х2Аналитический методГрафический метод
- 14. р1р2q1 q2 Аналитический метод
- 15. Если игрок А использует свою оптимальную смешанную
- 16. ЗАДАНИЕ:Найти, чему равны p1, p2, v, если:a11p1 + a21p2 = va12p1 + a22p2 = v
- 17. =Получаем решение матричной игры:
- 18. Вычислив оптимальное значение V, можно вычислить и
- 19. ПримерПлатежная матрица имеет следующий вид:Найти решение игры аналитическим методом
- 20. Решение:Сначала необходимо определить, решается ли данная игра
- 21. Обозначим: р1=р, то р2=1-р
- 22. 3p+7(1-p)=V8p+4(1-p)=V3p+7-7p=8p+4-4p-4p+7=4p+48p=3p1=3/8p2=1-3/8=5/8(3/8;5/8) – вектор вероятностиV=3*3/8+7*5/8=5,5 – среднее значение
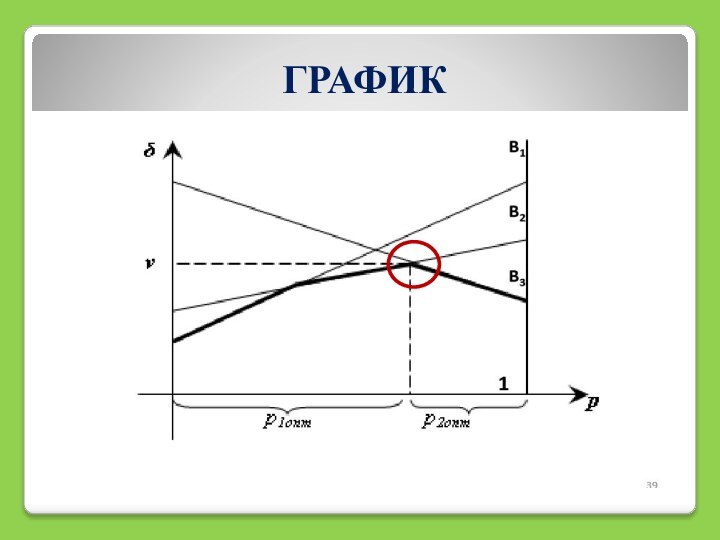
- 23. Графический метод решения 2х2Найдем оптимальную стратегию для
- 24. 2. Найдем оптимальную стратегию для второго игрока
- 25. Пример.Матричная игра 2х2 задана следующей матрицей:Найти решение игры графическим методом
- 26. Решение:Сначала необходимо определить, решается ли данная игра
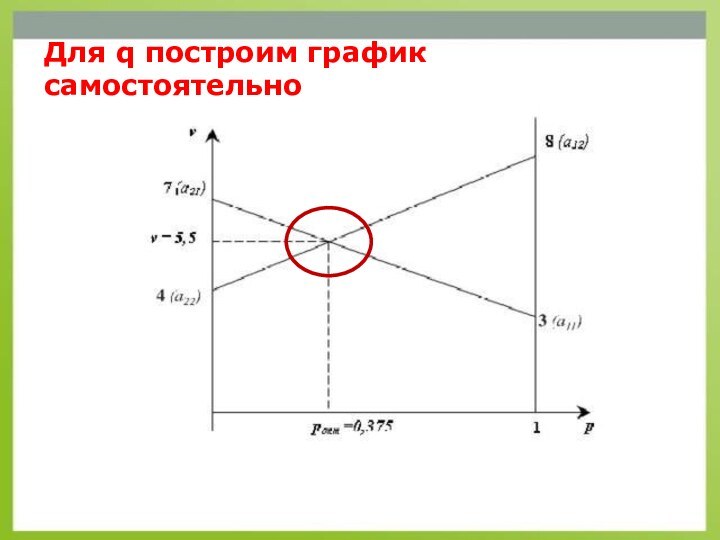
- 27. Для q построим график самостоятельно
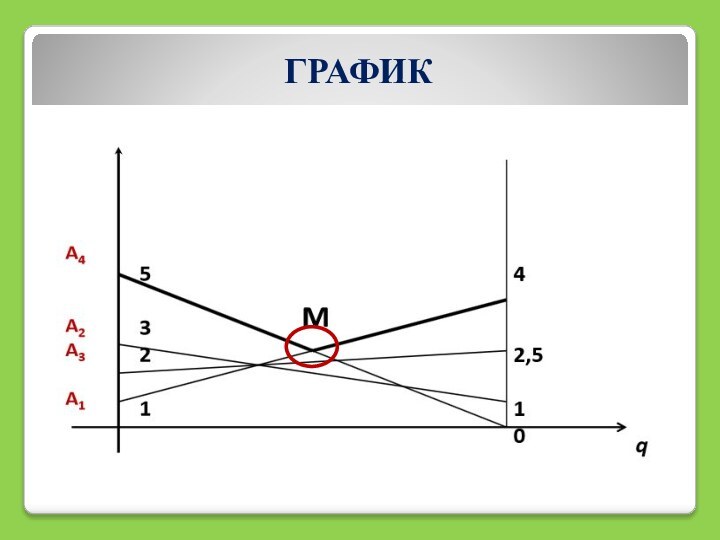
- 28. 2. Решение задач в смешанных стратегиях размерностью 2хn
- 31. ГРАФИК
- 32. ПРИМЕР:
- 36. Используя алгебраический метод решения этой игры, получаем:ОТВЕТ:
- 37. Решение игры mx2 осуществляется аналогично. Но в
- 38. ПРИМЕР:
- 40. ГРАФИК
- 41. ОТВЕТ: оптимальные смешанные стратегии игроков: Sa =
- 42. Скачать презентацию
- 43. Похожие презентации




































Слайд 3 ТЕОРИЯ ИГР – это раздел математики, изучающий математические
модели принятия решений в конфликтных ситуациях.
ИГРА – это упрощенная
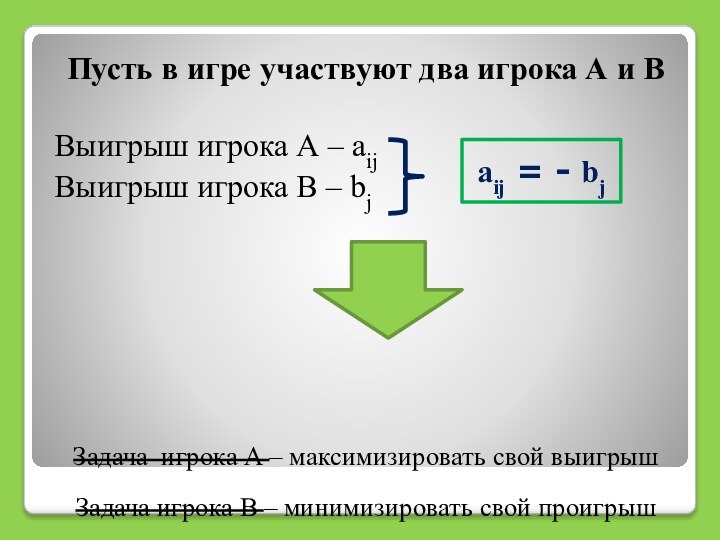
математическая модель конфликтной ситуации, сторонами которой являются ИГРОКИСлайд 4 Пусть в игре участвуют два игрока А и
В
Выигрыш игрока А – aij
Выигрыш игрока B – bj
Задача
игрока А – максимизировать свой выигрышЗадача игрока В – минимизировать свой проигрыш
aij = - bj
Слайд 5
Игру можно представить в виде матрицы
Столбцы – стратегии
игрока В
Строки – стратегии игрока А
Матрица называется ПЛАТЕЖНОЙ МАТРИЦЕЙ,
где элементы этой матрицы это выигрыши игрока А.Слайд 6 Выигрыш зависит от СТРАТЕГИИ, последовательности действий игрока в
конкретной ситуации.
ОПТИМАЛЬНАЯ СТРАТЕГИЯ ИГРОКА
МАКСИМАЛЬНЫЙ ВЫИГРЫШ
Слайд 7
РЕШИМ ЗАДАЧУ:
Два игрока, не глядя друг на друга,
кладут на стол по картонному кружку красного (К), зеленого
(З) или синего (с) цветов.Сравнивают цвета и расплачиваются друг с другом так как показано в матрице игры.
Считая, что игра повторяется многократно, определить оптимальные стратегии каждого игрока.
Вк Вз Вс
Ак -2 2 -1
Аз 2 1 1
Ас 3 -3 1
Слайд 8 Принцип МАКСИМИНА – выбрать ту стратегию, чтобы при
наихудшем поведении противника получить максимальный выигрыш.
Вк Вз ВсАк -2 2 -1
Аз 2 1 1
Ас 3 -3 1
Min выигрыша А
-2
1
-3
Max выигрыша А
Min проигрыша В
3 2 1
α = max -2;1;-3 = 1
- нижняя цена игры
b = min 3; 2; 1 = 1
- верхняя цена игры
α = b = ⱱ = 1 – седловая точка
(Аз;Вс) – пара оптим. стратегий
Слайд 9
СМЕШАННЫЕ СТРАТЕГИИ
Если в игре нет седловой точки, то
можно найти нижнюю и верхнюю цены игры, которые указывают,
что игрок 1 не должен надеяться на выигрыш больший, чем верхняя цена игры, и может быть уверен в получении выигрыша не меньше нижней цены игры.Поиск такого решения приводит к необходимости применять смешанные стратегии, то есть чередовать чистые стратегии с какими-то частотами.
Слайд 10 1) Теорема и максимине. В конечной игре двух
игроков (коалиций) с нулевой суммой (матричной игре) при a
= b имеет место равенство:Теорема о максимине указывает на существование равновесия для случая VA = VB при a = b, и, следовательно, существования оптимальных смешанных стратегий.
Слайд 11
2) Основная теорема матричных игр.
Любая матричная игра
имеет, по крайней мере, одно оптимальное решение, в общем
случае, в смешанных стратегиях и соответствующую цену V.Цена игры V – средний выигрыш, приходящийся на одну партию, - всегда удовлетворяет условию:
т.е. лежит между нижней a и верхней в
ценами игры.
Слайд 12 Те из чистых стратегий игроков А и В,
которые входят в их оптимальные смешанные стратегии с вероятностями,
не равными нулю, называются активными стратегиями.
Слайд 13
1. Решение задач в смешанных стратегиях размерностью 2х2
Аналитический
метод
Графический метод
Слайд 14
р1
р2
q1 q2
Аналитический метод решения
игры 2х2
Оптимальное решение в смешанных стратегиях: SA = |
p1, p2 | и SB = | q1, q2 |Вероятности применения (относительные частоты применения) чистых стратегий удовлетворяют соотношениям:
p1 + p2 = 1
q1 + q2 = 1
Слайд 15 Если игрок А использует свою оптимальную смешанную стратегию,
а игрок В – свою чистую активную стратегию В1,
то цена игры V равна:a11p1 + a21p2 = v
2) Если игрок А использует свою оптимальную смешанную стратегию, а игрок В – свою чистую активную стратегию В2, то цена игры V равна:
a12p1 + a22p2 = v
Слайд 18 Вычислив оптимальное значение V, можно вычислить и оптимальную
смешанную стратегию второго игрока из условия:
a11p1 + a21p2 =
v и a12p1 + a22p2 = v
Слайд 20
Решение:
Сначала необходимо определить, решается ли данная игра в
чистых стратегиях, то есть существует ли седловая точка или
нет.α < β, при этом цена игры V ϵ [4;7]
Игра не имеет седловой точки, следовательно, не решается в чистых стратегиях
=
Слайд 21
Обозначим: р1=р, то р2=1-р
q1=1, то q2=1-q
р
1-р
q
1-q3p+7(1-p)=V
8p+4(1-p)=V
3q+8(1-q)=V
7q+4(1-q)=V
Слайд 22
3p+7(1-p)=V
8p+4(1-p)=V
3p+7-7p=8p+4-4p
-4p+7=4p+4
8p=3
p1=3/8
p2=1-3/8=5/8
(3/8;5/8) – вектор вероятности
V=3*3/8+7*5/8=5,5 – среднее значение выигрыша
А
3q+8(1-q)=V
7q+4(1-q)=V
3q+8-8q=7q+4-4q
-5q+8=3q+4
q1=1/2, q2=1/2; (1/2;1/2)
V=3*1/2+8*1/2=5,5
Решим системы уравнений:
ОТВЕТ: оптимальная смешанная стратегия игрока
А – Sa=(0,375;0,625), игрока В – Sb=(0,5;0,5)
Слайд 23
Графический метод решения 2х2
Найдем оптимальную стратегию для первого
игрока (А):
а) построим систему координат:
б) по оси абсцисс откладывается
вероятность p1 ϵ [0,1], равная 1.в) по оси ординат – выигрыши игрока А при стратегии А2, а на прямой р = 1 – выигрыши при стратегии А1
г) находим точку пересечения прямых, которая и дает оптимальное решение матричной игры игрока А (ропт,v)
Слайд 24
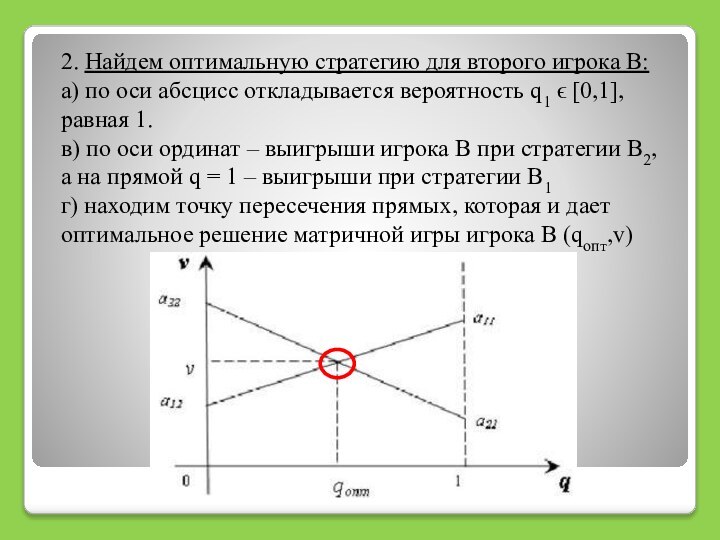
2. Найдем оптимальную стратегию для второго игрока В:
а)
по оси абсцисс откладывается вероятность q1 ϵ [0,1], равная
1.в) по оси ординат – выигрыши игрока В при стратегии В2, а на прямой q = 1 – выигрыши при стратегии В1
г) находим точку пересечения прямых, которая и дает оптимальное решение матричной игры игрока В (qопт,v)
Слайд 26
Решение:
Сначала необходимо определить, решается ли данная игра в
чистых стратегиях, то есть существует ли седловая точка или
нет.α = 4, β = 7,
при этом цена игры ⱱ ϵ [4,7]
α < β – игра не имеет седловой точки,
и поэтому имеет решение
в смешанных стратегиях.
Слайд 36
Используя алгебраический метод решения этой игры, получаем:
ОТВЕТ: оптимальные
смешанные стратегии игроков: Sa = (0,5; 0,5); Sb =
(0,17; 0,83)при цене игры v = 4,5





























