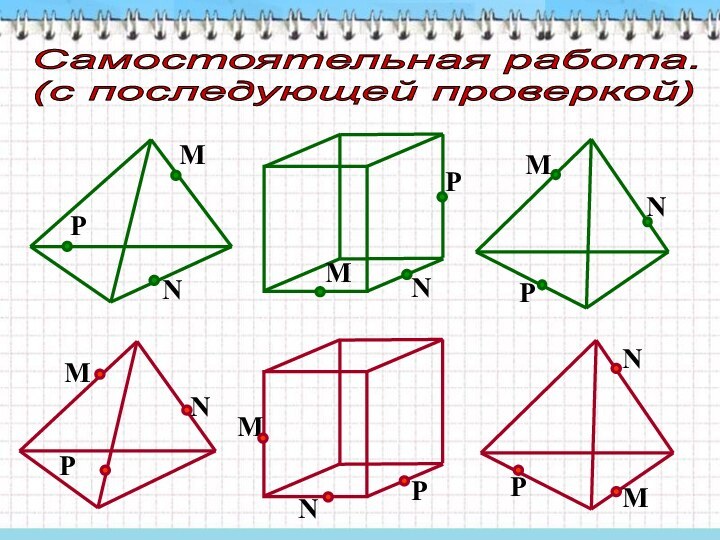
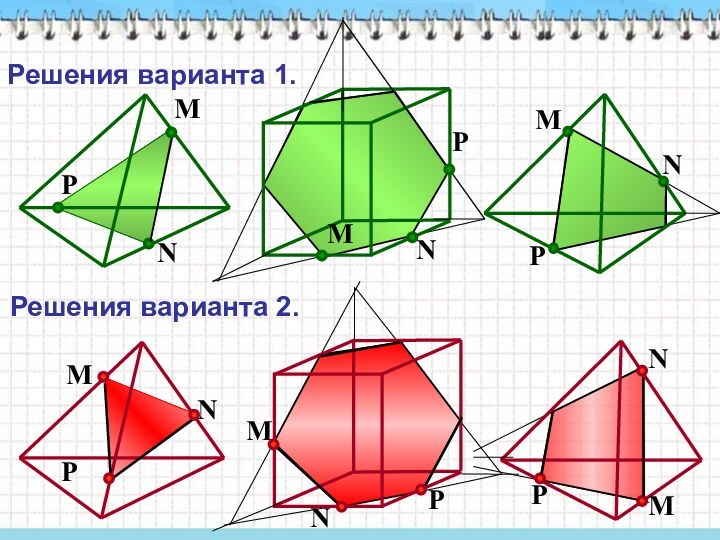
тел, формирует необходимые пространственные представления.
Стереометрия дает метод научного познания,
способствует развитию логического мышления.Стереометрия – сама по себе очень интересна. Она имеет яркую историю, связанную с именами знаменитых ученых