Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Правила сложения и умножения вероятностей и их следствия

Содержание

2. - надежность- система без резервирования- система с
3. Правило сложения для несовместных событий Вероятность суммы
4. По классическому определению :пусть в эксперименте с
5. Пример: в ящике 2 белых, 3 синих,
6. Важный частный случай – противоположные события Сумма
7. Часто на практике оценивается вероятность отказа объекта
8. ПримерЭксперимент: из коробки с 5 белыми и
9. Условная вероятность − P(A/B) или PB(A) есть
10. Правило умноженияВероятность произведения двух событий (т.е., их
11. Для независимых событий выполняется(по определению) условие независимости:
12. Правило умножения обобщается на любое число взаимонезависимых
13. Важные примерыРабота системы – произведение рабочих состояний
14. Если надежность элементов одинакова, т.е., pj =
15. Отказ системы независимых элементов, работающих параллельно –
16. В практических расчетах надежности и вероятности отказа
17. Пример:Вероятности отказа элементов системы q1 =
18. Вероятность наступления хотя бы одного из
19. Если событий лишь два, то вероятность «по
20. Скачать презентацию
21. Похожие презентации

- надежность- система без резервирования- система с резервированием- вероятность хотя бы одного из событий- правило сложения для совместных событий- неравенство вероятностей- формула Бернулли- формула гипотез ( полной вероятности)- формула Бейеса

Главная
Математика
Правила сложения и умножения вероятностей и их следствия

2. Правила сложения и умножения вероятностей и их

- надежность- система без резервирования- система с резервированием- вероятность хотя бы одного

Правило сложения для несовместных событий Вероятность суммы двух несовместных событий (т.е., одного

По классическому определению :пусть в эксперименте с равновозможными исходами mA элементарных событий

Пример: в ящике 2 белых, 3 синих, 4 красных шара и1 зеленый

Важный частный случай – противоположные события Сумма вероятностей противоположных событий равна единице

Часто на практике оценивается вероятность отказа объекта q, а затем определяется надежность

ПримерЭксперимент: из коробки с 5 белыми и 3 черными шарами извлекаются наугад

Условная вероятность − P(A/B) или PB(A) есть вероятность события А, вычисленная при

Правило умноженияВероятность произведения двух событий (т.е., их совместного наступления) равна вероятности одного

Для независимых событий выполняется(по определению) условие независимости: P(A/B) = P(А),

Правило умножения обобщается на любое число взаимонезависимых событий Вероятность совместного наступления независимых

Важные примерыРабота системы – произведение рабочих состояний всех k элементов (функционирует, только

Если надежность элементов одинакова, т.е., pj = p, j = 1…k →

Отказ системы независимых элементов, работающих параллельно – произведение отказов элементов. Откажет, только

В практических расчетах надежности и вероятности отказа наиболее удобно определить:1) для последовательной

Пример:Вероятности отказа элементов системы q1 = 0.1, q2 = 0.2 1)

Вероятность наступления хотя бы одного из нескольких независимых событий равна единице

Если событий лишь два, то вероятность «по крайней мере одного» можно определить

ПримерВероятности попасть в каждом из 2-х выстрелов 0.7 и 0.8.Вероятность хотя

Слайды презентации

Слайд 2 - надежность
- система без резервирования
- система с резервированием
-

- надежность- система без резервирования- система с резервированием- вероятность хотя бы

вероятность хотя бы одного из событий
- правило сложения для

совместных событий
- неравенство вероятностей
- формула Бернулли
- формула гипотез ( полной вероятности)
- формула Бейеса

Слайд 3 Правило сложения для несовместных событий
Вероятность суммы двух

Правило сложения для несовместных событий Вероятность суммы двух несовместных событий (т.е.,

несовместных событий (т.е., одного из них) равна сумме их

вероятностей:
P(A + B) = P(A) + P(B), если A ⋅ B = ∅

Из аксиоматического определения:

(только для него − «как получено»)

Эта сумма равна сумме двух первых

Слайд 4 По классическому определению :
пусть в эксперименте с равновозможными

По классическому определению :пусть в эксперименте с равновозможными исходами mA элементарных

исходами mA элементарных событий благоприятны событию А, mB –

событию B, (mA + mB) – событию (A + B).
Тогда:
P(A+B) = (mA + mB) / n = mA/n + mB/n = P(A) + P(B)

→ теорема доказана

Вероятность наступления одного из попарно несовместных событий
равна сумме
их вероятностей:

Обобщается на k несовместных событий (k > 2)

Слайд 5 Пример: в ящике 2 белых, 3 синих, 4

Пример: в ящике 2 белых, 3 синих, 4 красных шара и1

красных шара и
1 зеленый
Вероятность вынуть наугад шар цвета

российского флага: 0.2 + 0.3 + 0.4 = 0.9

+ 0.1 – вероятность вынуть зеленый шар = 1
– вероятность достоверного события ? –
«вынуть шар одного из возможных цветов»

Эта ситуация иллюстрирует следующее правило

Слайд 6 Важный частный случай –
противоположные события

Сумма вероятностей

Важный частный случай – противоположные события Сумма вероятностей противоположных событий равна

противоположных событий равна единице

P( A ) + P(A ) = 1

Слайд 7 Часто на практике оценивается вероятность отказа объекта q,

Часто на практике оценивается вероятность отказа объекта q, а затем определяется

а затем определяется надежность p
(вероятность безотказной работы)
p = 1

− q

Зависимые и независимые события. Условная и безусловная вероятность

Два события называют независимыми, если наступление одного из них не изменяет вероятности другого

Слайд 8 Пример
Эксперимент: из коробки с 5 белыми и 3

ПримерЭксперимент: из коробки с 5 белыми и 3 черными шарами извлекаются

черными шарами извлекаются наугад 2 шара.
События: В – 1-ый

шар черный, А – 2-ой шар белый.
2 разные схемы эксперимента:
а) «схема с возвращением»
(1-ый шар возвращается перед доставанием 2-го);
б) «схема без возвращения» (1-ый шар не возвращается)

Вероятности:
а) P(А) = 5 / 8 (не зависит от того, было ли В)
P(В) = 3 / 8 → А и В – независимые
б) P(А) = 4 / 7, если В не произошло, но
P(А) = 5 / 7, если В произошло
→ вероятность наступления А
зависит от наступления или не наступления В

Слайд 9 Условная вероятность − P(A/B) или PB(A)
есть вероятность

Условная вероятность − P(A/B) или PB(A) есть вероятность события А, вычисленная

события А, вычисленная при условии, что событие В имело

место.
Вероятность независимого события – безусловная
(абсолютная)

Как следует из определений вероятности,

условная вероятность равна вероятности совместного наступления двух событий, деленной на вероятность события, о котором предполагается, что оно имело место:
P(A/B) = P(A⋅B) / P(B)

Отсюда cледует
правило умножения вероятностей !

Слайд 10 Правило умножения
Вероятность произведения двух событий
(т.е., их совместного

Правило умноженияВероятность произведения двух событий (т.е., их совместного наступления) равна вероятности

наступления)
равна вероятности одного из них,
умноженной на условную вероятность

другого
при условии, что первое имело место:
P(A⋅B) = P(B) ⋅ P(A/B)
P(A⋅B) = P(А) ⋅ P(В/А)

Пример. В эксперименте с шарами по схеме (б), когда 1-ый шар не возвращается, P(A⋅B) = (3/8)⋅(5/7) = 15/56 − вероятность того, что 1-ый черный, а 2-ой белый

Слайд 11 Для независимых событий выполняется
(по определению) условие независимости:
P(A/B)

= P(А), P(В/А) = P(B)
В этом

случае правило умножения принимает следующую форму

P(A⋅B) = P(А) ⋅ P(В)
Вероятность произведения двух независимых событий равна произведению их вероятностей

Пример. В ситуации с возвращением шара (а)
P(A⋅B) = (5/8)⋅(3/8) = 15/64

Слайд 12 Правило умножения обобщается на любое число взаимонезависимых событий

Правило умножения обобщается на любое число взаимонезависимых событий Вероятность совместного наступления

Вероятность совместного наступления независимых событий равна
произведению их вероятностей:

P(А1A2… Аk) = P(А1) ⋅ P(А2) ⋅ … ⋅ P(Аk)

Все последующие формулы для расчета вероятностей событий можно рассматривать как следствия правил сложения и умножения

Слайд 13 Важные примеры
Работа системы – произведение
рабочих состояний всех

Важные примерыРабота системы – произведение рабочих состояний всех k элементов (функционирует,

k элементов
(функционирует, только если все действуют). Вероятность работы

системы в целом
определяется по правилу умножения.

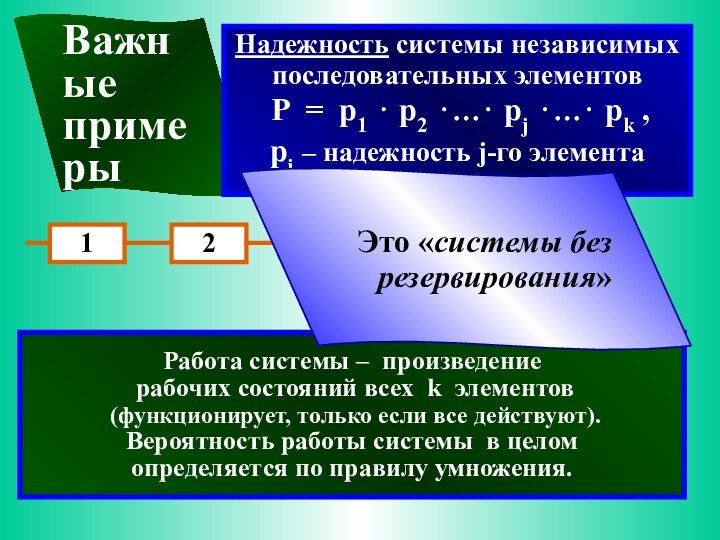
Надежность системы независимых последовательных элементов
P = p1 ⋅ p2 ⋅…⋅ pj ⋅…⋅ pk ,
pj – надежность j-го элемента

Это «системы без резервирования»

Слайд 14 Если надежность элементов одинакова, т.е.,
pj = p,

j = 1…k → P = pk
Надежность

системы без резервирования
падает с ростом количества элементов

Вероятность отказа такой системы:
Q = 1 – P = 1 – p1 p2…pj…pk

Слайд 15 Отказ системы независимых элементов, работающих параллельно – произведение

Отказ системы независимых элементов, работающих параллельно – произведение отказов элементов. Откажет,

отказов элементов.
Откажет, только когда откажут все элементы.
Это

« система с резервированием »

Вероятность отказа
Q = q1q2…qj…qk
Q = qk , если qj = q ( j = 1…k )
P = 1 – Q = 1 – q1 q2…qj…qk

Надежность системы с резервированием
растет с ростом количества элементов

Слайд 16 В практических расчетах надежности
и вероятности отказа
наиболее

В практических расчетах надежности и вероятности отказа наиболее удобно определить:1) для

удобно определить:

1) для последовательной системы – сначала P потом

Q

2) для параллельной системы –
сначала Q затем P

NB!

Слайд 17 Пример:
Вероятности отказа элементов системы q1 = 0.1,

q2 = 0.2
1) Если элементы последовательны,

то надежность P = p1⋅ p2 = (1 – q1)⋅(1 – q2)
= 0.9 ⋅ 0.8 = 0.72;
вероятность отказа Q = 1 – P = 0.28

2) Если элементы действуют параллельно,
то Q = q1 ⋅ q2 = 0.1⋅0.2 = 0.02;
надежность P = 1 – Q = 1 – 0.02 = 0.98

Q ← «откажет хотя бы 1»

P ← «работает хотя бы 1»

Слайд 18 Вероятность наступления хотя бы одного
из нескольких

Вероятность наступления хотя бы одного из нескольких независимых событий равна

независимых событий равна единице без произведения вероятностей противоположных событий:

P(A = A1 + A2 + … + Ak)
= 1– p(Ā1)⋅p(Ā2)⋅ … ⋅p(Āk)

Общее правило для расчета вероятности
«хотя бы одного из событий»
(как совместных, так и не совместных)

Слайд 19 Если событий лишь два, то вероятность
«по крайней

Если событий лишь два, то вероятность «по крайней мере одного» можно

мере одного» можно определить
по правилу сложения для совместных

событий
(при k > 2 существенно усложняется)

Вероятность наступления хотя бы одного
из двух совместных событий
равна сумме их вероятностей
без вероятности их совместного наступления:
P(A + B) = P(A) + P(B) – P(A⋅B)