Презентация на тему Правильные многогранники

по численности отряд сумел пробраться в самые глубины различных

наук.
Л. Кэрролл

тетраэдр

куб


октаэдр

додекаэдр


икосаэдр

указывается число граней:
«эдра» − грань;
«тетра» − 4;
«гекса»

− 6;
«окта» − 8;
«икоса» − 20;
«додека» − 12.

занимают видное место в философской картине мира, разработанной великим

мыслителем Древней Греции Платоном (ок. 428 – ок. 348 до н.э.).
Платон считал, что мир строится из четырёх «стихий» – огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников.

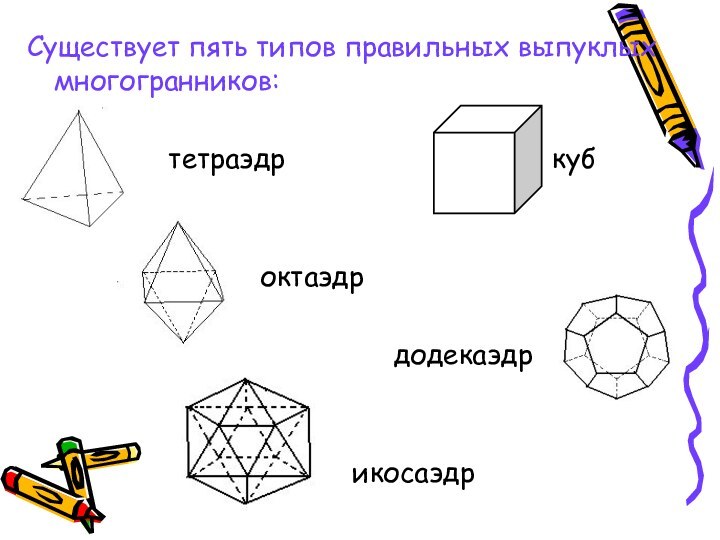
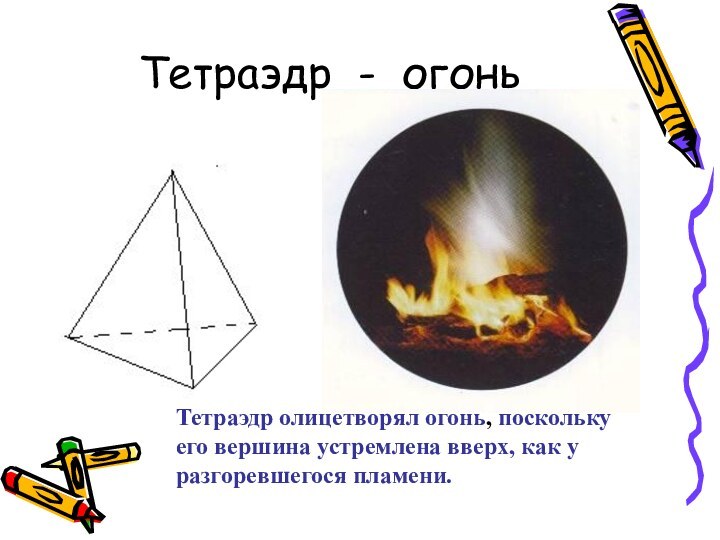
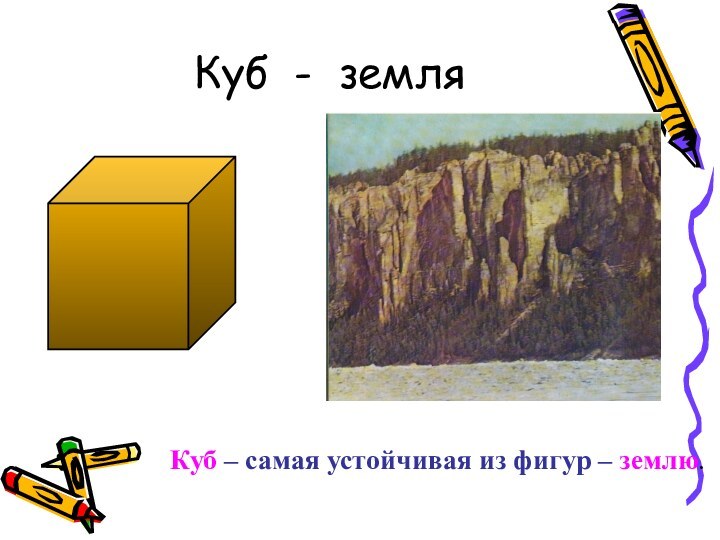
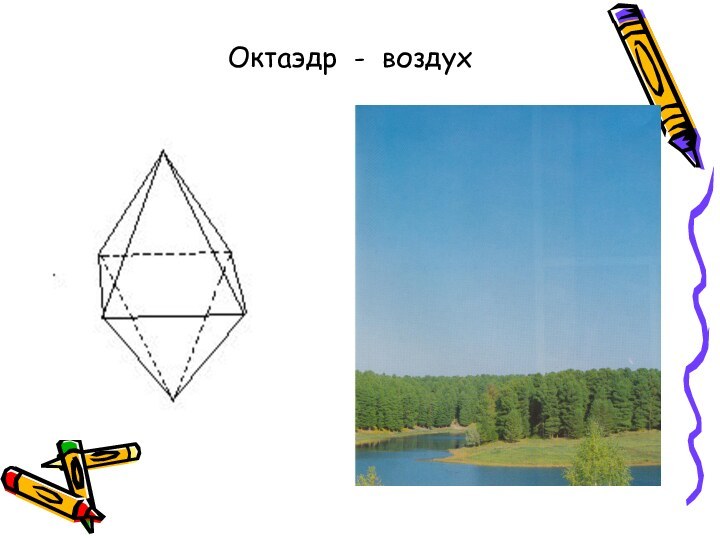
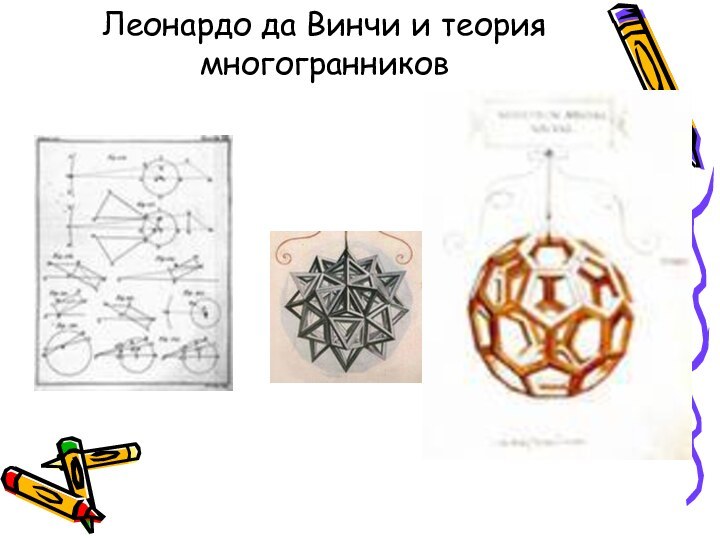
Правильные многогранники в философской картине мира Платона

устремлена вверх, как у разгоревшегося пламени.

– землю.

Октаэдр - воздух

воду

весь мир и почитался главнейшим.

Сам Евклид мог бы поучиться, познавая геометрию моих сот.»

(Из сказки «Тысяча и одна ночь»

скелет одноклеточного организма феодарии (Circjgjnia icosahtdra) по форме напоминает

икосаэдр.
Чем же вызвана такая природная геометризация феодарий? По-видимому, тем, что из всех многогранников с тем же числом граней именно икосаэдр имеет наибольший объём при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление водной толщи.
Правильные многогранники – самые «выгодные» фигуры. И природа этим широко пользуется. Подтверждением тому служит форма некоторых кристаллов.

и полуправильных многогранников. Куб передает форму кристаллов поваренной соли,

кристалл сернистого колчедана имеет форму додекаэдра, бор - икосаэдр

в десятки тысяч раз вирусы гриппа, полиомиелита, аденовирусы или

некоторые вирусы животных, то они кажутся мизерными сферами, или шариками. Отсюда их название — сферические или шаровидные. Но при внимательном, детальном изучении выясняется, что эти шарики состоят из отдельных частиц. Расположены частицы не как попало. Они образуют икосаэдр — правильный многогранник, поверхность которого образована двадцатью треугольными гранями.

именно икосаэдра? Оказывается, все дело в экономии. Допустим, вам

дали треугольные кирпичики и сказали, чтобы вы из них самым экономным способом сложили замкнутую оболочку. Строгие законы точной науки — математики подскажут вам, что в данном случае следует сложить икосаэдр. Природа, как самый гениальный математик, придала телу вирусов форму икосаэдра. По-видимому, дело здесь не только в экономии строительного материала.
Вирус в клетке должен совершить настоящий переворот, поработить ее и заставить работать на себя. Для этого он должен быть «умным». Он в миллионы раз меньше клетки. Весь план переворота нормальной жизни клетки должен быть тщательно записан, зашифрован в «мозгу» вируса — нуклеиновой кислоте. Поэтому «мозг» вируса должен быть как можно более объемистым, чтобы туда все уместилось. Но масса его ограничена. Для зашифровки тайны своей жизни в «мозгу» вируса оставлено совсем немного места. Таким способом достигается не только экономия строительного материала» но и -экономия генетической информации. Вирусы устроены не только просто, но и чрезвычайно целесообразно. Когда природа их лепила, она отбрасывала все ненужное, нерациональное.

Г и Р выполняется соотношение В + Г –

Р = 2