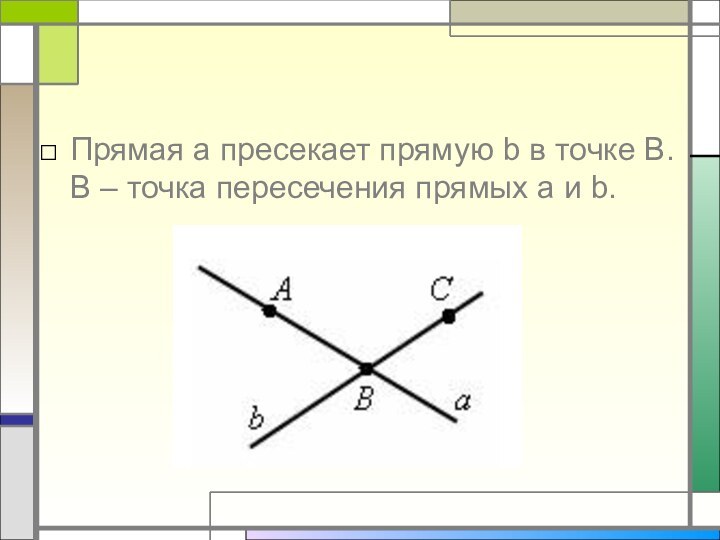
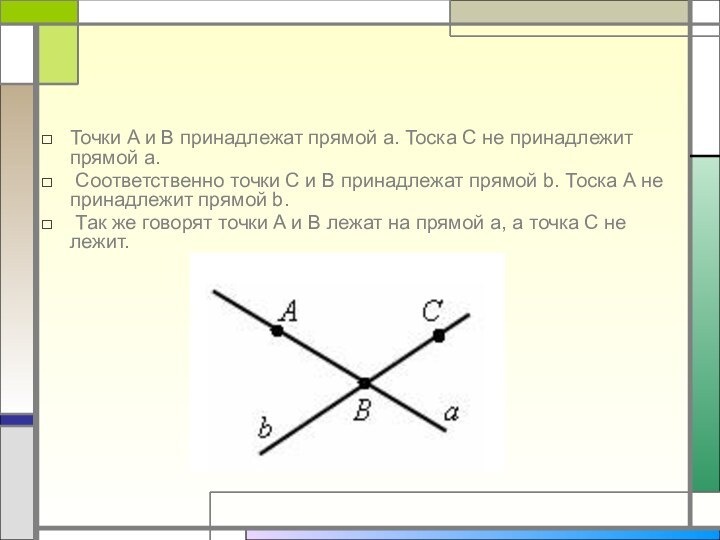
.
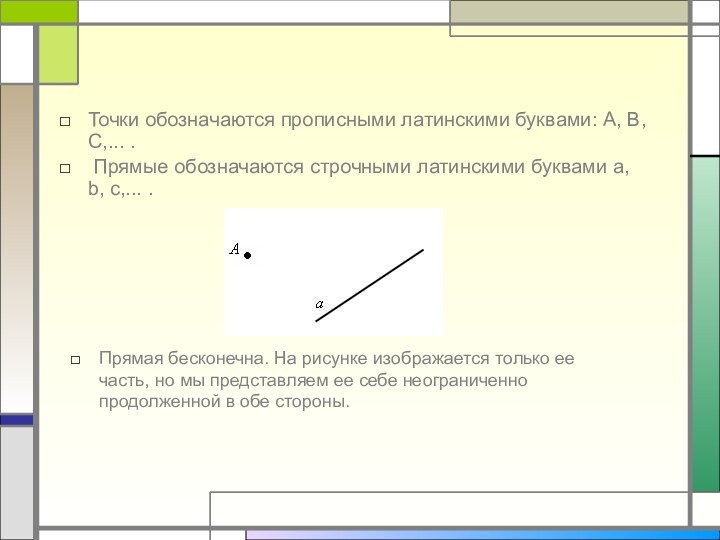
Прямые обозначаются строчными латинскими буквами a, b,
c,... .Прямая бесконечна. На рисунке изображается только ее часть, но мы представляем ее себе неограниченно продолженной в обе стороны.