- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ
Содержание
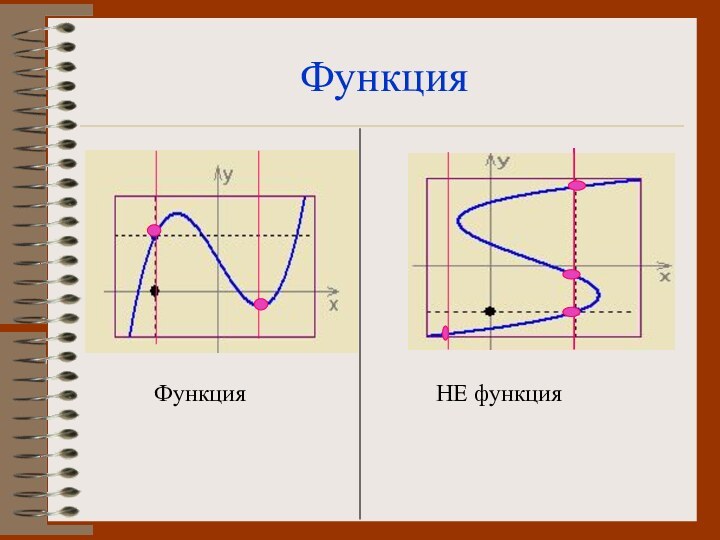
- 2. ФункцияФункция НЕ функция
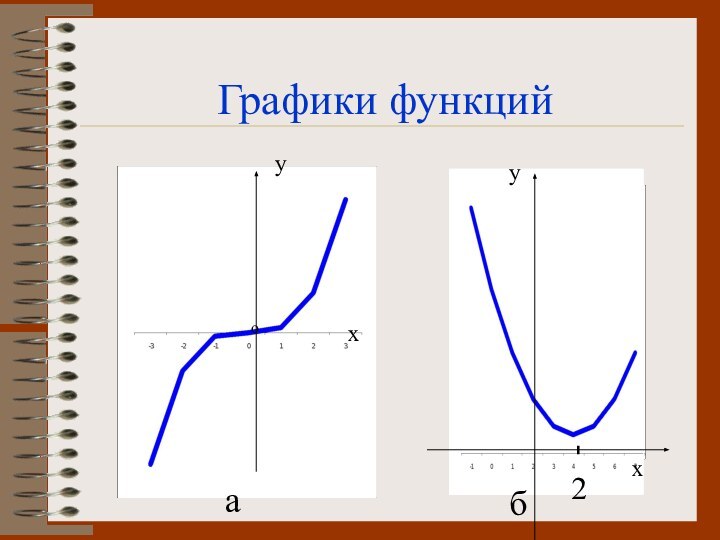
- 3. уаб2Графики функций
- 5. Возрастание и убывание функцииИду в гору. Функция возрастает на промежутке[b;a]Иду под гору. Функция убывает на промежутке[a;с]
- 6. Найдите производную функции:f(x)=3x³-2x²-3x+5f(x)=2x²+4x-4f(x)=sinxf(x)=sin2xf(x)=√xf(x)=2cosxf(x)=cosx+10
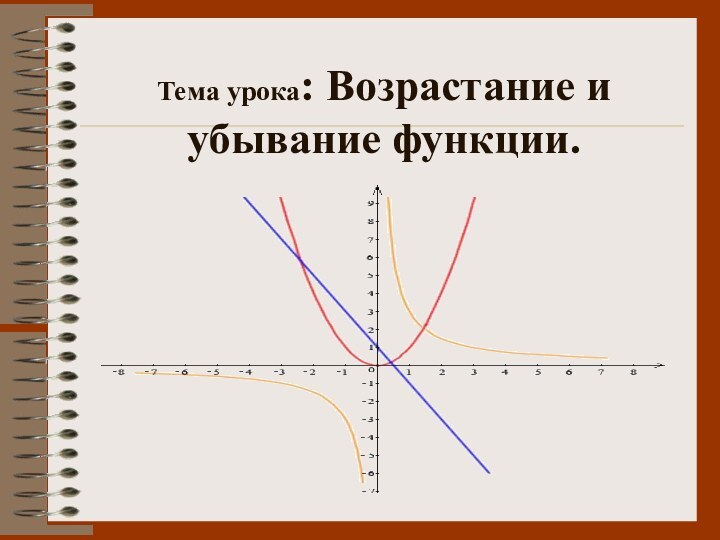
- 7. Тема урока: Возрастание и убывание функции.
- 8. Слушаю – забываю.Смотрю – запоминаю.Делаю – понимаю.Конфуций
- 9. f(x)=x³ - 6x² + 9x – 1f
- 10. Теорема: f(x) – непрерывна на I и
- 11. Доказательство:
- 12. f(x) = x³ - 6x² + 9x
- 13. f(x) = x³ - 6x² + 9x
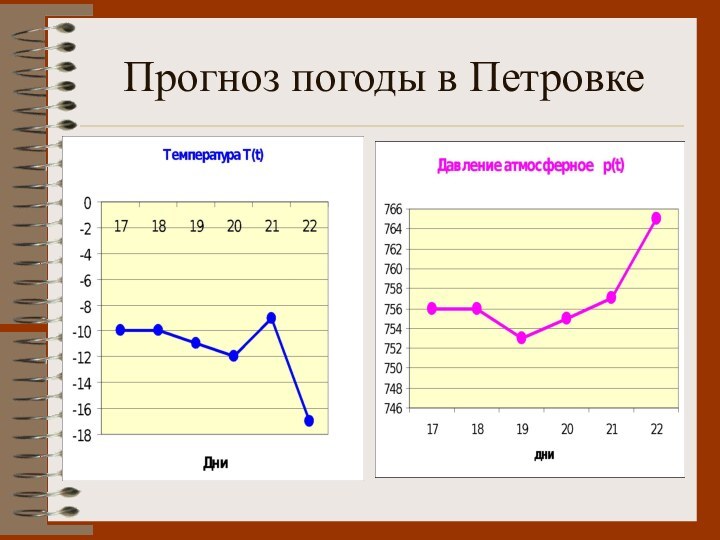
- 14. Прогноз погоды в Петровке
- 16. - обратиться к справочному материалу;- обратиться учебнику;-
- 17. Домашнее задание: п.5.5, № 5.52б, № 5.53б,№ 5.57б,№ 5.58б.
- 18. К высотам познанья! За кручей обрыв!Дороги орлам
- 19. Скачать презентацию
- 20. Похожие презентации
ФункцияФункция НЕ функция


![ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ Возрастание и убывание функцииИду в гору. Функция возрастает на промежутке[b;a]Иду под гору. Функция убывает на промежутке[a;с]](/img/tmb/12/1108325/24087a0fc7aa2a012d565d46dbebb5de-720x.jpg)











Слайд 6
Найдите производную функции:
f(x)=3x³-2x²-3x+5
f(x)=2x²+4x-4
f(x)=sinx
f(x)=sin2x
f(x)=√x
f(x)=2cosx
f(x)=cosx+10
Слайд 9
f(x)=x³ - 6x² + 9x – 1
f ´(x)
= 3x² - 12x + 9
Найдем критические точки:
f ´(x)
= 0, 3x² - 12x + 9 = 0x² - 4x + 3 = 0
x = 1 и х = 3
х
1
3
Слайд 10 Теорема: f(x) – непрерывна на I и имеет
f ´(x)
а) f ´(x) > 0, то f(x)
– возрастаетб) f ´(x) ˂ 0, то f(x) – убывает
в) f ´(x) = 0, то f(x) – постоянна(константа)
Слайд 12 f(x) = x³ - 6x² + 9x –
1
f ´(x) = 3x² - 12x + 9
Найдем критические
точки:f ´(x) = 0, 3x² - 12x + 9 = 0
x² - 4x + 3 = 0
x = 1 и х = 3
f ´(x) > 0, x ϵ (-∞; 1) и (3; + ∞)
f ´(x) ˂ 0, х ϵ (1; 3)
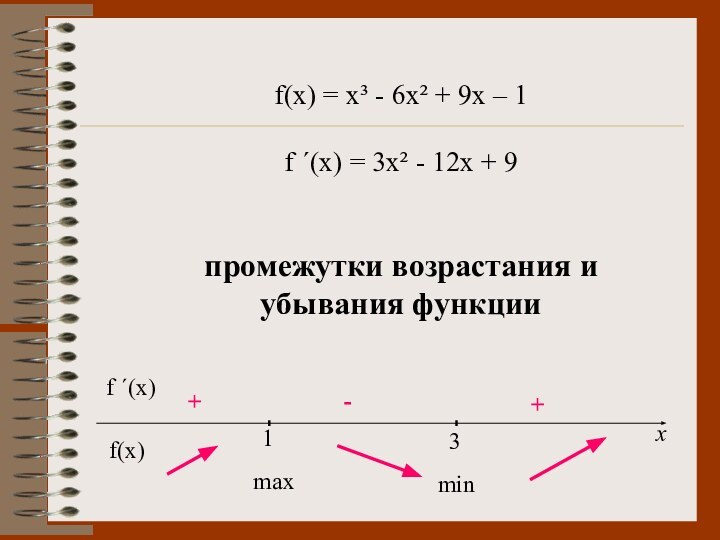
Слайд 13 f(x) = x³ - 6x² + 9x –
1
f ´(x) = 3x² - 12x + 9
промежутки возрастания
и убывания функциих
f ´(x)
f(x)
1
3
+
-
+
max
min
Слайд 16
- обратиться к справочному материалу;
- обратиться учебнику;
- проанализировать
выполнение аналогичных заданий;
- составить собственные примеры;
- обратиться за помощью
к учителю.План действий по локализации индивидуальных затруднений
Слайд 18
К высотам познанья!
За кручей обрыв!
Дороги орлам незнакомы.
Пройдет
человек лишь,
Но прежде открыв
Природы и чисел законы.
Искателей истин
судьба нелегка,Но тень их достанет в веках облака





























