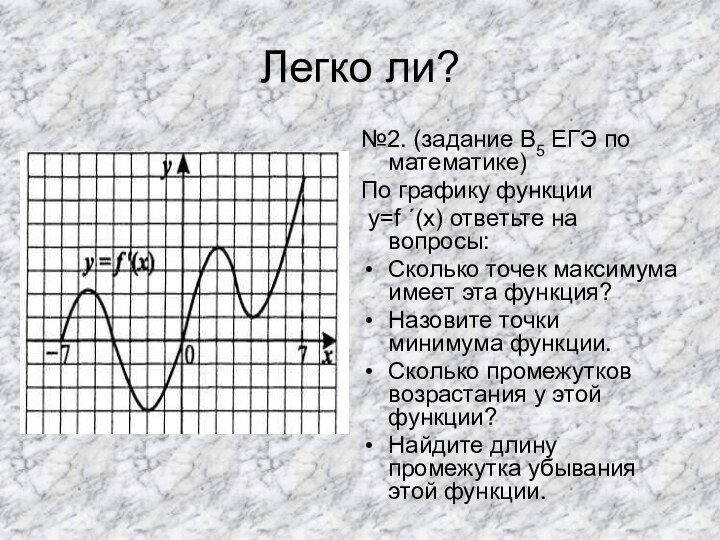
вопросы:
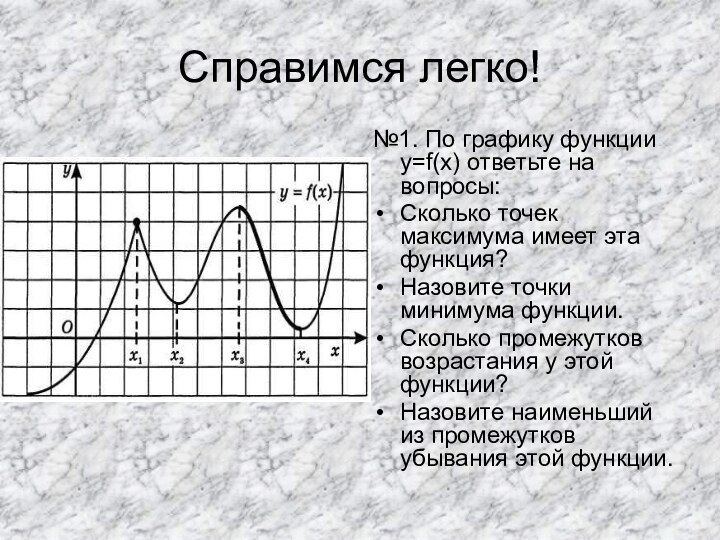
Сколько точек максимума имеет эта функция?
Назовите точки минимума функции.
Сколько
промежутков возрастания у этой функции?Назовите наименьший из промежутков убывания этой функции.






![Применение производной для исследования функции №1. Непрерывная функция y=f(x) задана на [-10;11]. На рисунке изображён](/img/tmb/13/1268556/090086e30be1bf52b064c092c1e6c517-720x.jpg)