Слайд 2
Мета:
ПРАКТИЧНА:
Формувати вміння аналізувати інформацію, аналізувати особисті пізнавальні та
практичні дії;
Розвивати навички групової роботи;
Підвищувати рівень активності і самостійності;
Формувати
вміння і навики роботи з Інтернет – ресурсами, розвивати спеціальні дослідницькі вміння і навики.
ОСВІТНЯ:
Познайомити учнів з пірамідою як з геометричним тілом;
Значення піраміди з історичної і математичної точки зору;
Показати взаємозв’язок вивчаємих на уроці тем з навколишнім світом і оточуючим нас побутом.
РОЗВИВАЮЧА:
Розвивати пізнавальний інтерес до математики, вміння висловлювати свою думку, художнє бачення, навички режисури.
ВИХОВНА:
Сприяти вихованню активного мислення, комунікативних якостей учнів;
Виховувати творче мислення, всебічно розвинуту особистість;
Слайд 3
Актуальність проблеми:
Комп’ютерні технології інтенсивно запроваджуються як традиційних галузях
виробництва, так і в нових, виникнення яких неможливо уявити
без застосування комп’ютерної техніки.
Розробка проекту з об’єднанням істрорії, геометрії і інформатики, дозволила раціонально об’єднати теоретичні знання учнів з їх творчими можливостями та розкриттям багатьох талантів при створенні відеофільму. Цей проект допоміг розкрити у учнів багатий творчий та духовний потенціал, показати, що спостерігати самим, дослідувати та пізнавати предмети самостійно, сприяє становленню цікавої, всебічно розвинутої особистості, а також, що математика не суха наука,а дуже глибока і цікава.
Слайд 4
ЕТАПИ ПРОЕКТУ:
І. Підготовчий етап: визначення проблеми, мети й
завдань
ІІ. Відбір матеріалу: зібрати інформацію про історію пірамід, піраміду
– геометричне тіло, піраміда в сучасному житті.
ІІІ. Презентація: результати пошуку інформації – слайди.
Продукт: презентація, електронна фотогалерея.
Термін реалізації: 2 тижні
Слайд 5
Джерела інформації:
підручники, енциклопедії, сучасна література,
інтернет-ресурси, моделі
пірамід, фотоапарат; комп’ютер зі
спеціальним програмним забезпеченням.
Очікувані результати:
Учні навчаться
збирати та аналізувати цікавий та необхідний
матеріал з заданої теми, ставити мету та раціонально добиватися її, навчаться планувати зміст діяльності, оцінювати свої можливості і зусилля, висловлювати свою думку, робити висновки. Навчаться справедливо оцінювати свою роботу і роботу всієї групи, навчаться публічно виступати при захисті проекту, а також розширять свій кругозір, поглиблять знання з математики при роботі з додатковою літературою, та за допомогою комп’ютерних технологій поглиблять навички при роботі на уроках інформаційних технологій.
Слайд 6
Критерії успіху:
Проект буде вважатися успішним, якщо його результати
зацікавлять учнів і інших вчителів, а головне, якщо його
будуть використовувати в роботі учителі та учні для поглиблення своїх знань.
Кількість учасників проекту: 5 учнів.
Роль викладача: корегувач дій, консультант.
Роль учнів: 2 - історики, 5 - математиків, 3 - дослідники.
Слайд 7
Проект з математики
“Піраміди”
Слайд 8
Піраміда в історії
Усе на світі боїться часу, а
час боїться пірамід.
Слайд 9
Египетські піраміди – одне із семи чудес світу
найбільший архітектурний пам'ятник Стародавнього Єгипту
Слайд 11
Висота: 147м
Основа: 234х234м
Площа основи: 5,4 га
Висота: 137м
Основа: 234х234м
Площа
основи: 5,4 га
Велика піраміда Хеопса (Хуфу)
Старовинна назва:
Горизонт Хуфу
Слайд 12
У піраміді Хеопса має місце теорема Піфагора, золота
пропорція. На світанку вона має колір рожевого персика, а
в холодному світлі місяця нагадує вкриту снігом гірську вершину.
Слайд 13
Грані пірамід дуже точно орієнтовані по сторонах світу.
Висота піраміди Хеопса, яку будували 30 років становить 1/1000000000
частину відстані від Землі до Сонця. Якщо довжину обводу основи піраміди Хеопса поділити на її подвоєну висоту, то вийде 3,14159 – число π з великою точністю.
Слайд 14
Площа кожної з граней піраміди дорівнює квадрату її
висоти.
Слайд 15
Порівняння величі споруд
Собор святого
Петра в Римі
Піраміда
Джосера
Піраміда Хеопса
Слайд 16
Сяюча піраміда Снофру
2612—2589 рр. до н. е.
Слайд 17
Піраміда Сонця Теотіукан (Південна Америка)
Слайд 19
Загублені піраміди Китаю. Велика мармурова піраміда.
Слайд 21
З пірамідами пов'язано дуже багато легенд, таємниць, які
ще потрібно розгадати людству.
Єгиптологи висунули ще одну гіпотезу: піраміди
є своєрідними посиланнями, які повинні через тисячоліття донести якусь інформацію нащадкам.
Слайд 23
ОЗНАЧЕННЯ. ПІРАМІДОЮ НАЗИВАЄТЬСЯ МНОГОГРАННИК, ЩО СКЛАДАЄТЬСЯ З ПЛОСКОГО
МНОГОКУТНИКА – ОСНОВИ ПІРАМІДИ, ТОЧКИ, ЯКА НЕ НАЛЕЖИТЬ ПЛОЩИНІ
ОСНОВИ – ВЕРШИНИ ПІРАМІДИ, ТА ВСІХ ВІДРІЗКІВ, ЩО СПОЛУЧАЮТЬ ВЕРШИНУ ПІРАМІДИ З ТОЧКАМИ ОСНОВИ.
Слайд 24
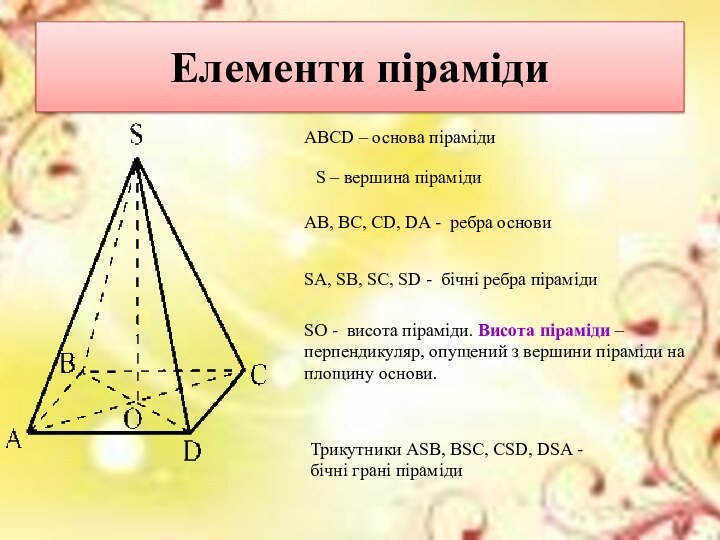
Елементи піраміди
ABCD – основа піраміди
S – вершина піраміди
AB,
BC, CD, DA - ребра основи
SA, SB, SC, SD
- бічні ребра піраміди
SO - висота піраміди. Висота піраміди –перпендикуляр, опущений з вершини піраміди на площину основи.
Трикутники ASB, BSC, CSD, DSA - бічні грані піраміди
Слайд 26
Кути у піраміді
M
плоский кут при вершині ∠ASE;
кут
нахилу бічного ребра до площини основи ∠ SAO; двогранний
кут при бічному ребрі ∠DFA;
кут нахилу бічної грані до площини основи ∠SKO.
OF - відстань від основи висоти до бічного ребра.
OM - відстань від основи висоти до бічної грані.
Слайд 27
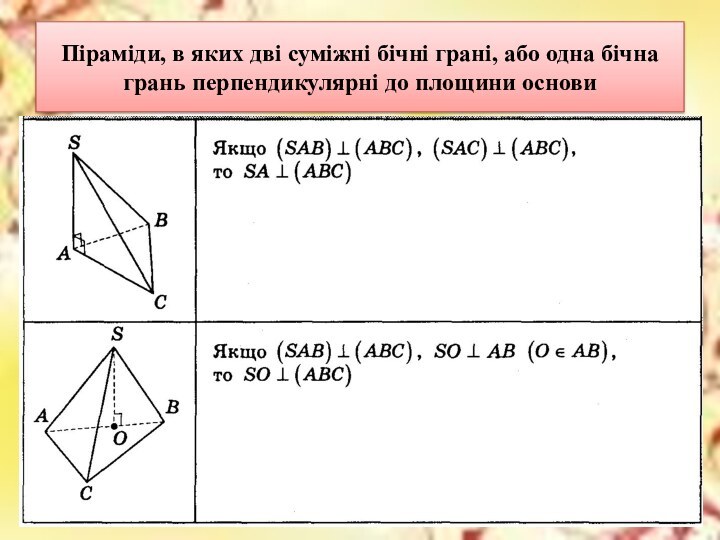
Піраміди, в яких дві суміжні бічні грані, або
одна бічна грань перпендикулярні до площини основи
Слайд 28
Правильна піраміда
Піраміда називається правильною,
якщо її основою є правильний
многокутник,
а основа висоти
збігається з центром цього многокутника
Віссю правильної піраміди
називається пряма, яка містить її висоту
У правильній піраміді всі бічні ребра рівні, бічні грані – рівнобедрені трикутники.
Висота бічної грані правильної піраміди, проведена з її вершини, називається апофемою.
Бічна поверхня правильної піраміди дорівнює добутку півпериметра основи на апофему.
Бічною поверхнею піраміди називається сума площ її бічних граней.
Слайд 29
• всі бічні грані нахилені до площини основи
під одним і тим самим кутом;
• усі бічні грані
мають однакові висоти;
• висоти бічних граней утворюють однакові кути з висотою піраміди;
• бічні грані рівновіддалені від основи висоти, — то
основа висоти лежить у центрі кола, вписаного в основу піраміди.
Якщо виконується хоча б одна з таких умов:
Слайд 30
Якщо виконується хоча б одна з таких умов:
• усі бічні ребра піраміди рівні;
• усі
бічні ребра нахилені до площини основи під одним і тим самим кутом;
• усі бічні ребра утворюють однакові кути з висотою піраміди;
• усі бічні ребра рівновіддалені від основи висоти, — то
основою висоти піраміди є центр кола, описаного навколо основи піраміди
Слайд 31
Ну що там храм прадавній Артеміди,
Колос Родоський, це
якісь дива!
Дивіться: це фігура – піраміда,
Краса її завжди жива.
Нахилені
до купи грані
Вершину творять горду і стрімку.
Усе довершене у ній, прегарній,
Хіба забути нам таку?
Піраміди в сучасному житті
Слайд 34
Дизайнери-архітектори використовують пірамідальні форми при побудові будинків, ліхтарів
на вулиці, дахів на каплицях, церков.
Слайд 38
Використання пірамід з метою оздоровлення
Слайд 39
Вінницька чудесна гранітна піраміда вже відома на весь
світ
Слайд 40
В Європі зараз є спеціальні овочесховища, зроблені у
вигляді пірамід. Вважається, що смакові якості продуктів, які зберігаються
на таких базах, підвищується, а врати зменшуються на 4-10%.
Слайд 42
Пірамідальні форми також використовують при виготовленні упаковки для
продуктів в харчовій промисловості
Слайд 43
Предмети побуту пірамідальної форми