3. Пример 3. Пример 3. Пример
№14. Пример №2
5. Выполнить построение
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Произведение функций
Содержание
- 2. Содержание 1. Определение 2. Алгоритм
- 3. Определение Произведением двух функций f(x) и
- 4. Алгоритм построения1) Построить график функций y=f(x)2) Построить
- 5. Пример №1Построить функцию y=x.x2
- 6. 1) Строим график функции y=x
- 7. x Y 1 2 -1 -1 1
- 8. 2) Строим график функции y=x2 в той
- 9. x Y 1 2 -1 -1 1
- 10. 3) В каждой точке перемножить
- 11. x Y 1 2 -1 -1 1
- 12. Пример №2Построить функцию y=x . cosx
- 13. Функция y=x .cosx является нечетной
- 14. 1)Строим график функции y=x. Графиком
- 15. x Y 1 2 -1 -1 1
- 16. 2)Построим график функции y=cosx.
- 17. x Y 1 2 -1 -1 1
- 18. 3) В каждой точке перемножить длины отрезков,
- 19. x Y 1 2 -1 -1 1
- 20. Скачать презентацию
- 21. Похожие презентации
Содержание 1. Определение 2. Алгоритм построения 3. Пример 3. Пример 3. Пример №1 4. Пример №2 5. Выполнить построение
Слайд 3
Определение
Произведением двух функций f(x) и g(x)
называется функция h(x) с областью определения, являющейся общей частью
областей определения f(x) и g(x), при этом значения функции h(x) = f(x) . g(x).
Слайд 4
Алгоритм построения
1) Построить график функций y=f(x)
2) Построить график
функции y=g(x) в той же системе координат.
3) В
каждой точке перемножить длины отрезков, изображающие ординаты графиков, и построить отрезок полученной длины с учетом знака произведения. Множество точек с полученными ординатами представляют график функции h(x)=f(x) . g(x)
Слайд 6
1) Строим график функции y=x
Графиком
этой функции является прямая.
Биссектриса I и
III координатных углов.
Слайд 8
2) Строим график функции y=x2 в той же
системе координат.
Графиком этой функции является парабола
Ветви направлены вверх (т.к. a=1>0)
Вершина находится в точке O(0;0).
Слайд 10
3) В каждой точке перемножить длины
отрезков, изображающие ординаты графиков, и построить отрезок полученной длины
с учетом знака произведения.
Слайд 11
x
Y
1
2
-1
-1
1
2
-2
-2
x=1 y=1*1=1
x=-1 y=1*(-1)=-1
x=0 y=0*0=0
x=-1,5
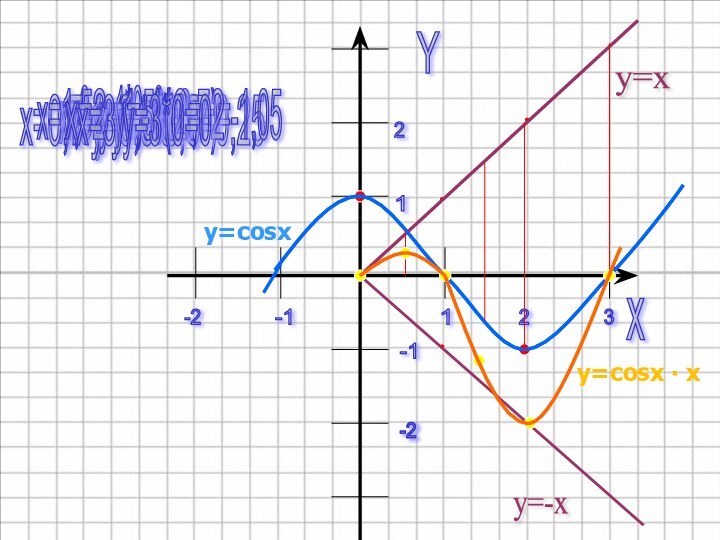
y=-1,5*2,25=-3,375 x=1,5 y=2*1,5=3
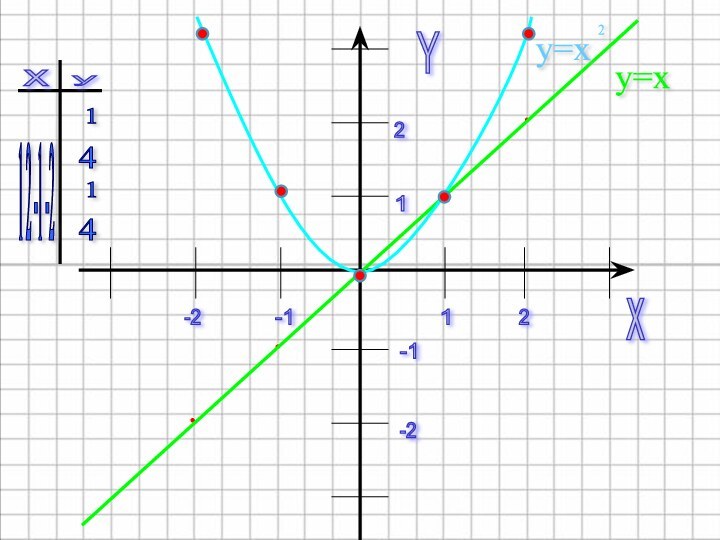
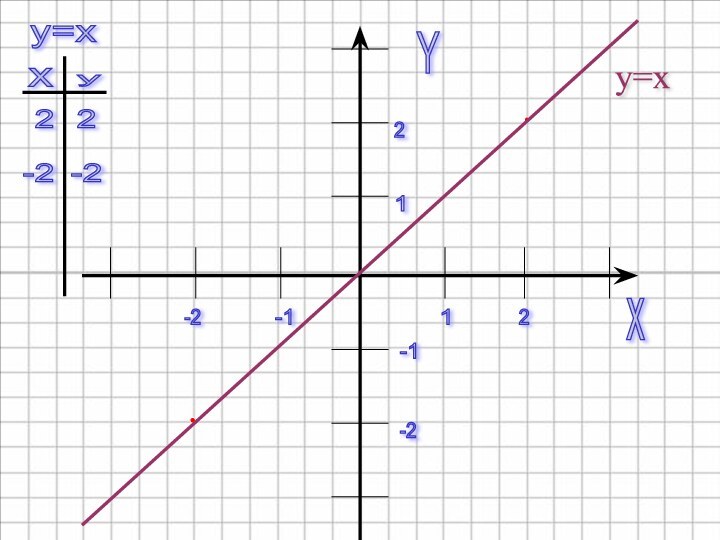
y=x
y=x
2
y=x ∙ x
2
Слайд 13 Функция y=x .cosx является нечетной (она
представляет собой произведение четной и нечетной функций), поэтому ее
график будет симметричным относительно начала координат и его достаточно построить лишь для х>0.
Слайд 14
1)Строим график функции y=x.
Графиком этой
функции является прямая.
Биссектриса I и III координатных углов.
Слайд 16
2)Построим график функции y=cosx.
Заметим, что в точках x=П/2+Пk, в которых cosx=0, функция
равна нулю. В точках x=2Пk, где cosx=1, произведение равно 2Пk, т.е. эти точки лежат на прямой y=x, а в точках x=П+Пk, где cosx=-1, произведение равно –(П+2Пk), т.е. эти точки лежат на прямой y=-x.
Слайд 18
3) В каждой точке перемножить длины отрезков, изображающие
ординаты графиков, и построить отрезок полученной длины с учетом
знака произведения.
Слайд 19
x
Y
1
2
-1
-1
1
2
-2
-2
y=x
y=-x
x=0 y=1*0=0
x=1 y=1*0=0
x=0,7
y=0,5*0,5=0,25 x=1,5 y=1,5*(-0,7)=-1,05
x=2 y=-1*2=-2
-2
3
x=3 y=3*0=0
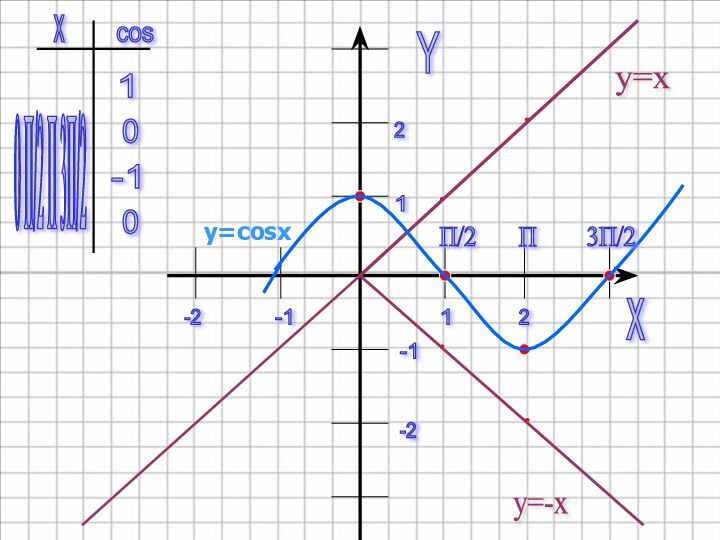
y=cosx
y=cosx ∙ x
