Слайд 2
«Правильных многогранников вызывающе мало,
но этот весьма скромный по численности отряд сумел пробраться
в самые глубины различных наук».
Льюис Кэрролл
Слайд 3
На уроках математики вы уже встречались с
многогранниками. Сегодня я хочу пригласить вас в увлекательный раздел
геометрии – теорию правильных многогранников. Вам предстоит ответить на многие вопросы: Какие многогранники называются правильными? Сколько их существует? Что такое характеристика Эйлера? И многое, многое другое. Данный материал пригодится вам при изучении геометрии в 10-11 классах
Слайд 4
Многогранники
Многогранники представляют собой простейшие тела в пространстве, подобно
тому как многоугольники – простейшие фигуры на плоскости. Детские
кубики, архитектурные сооружения, ювелирные украшения – оглянитесь вокруг, и вы найдете многогранники повсюду.
Слайд 5
Многогранники
Многогранник - это часть пространства, ограниченная плоскими многоугольниками
–гранями. Стороны и вершины граней называют ребрами и вершинами
многогранника.
Слайд 6
Правильные многогранники
Правильный многогранник - выпуклый многогранник грани которого
являются правильными многоугольниками с одним и тем же числом
сторон и в каждой вершине которого сходится одно и тоже число рёбер.
Существует всего пять правильных многогранников
Слайд 7
Правильные многогранники
Правильный тетраэдр (четырехгранник) — многогранник, составленный из четырех
правильных треугольников, в каждой его вершине сходятся 3 ребра
Слайд 8
Правильные многогранники
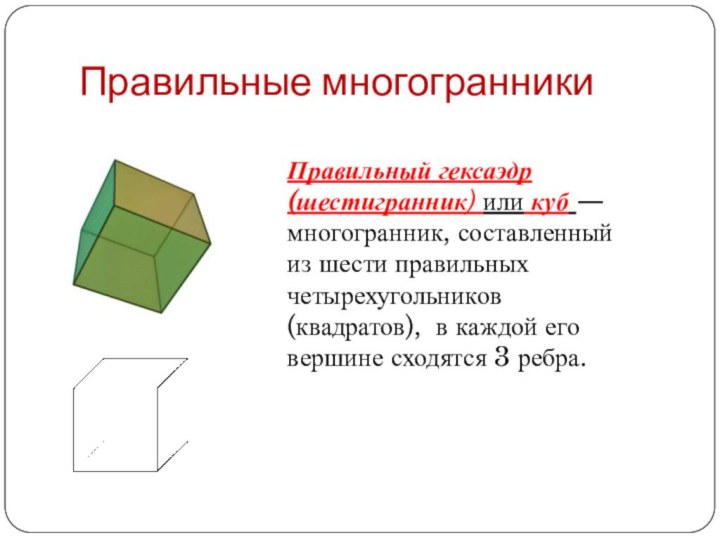
Правильный гексаэдр (шестигранник) или куб — многогранник, составленный из шести
правильных четырехугольников (квадратов), в каждой его вершине сходятся 3
ребра.
Слайд 9
Правильные многогранники
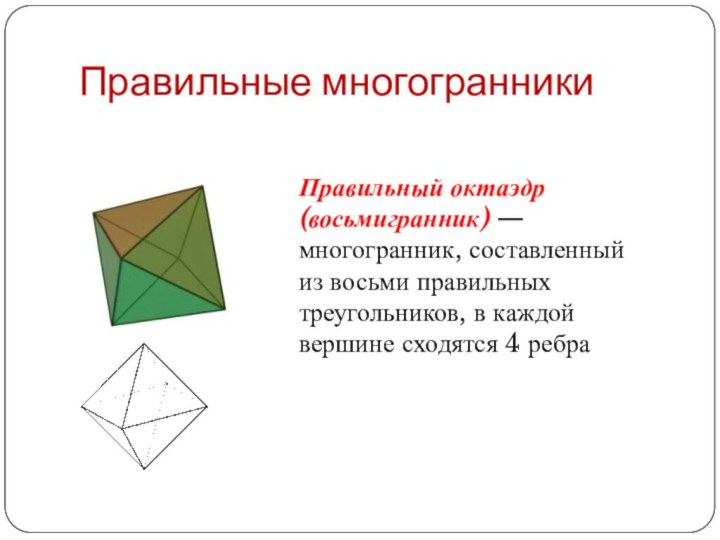
Правильный октаэдр (восьмигранник) — многогранник, составленный из восьми
правильных треугольников, в каждой вершине сходятся 4 ребра
Слайд 10
Правильные многогранники
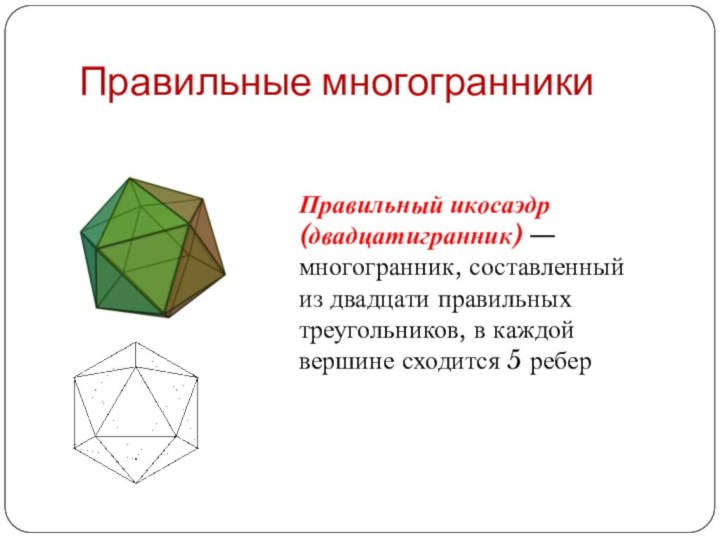
Правильный икосаэдр (двадцатигранник) — многогранник, составленный из двадцати
правильных треугольников, в каждой вершине сходится 5 ребер
Слайд 11
Правильные многогранники
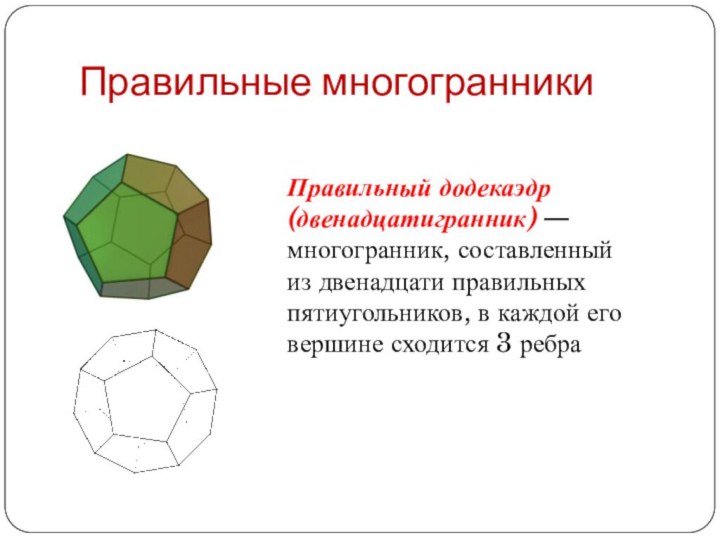
Правильный додекаэдр (двенадцатигранник) — многогранник, составленный из двенадцати
правильных пятиугольников, в каждой его вершине сходится 3 ребра
Слайд 12
Леонард Эйлер
(1707 – 1783 гг.)
немецкий математик и физик
Теорема
Эйлера
Для любого выпуклого многогранника справедливо соотношение: Г+В-Р=2.
Г-число
граней, В-число вершин, Р-число рёбер.
Теорема Эйлера
Для любых выпуклых многогранников существует некоторое постоянное соотношение между числом вершин, граней и ребер, которое было установлено Леонардом Эйлером (1707-1783).
Слайд 13
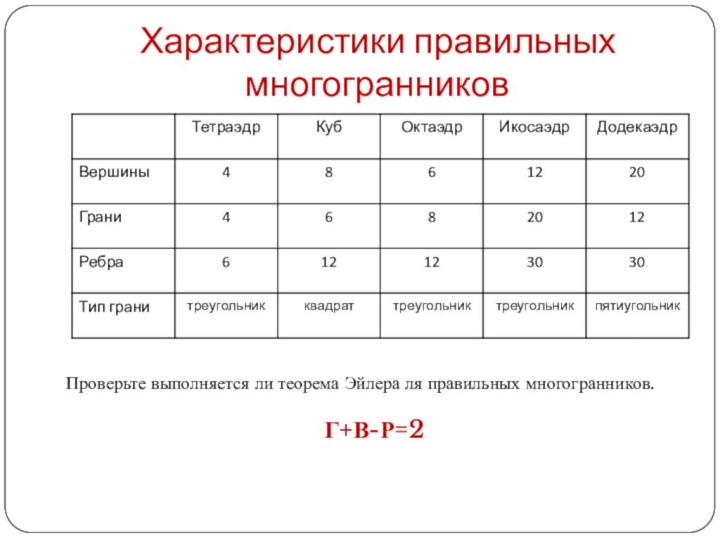
Характеристики правильных многогранников
Проверьте выполняется ли теорема Эйлера ля
правильных многогранников.
Г+В-Р=2
Слайд 14
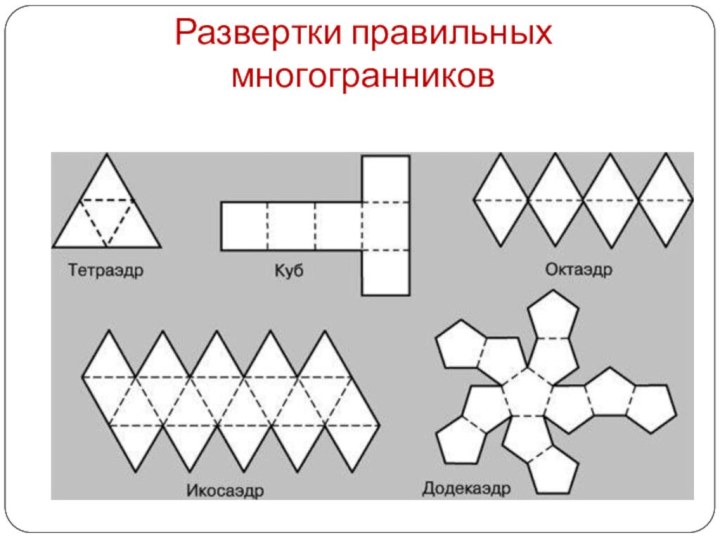
Развертки правильных многогранников
Слайд 15
Из истории правильных многогранников
Правильные многогранники с древних времен
привлекали к себе внимание ученых, строителей, архитекторов и многих
других. Их поражала красота, совершенство, гармония этих многогранников. Пифагорейцы считали эти многогранники божественными и использовали их в своих философских сочинениях о существе мира. Они считали, что элементы первооснов бытия имеют форму правильных многогранников, а именно:
Евклид
3 век до н.э
Слайд 16
Тетраэдр - Огонь
Гексаэдр - Земля
Октаэдр - Воздух
Икосаэдр
- Вода
Додекаэдр - Вселенная
Слайд 17
Платоновы тела
Платон
428-348 гг. до н.э.
Греческая математика, в которой
впервые появилась теория многогранников, развивалась под большим влиянием знаменитого
мыслителя Платона. Философ - идеалист Платон изложил в своих трудах учение о правильных многогранниках .
С тех пор правильные многогранники стали называться
Платоновыми телами
Слайд 18
Евклид
3 век до н.э.
Правильным многогранникам посвящена последняя, XIII
книга знаменитого труда Евклида. XIII книгу Евклида историки математики
называют «венцом «Начал». Здесь установлено существование всех пяти типов правильных многогранников, путей их построения и доказано, что других правильных многогранников не существует.
Слайд 19
Двойственность правильных многогранников
Возьмем любой куб и рассмотрим многогранник
с вершинами в центрах его граней. Как нетрудно убедиться,
получим октаэдр
Центры граней октаэдра служат вершинами куба
Существуют две пары правильных многогранников, для которых число вершин одного равно числу граней другого – октаэдр и куб, икосаэдр и додекаэдр. Такие многогранники называются двойственными. Тетраэдр двойствен самому себе.
Слайд 20
Двойственность правильных многогранников
Икосаэдр и додекаэдр также являются двойственными
многогранниками
Двойственным многогранником к тетраэдру является сам тетраэдр
Слайд 21
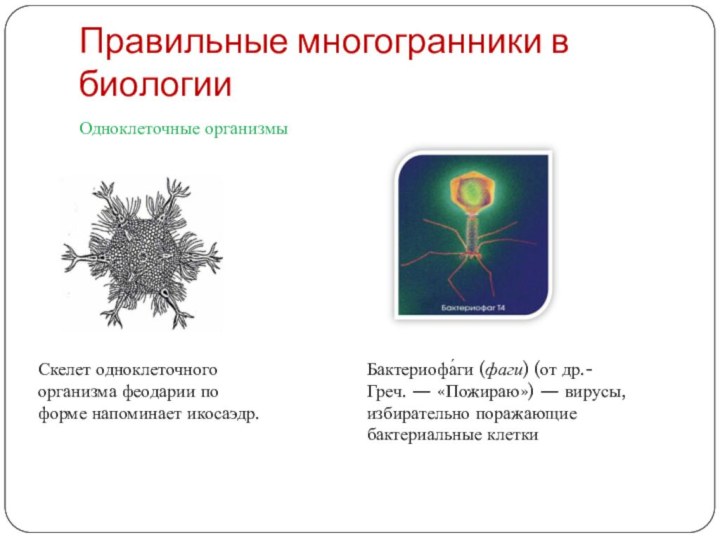
Правильные многогранники в биологии
Одноклеточные организмы
Скелет одноклеточного
организма феодарии по форме напоминает икосаэдр.
Бактериофа́ги (фаги) (от
др.- Греч. — «Пожираю») — вирусы, избирательно поражающие бактериальные клетки
Слайд 22
Правильные многогранники в биологии
Вирусы
Именно икосаэдр оказался в центре
внимания биологов в их спорах относительно формы вирусов. Вирус
не может быть совершенно круглым, как считалось ранее.
На картинке изображен вирус поражающий ценные растения
Вирусы, построенные только из нуклеиновой кислоты и белка, могут походить на жесткую палочкообразную или гибкую нитевидную спираль, точнее на правильный двадцатигранник, или икосаэдр.
Слайд 23
Правильные многогранники в биологии
ДНК
ДНК генетического кода жизни –
представляет собой четырехмерную развертку (по оси времени) вращающегося додекаэдра!
В процессе деления яйцеклетки сначала образуется тетраэдр из четырех клеток, затем октаэдр, куб и, наконец, додекаэдроикосаэдрическая структура гаструлы.
Слайд 24
Кристаллы
эти твёрдые тела имеют естественную форму правильных
многогранников
Квасцы
Алмаз
Поваренная соль
Пирит
Слайд 25
Правильные многогранники в искусстве
На картине художника Сальвадора Дали
«Тайная Вечеря» Христос со своими учениками изображён на фоне
огромного прозрачного додекаэдра.
Форму додекаэдра, по мнению древних, имела ВСЕЛЕННАЯ , т.е. они считали, что мы живём внутри свода, имеющего форму поверхности правильного додекаэдра.
Слайд 26
Правильные многогранники в искусстве
Знаменитый художник, увлекавшийся геометрией,
Альбрехт
Дюрер
(1471- 1528),
в известной гравюре
«Меланхолия»
на переднем плане
изобразил додекаэдр
Слайд 27
Правильные многогранники в искусстве
Рисунки тел Платона, выполненные Леонардо
да Винчи к книге Луки Пачоли
«О божественной пропорции».
Венеция. 1509 г.
Слайд 28
Ма́уриц Корне́лис Э́шер
(17 июня 1898 — 27 марта
1972) — нидерландский художник-график.
Правильные геометрические тела - многогранники -
имели особое очарование для Эшера. В его многих работах многогранники являются главной фигурой и в еще большем количестве работ они встречаются в качестве вспомогательных элементов.
Правильные многогранники в искусстве
Куб с волшебными лентами
Слайд 29
Правильные многогранники в искусстве
На гравюре "Четыре тела"
Эшер изобразил пересечение основных правильных многогранников, расположенных на одной
оси симметрии, кроме этого многогранники выглядят полупрозрачными, и сквозь любой из них можно увидеть остальные
Фигуры, полученные объединением правильных многогранников, можно встретить во многих работах Эшера. Наиболее интересной среди них является гравюра «Звезды» на которой можно увидеть тела, полученные объединением тетраэдров, кубов и октаэдров. Помещенный внутрь центральной фигуры хамелеон затрудняет общее восприятие. Этот аспект данной картины является еще одним предметом восхищения математиков творчеством Эшера.
Слайд 30
Правильные многогранники в архитектуре
Платоновы тела или правильные многогранники
в архитектуре в чистом виде встречаются также крайне редко.
И это в основном гексаэдры.
Слайд 31
Тест «Выбери правильный ответ»
1. Многогранник, составленный из четырех
правильных многоугольников:
А) Тетраэдр В) Куб
С) Октаэдр D) Икосаэдр Е) Додекаэдр
2. Многогранник, каждая вершина которого является вершиной трех квадратов:
А) Тетраэдр В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэдр
3. Многогранник, каждая вершина которого является вершиной пяти треугольников:
А) Тетраэдр В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэдр
4. Многогранник, с восьмью гранями:
А) Тетраэдр В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэдр
5. Многогранник, составленный из пятиугольников:
А) Тетраэдр В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэдр
Слайд 32
Узнай фигуру
1.Тетраэдр
2.Куб
3.Октаэдр
4.Икосаэдр
5.Додекаэдр
Слайд 33
Книги по созданию многогранников
Слайд 35
Ответы на тест
1А
2В
3Д
4 С
5Е
Узнай фигуру: 1-куб, 2-октаэдр,3-додекаэдр