расстояние от точки отсчета в метрах, t — время в
секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 9 с.Задача №1
Ответ: 60 м/с.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть







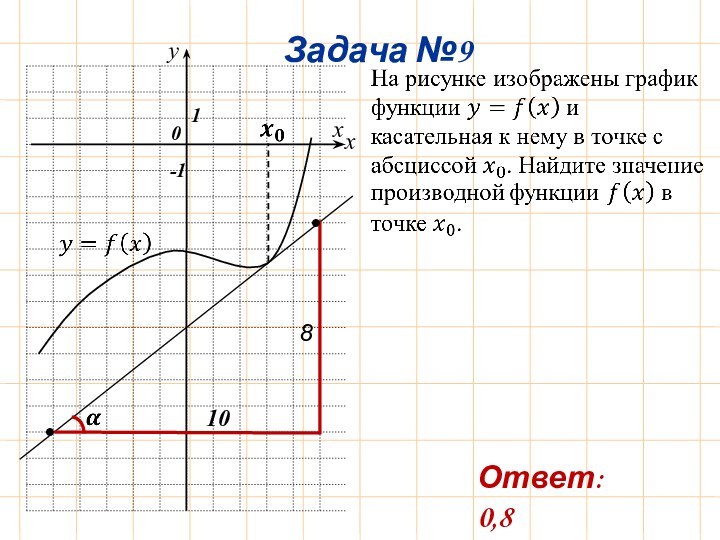
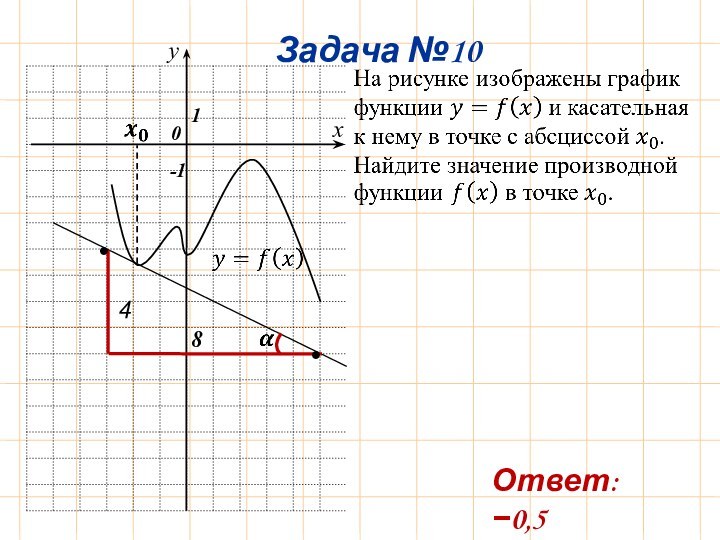
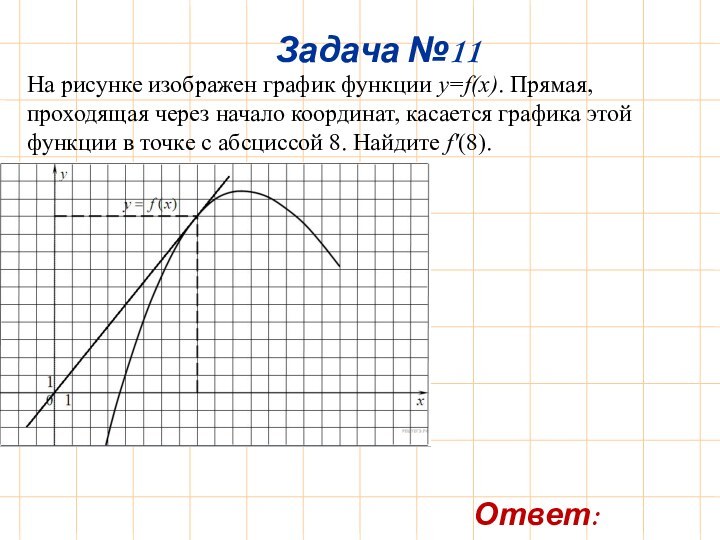
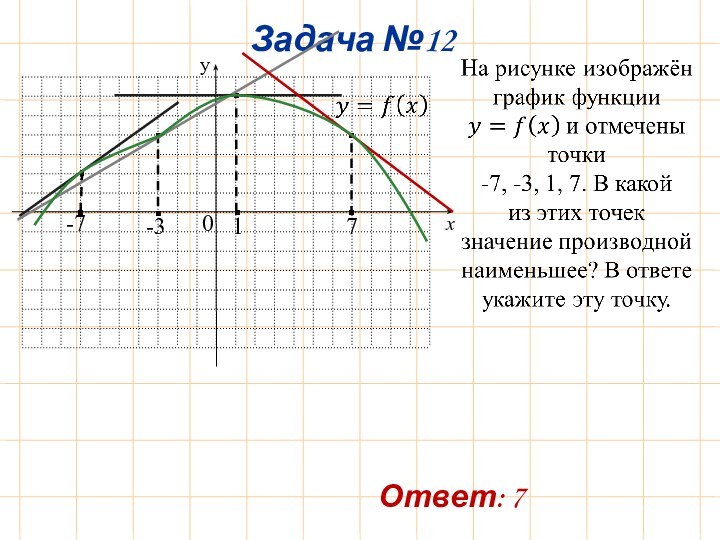
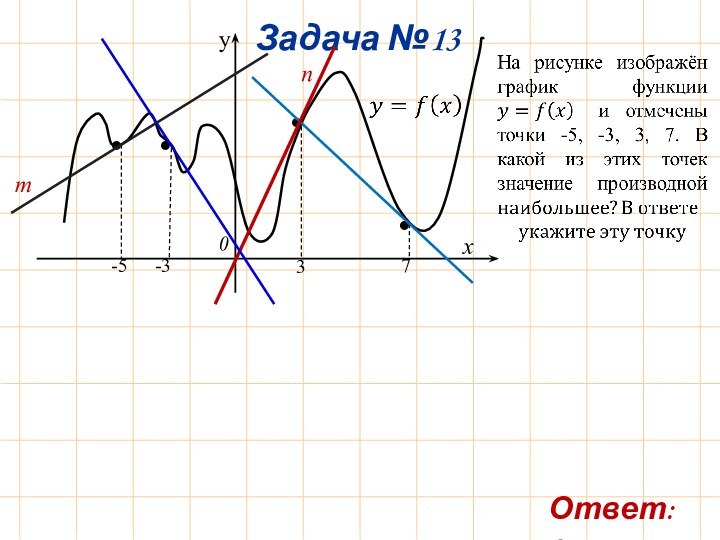

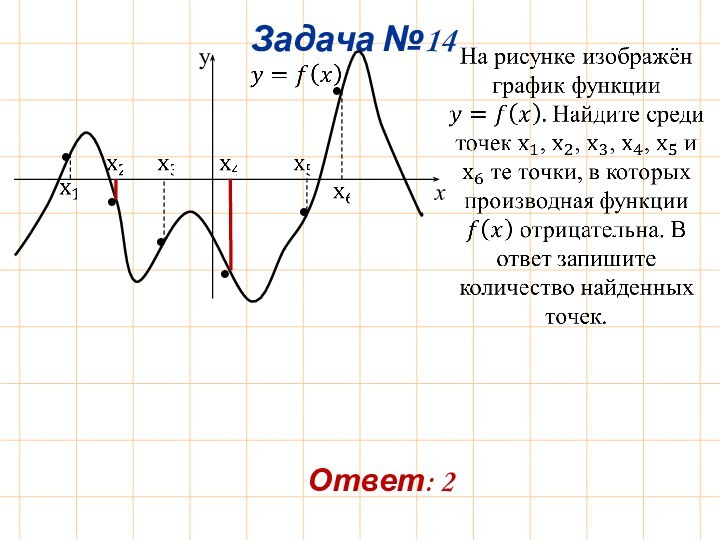
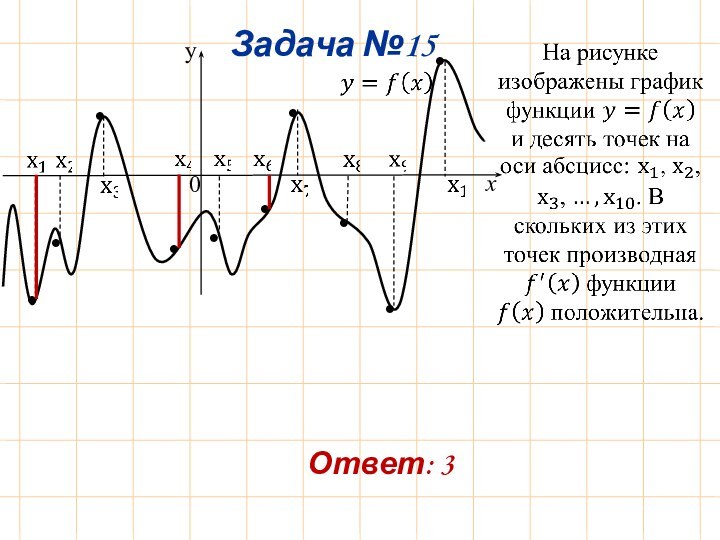
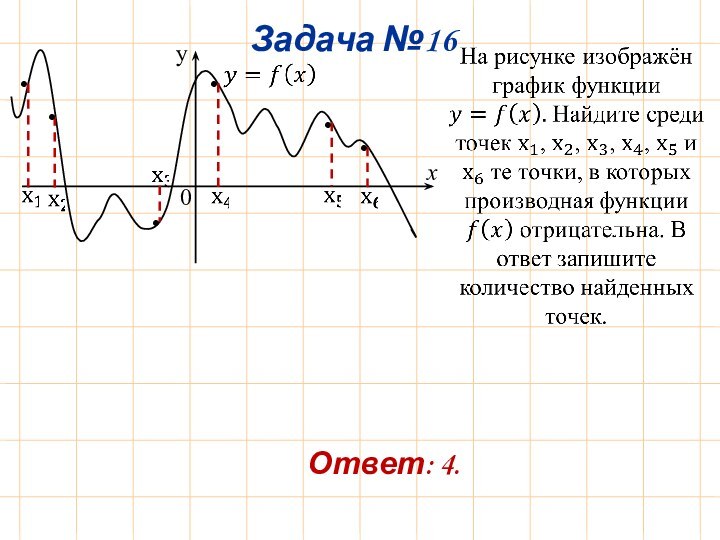





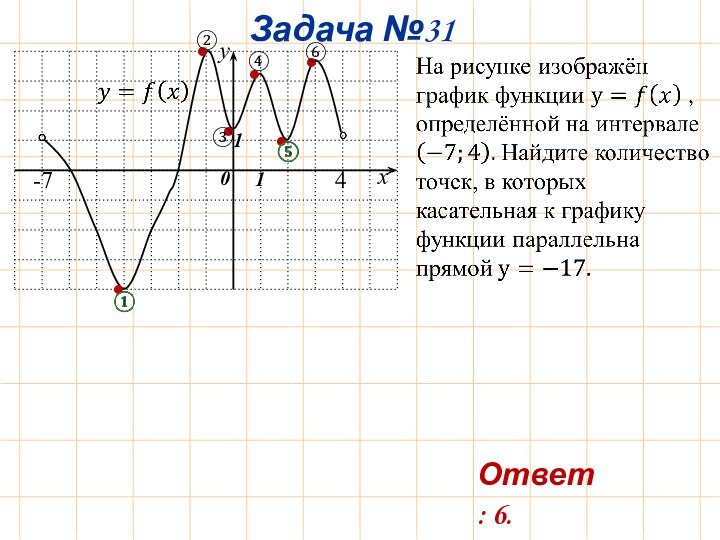
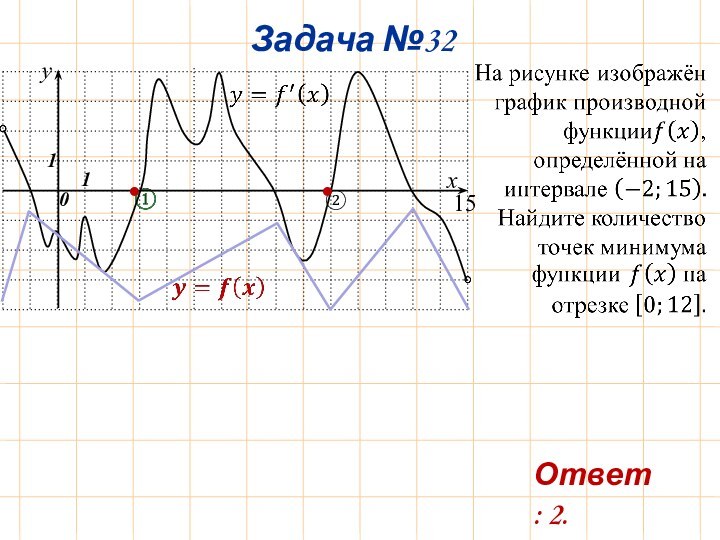
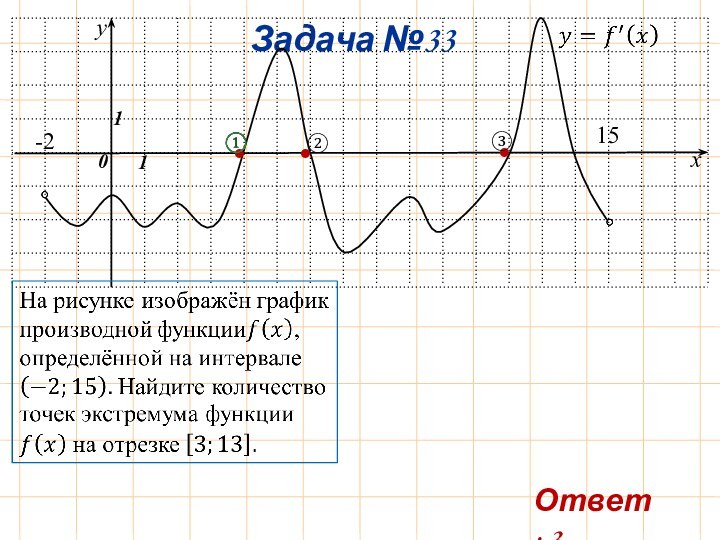
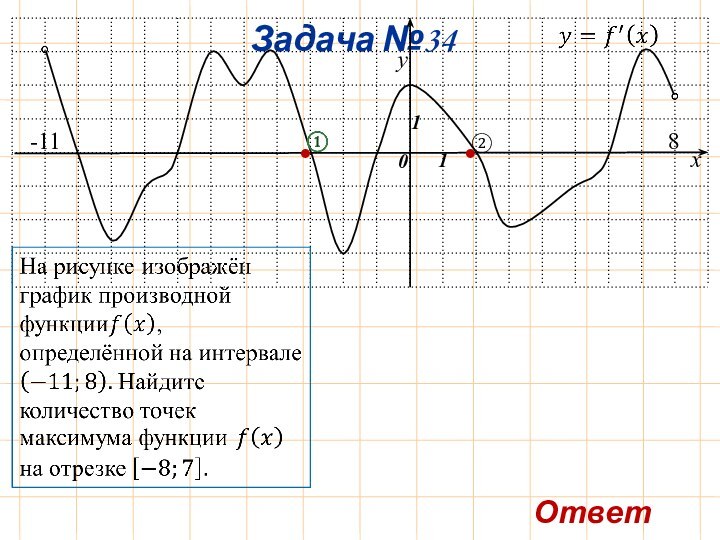


Задача №1
Ответ: 60 м/с.
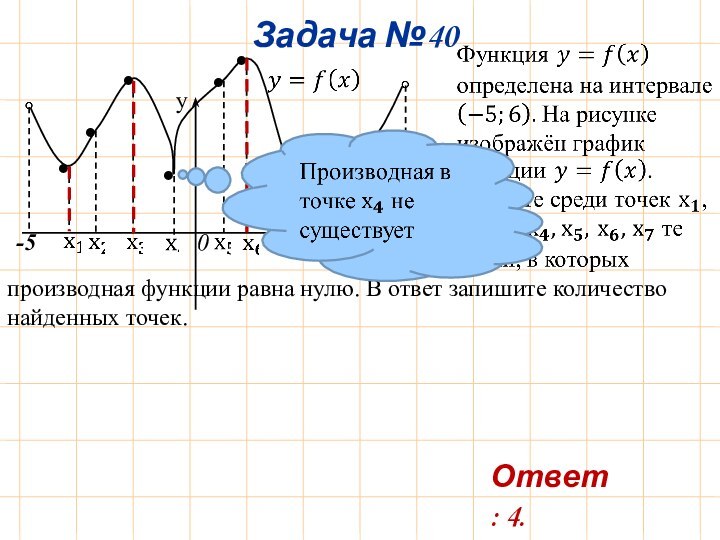
Задача №2
Ответ: 20 м/с.
Задача №3
Ответ: 59 м/с.
Задача №4
Ответ: 7с.
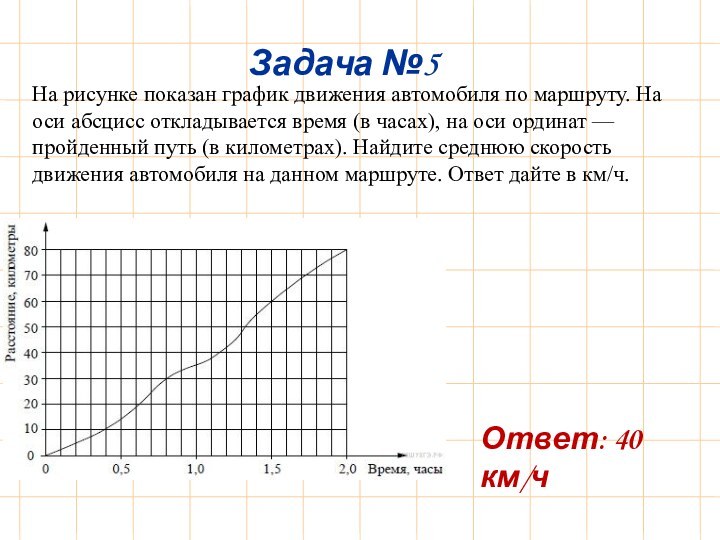
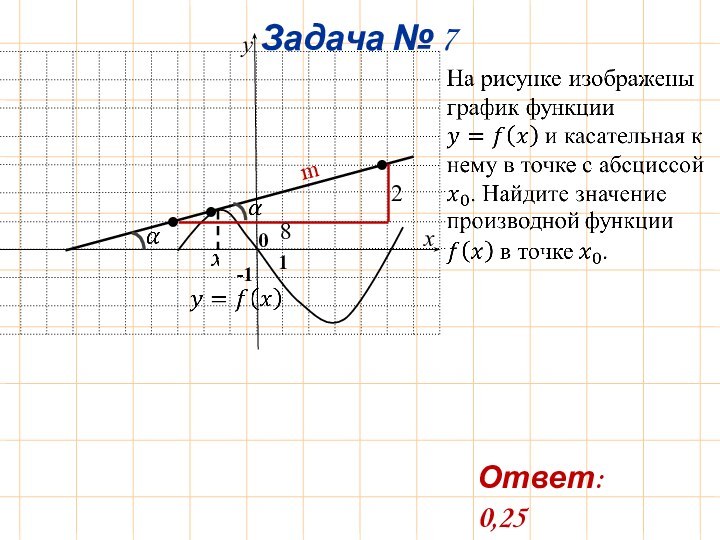
Ответ: 40 км/ч
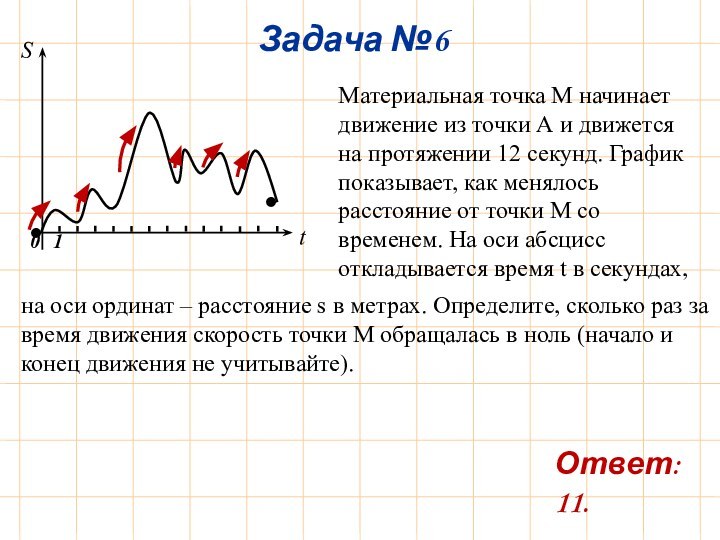
на оси ординат – расстояние s в метрах. Определите, сколько раз за время движения скорость точки М обращалась в ноль (начало и конец движения не учитывайте).
Ответ: 11.
Задача №11
Ответ: 1,25
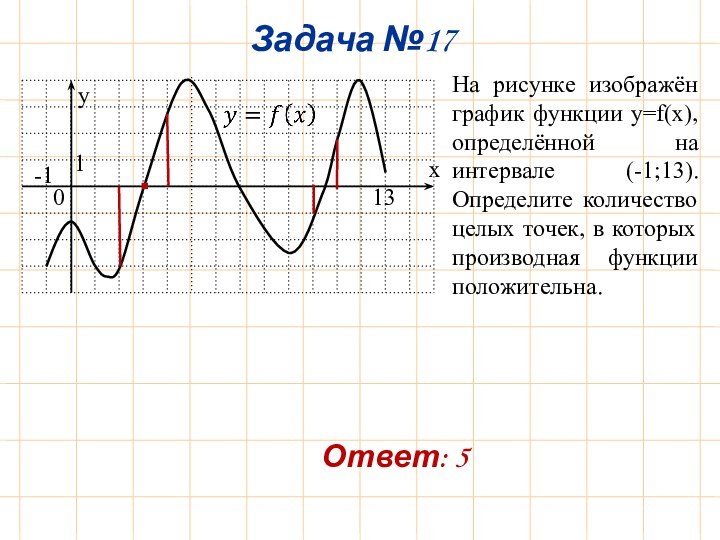
Ответ: 5
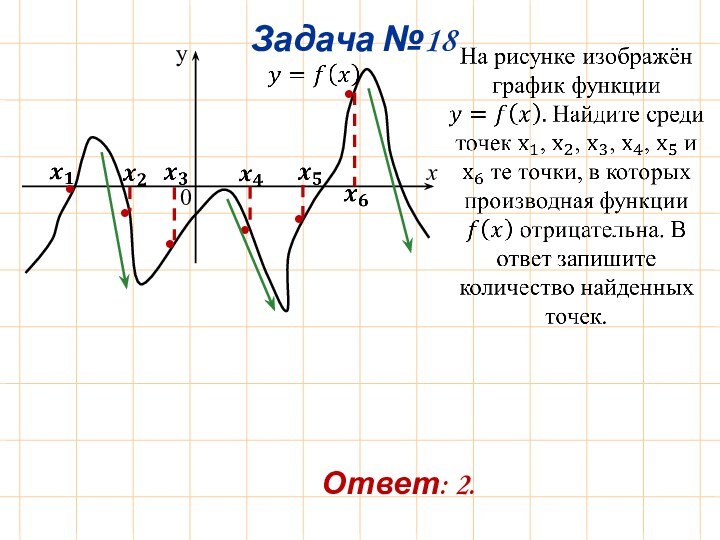
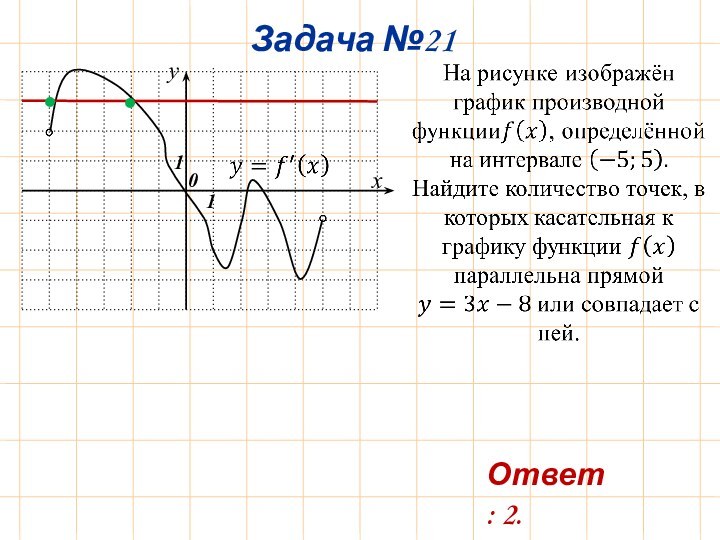
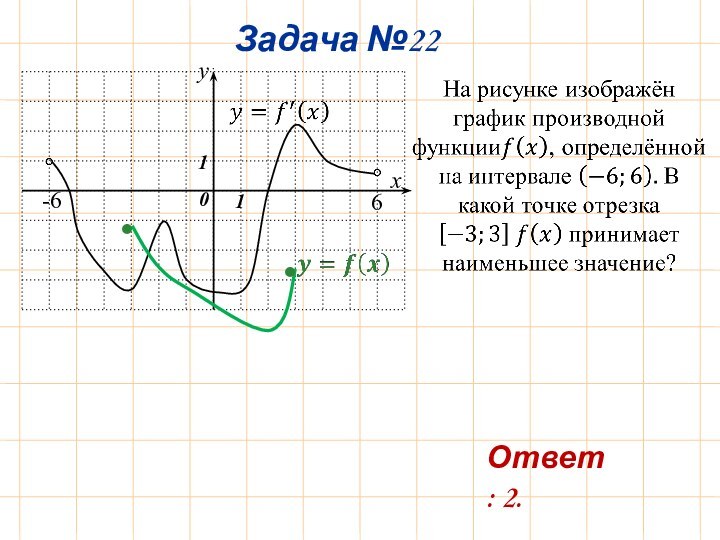
Ответ: 2.
Прямая y = − 4x − 8 является касательной к графику функции
y = x3 − 3x2 − x − 9. Найдите абсциссу точки касания.
Задача №27
Решение.
Значение производной функции в точке касания
равно угловому коэффициенту касательной, т. е. y / = 3
y / = 3 x2 + 8x + 3
3 x2 + 8x + 3 = 3
x(3x+8) = 0. Отсюда x = 0 или x = 8/3
Уравнению x3 + 4x2 + 3x + 4 = 3x + 4 удовлетворяет только
x = 0. Значит, абсцисса точки касания равна 0, а тогда ее
ордината равна 4.
Ответ: 4.
Задача №28
Решение.
Ответ: 0,125.
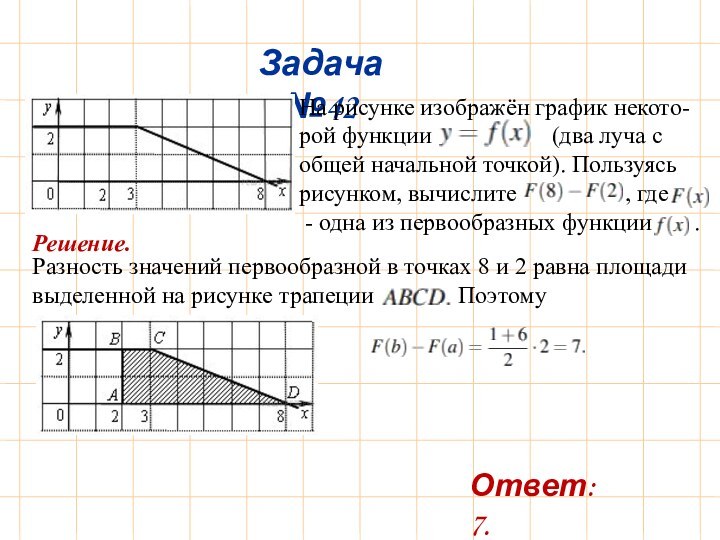
Задача №29
Решение.
График заданной функции − парабола. Касательная к параболе
имеет с ней единственную общую точку. Поэтому необходимо и достаточно, чтобы уравнение 3x2 − 3x + с = 3x + 4 имело единственно решение. Получим
3x2 − 6x + с − 4 = 0
D = 36 − 12(с − 4) = 36 − 12с+ 48 = 84 − 12с
Для этого дискриминант должен быть равен нулю, откуда
84 − 12с = 0
с = 84/12 = 7
Ответ: 7.