- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Производные. Механический, физический, геометрический и экономический смысл производных
Содержание
- 2. ОПРЕДЕЛЕНИЕПроизво́дная (функции в точке) — основное понятие дифференциального
- 3. ПРИМЕР РЕШЕНИЯ
- 4. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ Производной функции y = f(x) в точке
- 5. ПРИМЕР РЕШЕНИЯПроизводная в точке x0 равна угловому коэффициенту
- 6. ФИЗИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ.Если точка движется вдоль оси
- 7. ЭКОНОМИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ Производительность труда есть производная объема продукции по времени.
- 8. ПРИМЕР РЕШЕНИЯ
- 9. Скачать презентацию
- 10. Похожие презентации
ОПРЕДЕЛЕНИЕПроизво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует.








Слайд 4
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
Производной функции y = f(x) в точке Х
называется предел, если он существует, отношения приращения функции к
приращению аргумента при стремлении последнего к нулю. 2. геометрически – как угловой коэффициент касательной к графику функции в этой точке.
Слайд 5
ПРИМЕР РЕШЕНИЯ
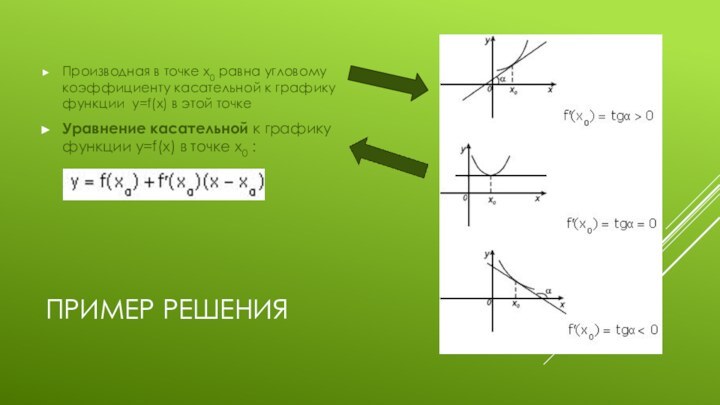
Производная в точке x0 равна угловому коэффициенту касательной
к графику функции y=f(x) в этой точке
Уравнение касательной к графику
функции y=f(x) в точке x0 :





























