Слайд 2
Цели урока :
Познакомить учащихся с тем , что
изучает геометрия, какой раздел геометрии называется планиметрией, какие фигуры
в планиметрии называют основными ; систематизировать сведения о взаимном расположении точек и прямых ;
рассмотреть свойство прямой : через любые две точки можно провести прямую, и притом только одну;
научить обозначать точки и прямые на рисунке ;
ввести понятие отрезка;
рассказать о практическом проведении (провешивании) прямых на местности.
Слайд 3
Возникновение и развитие геометрии.
Геометрия возникла в результате практической
деятельности людей :
нужно было сооружать жилища, храмы, прокладывать
дороги, оросительные каналы, устанавливать границы земельных участков и определять их размеры.
В
переводе с древнегреческого слово «геометрия» означает «земледелие» ( « гео» -земля , а «метро»- мерить).
Важную роль играли и эстетические потребности людей : желание украсить свои жилища и одежду, рисовать картины окружающей жизни. Все это способствовало формированию и накоплению геометрических сведений.
Слайд 5
За несколько столетий до нашей
эры в Вавилоне, Китае, Египте и Греции уже существовали
начальные геометрические знания, которые добывались в основном опытным путем, но они не были еще систематизированы и передавались от поколения к поколению в виде правил и рецептов, например, правил нахождения площадей фигур, объемов тел, построения прямых углов и т. д.
Не было еще доказательств этих правил, и их изложение не представляло собой научной теории.
Слайд 6
Первым ,кто начал получать геометрические факты
при помощи рас -суждений (доказательств),
был древнегреческий ма -тематик Фалес
(VI в.до н.э.), который в своих исследованиях применял перегибание чертежа, поворот части фигуры и так далее, то есть то, что на современном языке называется движением.
Слайд 7
Постепенно геометрия становится наукой, в которой
большинство фактов устанавливается путем выводов, рассуждений, доказательств.
Попытки греческих
ученых привести геометрические факты в систему начинаются уже в V веке до н.э. Наибольшее влияние на всё последующее развитие геометрии оказали труды греческого ученого Евклида, жившего в Александрии в III веке до н.э.
Слайд 8
Сочинение Евклида «Начала» почти 2000 лет служило основной
книгой , по которой изучали геометрию .
В «Началах»
были систематизированы известные к тому времени геометрические сведения, и геометрия впервые предстала как математическая наука.
Эта книга была переведена на языки многих народов мира , а сама геометрия, изложенная в ней, стала называться евклидовой геометрией.
Слайд 9
Что изучает геометрия?
В геометрии изучаются формы, размеры,
взаимное расположение предметов независимо от их других свойств :
массы, цвета и т.д.
Отвлекаясь от этих свойств и беря во внимание только форму и размеры предметов, мы приходим к понятию геометрической фигуры.
Слайд 10
Геометрия не только дает представление о
фигурах, их свойствах, взаимном расположении, но и учит рассуждать
, ставить вопросы, анализировать , делать выводы , то есть логически мыслить.
Слайд 11
Школьный курс геометрии делится на :
планиметрию
стереометрию
Планиметрия – это
раздел геометрии, изучающий свойства фигур на плоскости
( от
латинского слова «платинум» - плоскость и греческого «метрио» - измеряю).
Примеры плоских фигур : отрезок , луч , прямая, угол, окружность, круг, треугольник, прямоугольник .
Стереометрия – это раздел геометрии, который изучает свойства фигур в пространстве.
Примеры объёмных фигур : параллелепипед, шар, цилиндр, пирамида , конус…
Слайд 12
Вам уже знакомы некоторые геометрические фигуры
.
точка
прямая
отрезок
луч
угол
треугольник
прямоугольник
круг
Слайд 13
Примеры объёмных фигур.
куб
шар
конус
цилиндр
пирамида
Слайд 14
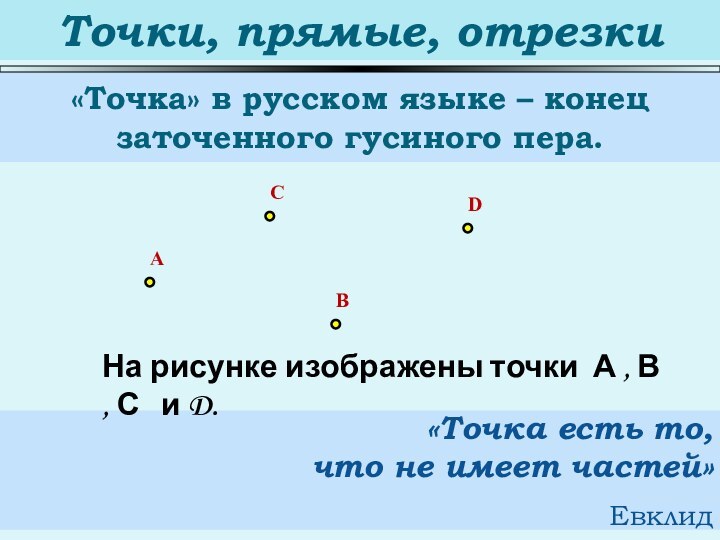
Точки, прямые, отрезки
«Точка» в русском языке – конец
заточенного гусиного пера.
A
C
B
D
«Точка есть то,
что не имеет частей»
Евклид
На рисунке
изображены точки А , В , С и D.
Слайд 15
Точки, прямые, отрезки
Прямая – множество точек, построенных с
помощью линейки.
Слайд 16
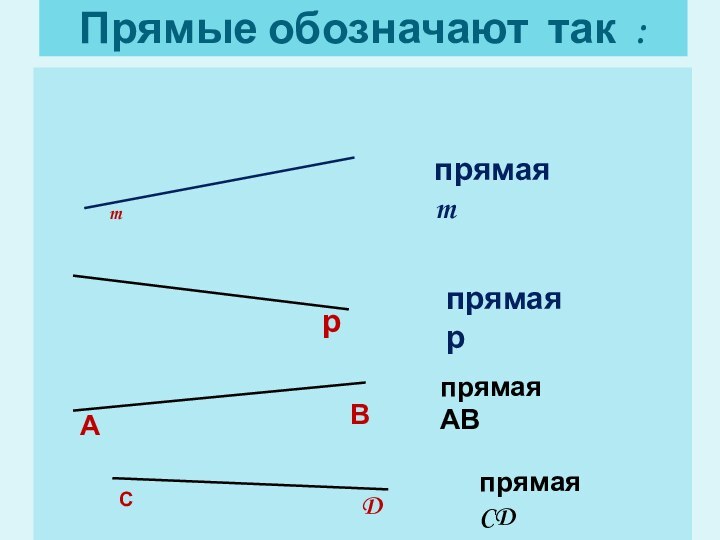
Прямые обозначают так :
m
прямая m
р
прямая р
А
В
прямая АВ
С
D
прямая
Слайд 17
Точки, прямые, отрезки
Через любые две точки можно провести
прямую,
и притом только одну.
c
Две прямые либо имеют только
одну общую точку, либо не имеют общих точек.
.
.
d
Слайд 18
Точки, прямые, отрезки
Отрезок – часть прямой, ограниченная двумя
точками. Точки A и B – концы отрезка
A
B
Отрезок с
концами А и В обозначают АВ или ВА.
Он содержит точки А и В и все точки прямой, лежащие между точками А и В.
Слайд 19
Практическое задание.
Задания № 1 , 2 , 3
стр. 7
Слайд 20
Ответьте на вопросы:
1. Можно ли через данную точку
провести прямую?
2. Сколько прямых можно провести через данную точку?
3.
Сколько прямых можно провести через две данные точки?
4. Сколько общих точек могут иметь две прямые?
Слайд 21
Ответьте на вопросы
5. Могут ли прямые ОА и
АВ быть различными , если точка О лежит на
прямой АВ?
6. Даны две прямые а и в , пересекающиеся в точке С , и точка D , отличная от точки С и лежащая на прямой а. Может ли точка Д лежать на прямой в ?
Слайд 22
Выполните самостоятельно :
Задание № 5 стр. 7
Слайд 23
Самостоятельная работа с учебником .
1. Прочитайте п. 2
стр. 6-7.
2. В чём заключается приём «провешивания прямой» и
когда он применяется?
Слайд 24
Математический диктант.
1.Начертите прямую и обозначьте её буквой в.
а) Отметьте точку М ,лежащую на прямой
в.
б) Отметьте точку Д , не лежащую на прямой в.
в) Используя символы , запишите предложение : «Точка М лежит на прямой в , а точка Д не лежит на ней».
2. Начертите прямые а и в , пересекающиеся в точке К. На прямой а отметьте точку С , отличную от точки К.
а) Являются ли прямые КС и а различными прямыми ? Ответ обоснуйте.
б) Может ли прямая в проходить через точку С? Ответ обоснуйте.
Слайд 25
Итоги урока.
Задайте вопросы своим одноклассникам по содержанию
сегодняшнего урока.
Слайд 26
Есть вопросы…
Непонятно!
Всё понятно!
Пункты 1 и2 ,
ответить
на вопросы
1-3 на стр. 25 учебника
Задания №
4, 6 , 7.