Евклида до Лобачевского»
2.1. «Начала» Евклида
2.2. Пятый постулат 2.3. Гений из Казани
2.4. Модели новой геометрии
2.5. Значение геометрии Лобачевского
3. Заключение
4. Список литературы
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть














По «Началам» можно судить, что Евклид был не только хорошим математиком, но и замечательным педагогом.
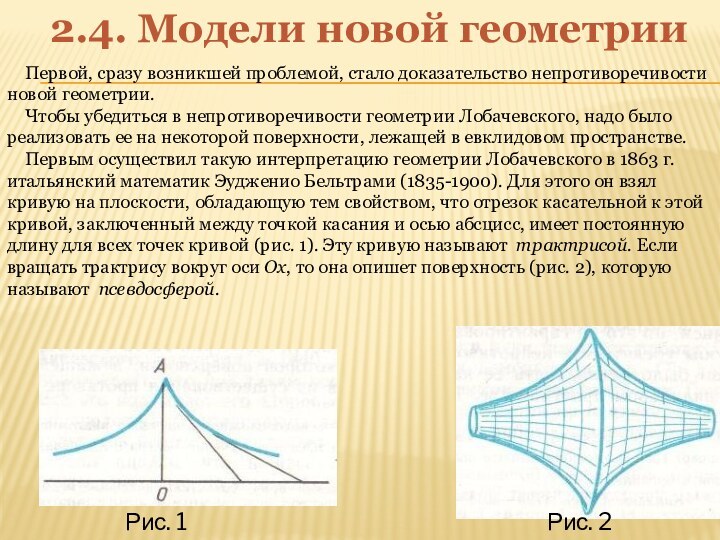
Рис. 1
Рис. 2
Рис. 1
Рис. 3