- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему ЗАМАСКИРОВАННЫЕ УСЛОВИЕМ КОМБИНАТОРНЫЕ ЗАДАЧИ
Содержание
- 2. Задача №1Властелин зла обосновался на планете Гуано.
- 3. Решение задачи №1Посчитаем, сколько лет Властелин Зла
- 4. Задача №2На доске 8*8 расставлено 8 красных
- 5. Решение задачи №2Количество способов расставить красные фишки
- 6. Задача №3На столе лежит 36 шариков. Кощей
- 7. Решение задачи №3Задача сводится к нахождению количества
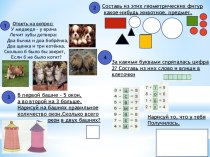
- 8. Задача №435 малышей в детском саду строят
- 9. Скачать презентацию
- 10. Похожие презентации
Задача №1Властелин зла обосновался на планете Гуано. После очередного передела мира он забавляется так: на своей трёхмерной карте планеты он перекрашивает 6 государств в 6 различных цветов. Каждое перекрашивание занимает у него один гуанский месяц, при









Слайд 3
Решение задачи №1
Посчитаем, сколько лет Властелин Зла будет
занят перекрашиванием карты.
6!/12=5!/2=60 лет.
Теперь найдём, сколько лет пройдёт,
пока все государства договорятся о мире. Каждое из 6 государств должно заключить договор с 5 государствами, а всего договоров 6*5/2=15.
Государствам на Гуано требуется 15*5=75 лет при времени переговоров 5 лет (и тогда начнётся новая война) и 15*4 = 60 лет при времени переговоров 4 года, что даёт надежду изгнать Властелина Зла.
Слайд 4
Задача №2
На доске 8*8 расставлено 8 красных фишек
так, что никакие две не лежат на одной горизонтали
или вертикали. На эту доску поставили наибольшее количество зелёных фишек так, чтобы никакие две зелёные и две красные фишки не находились в вершинах прямоугольника, стороны которого параллельны сторонам доски. Сколькими способами это можно сделать?
Слайд 5
Решение задачи №2
Количество способов расставить красные фишки –
8!, и для каждого из них 2^28 – количество
способов расставить 28(максимальное количество) зелёных фишек.Основная идея: каждая пара красных является вершинами ровно одного прямоугольника, таких прямоугольников 28, и каждая свободная клетка доски является угловой ровно для одного прямоугольника.
Значит в каждом таком прямоугольнике нужно поставить зелёную фишку ровно на одну из двух угловых клеток, что можно сделать двумя способами.
Ответ: 8!*2^28.
Слайд 6
Задача №3
На столе лежит 36 шариков. Кощей и
Василиса Премудрая играют в игру. Каждый из них по
очереди разбивает шарики на группы (может быть, на одну), в каждой из которой равное число шариков. Число групп не может повторяться. Проигрывает тот, кто не сможет найти новое разбиение.Кто выигрывает, если начал игру Кощей?
Слайд 7
Решение задачи №3
Задача сводится к нахождению количества различных
делителей числа 36.
Разложим его на простые множители: 36=2^2*3^2. Число
делителей равно (2+1)*(2+1)=9. это число нечётное, значит закончит игру тот, кто её начинал.Выиграет кощей.