Презентация на тему Развитие понятия о числе

изучения темы студент должен уметь выполнять преобразования с действительными

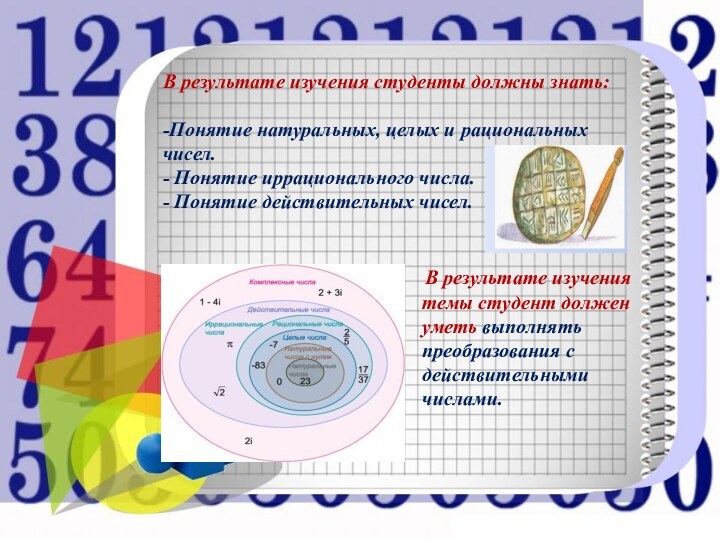
числами.

В результате изучения студенты должны знать:

-Понятие натуральных, целых и рациональных чисел.
- Понятие иррационального числа.
- Понятие действительных чисел.

потребностей счета, понятие числа с развитием науки значительно расширилось.

.

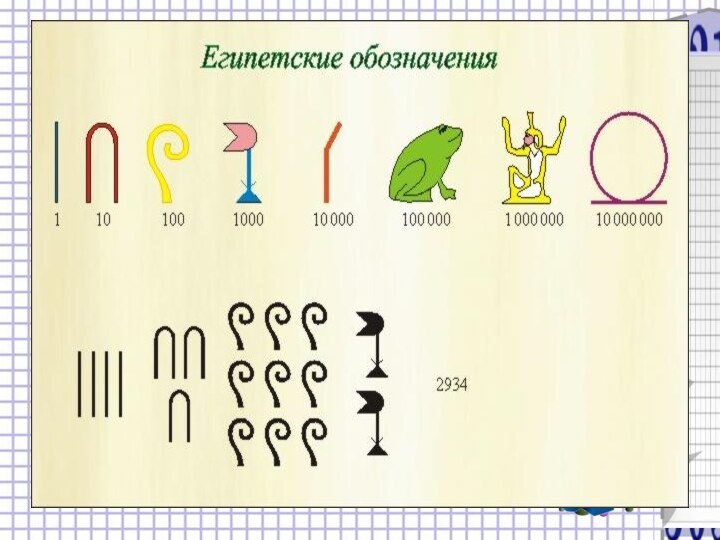
На первых этапах существования человеческого общества числа, открытые в процессе человеческой деятельности, служили для примитивного счета предметов, дней, шагов и т.п.

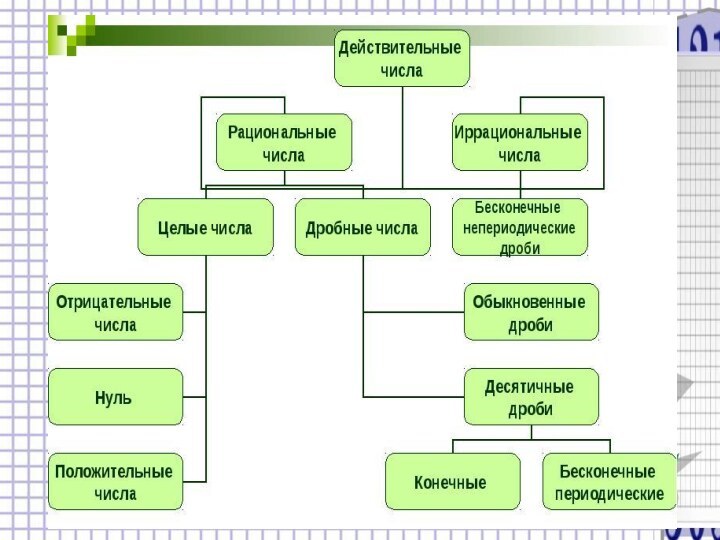
Число- основное понятие математики, используемое для количественной характеристики, сравнения, нумерации объектов и их частей. Письменными знаками для обозначения чисел служат цифры, а также символы математических операций.

В связи с решением уравнений математики встречались с числом,

которое выражалось

С развитием цивилизации ему потребовалось изобретать все большие и большие числа, уметь их записывать. Этот процесс продолжался на протяжении многих столетий и потребовал напряженного интеллектуального труда
Потребовалась не одна сотня лет для того, чтобы математики смогли осмыслить понятие иррационального числа, и выработать способ записи такого числа и приближенного значения его в виде бесконечной десятичной дроби.

.Оно получило название мнимой единицы. После того как норвежский математик Гаспар Вессель (1745-1818) нашел возможность представить мнимое число геометрически, то так называемые «мнимые числа» получили свое место в множестве комплексных чисел.

В связи с решением уравнений математики встречались с числом,

которое выражалось

.

Первая дробь, с которой познакомились люди, была, наверное, половина. За ней последовали ¼, 1/8, …, затем 1/3, 1/6 и т.д., то есть самые простые дроби, у них числитель всегда единица. Лишь значительно позже у греков, затем у индейцев и других народов стали входить в употребление и дроби общего вида, называемые обыкновенными, у которых числитель и знаменатель могут быть любыми натуральными числами. В дальнейшем оказалось необходимым еще более расширить понятие числа. Последовательно появились числа иррациональные, отрицательные и комплексные.

В связи с решением уравнений математики встречались с числом,

которое выражалось

.

Довольно поздно к семье чисел присоединился нуль. Первоначально слово нуль означало отсутствие числа(буквальный смысл латинского слова nullum –“ничего»). Действительно, если, например, от 3 отнять 3, тоне останется ничего. Для того, чтобы это «ничего» считать числом, появились основания лишь в связи с рассмотрением отрицательных чисел.
http://ppt-online.org/18501

естественным образом при счёте (как в смысле перечисления, так

и в смысле исчисления).
Множество всех натуральных чисел принято обозначать знаком N. Множество натуральных чисел является бесконечным, так как для любого натурального числа найдётся большее его натуральное число.

выводящим результат из множества натуральных чисел) над натуральными числами

относятся следующие арифметические операции:
Сложение. Слагаемое + Слагаемое = Сумма
Умножение. Множитель * Множитель = Произведение
Возведение в степень , ab где a — основание степени и b — показатель степени. Если основание и показатель натуральны, то и результат будет являться натуральным числом.
Дополнительно рассматривают ещё две операции. С формальной точки зрения они не являются операциями над натуральными числами, так как не определены для всех пар чисел (иногда существуют, иногда нет).
Вычитание. Уменьшаемое Вычитаемое = Разность. При этом Уменьшаемое должно быть больше Вычитаемого (или равно ему, если считать 0 натуральным числом).
Деление. Делимое / Делитель = (Частное, Остаток).

целых чисел образует множество целых чисел. Число вида а/в,

где а и b целые числа, причём

называется рациональным числом. Множество, состоящее из положительных и отрицательных дробных чисел, называется множеством рациональных чисел.

A.B=B.A
Ассоциативность сложения. (A+B)+C=A+(B+C)
Ассоциативность умножения. (AB)C=A(BC)
Дистрибутивность

умножения относительно
сложения.

= 323
y = 108
z = 749
n = 6
x =

9

a = 349

y = 117

z = 837

Проверьте себя:

виде конечной десятичной дроби, либо в виде бесконечной периодической

десятичной дроби.

Выполнить действия:

1.

2.

Чистой периодической называется дробь, у которой период сразу после

запятой.

.
Смешанной называется дробь, у которой между запятой и первым периодом есть одна или несколько повторяющихся цифр:

.

142857)

периодической дроби в обыкновенную:

Чтобы обратить смешанную периодическую дробь достаточно из числа стоящего до второго периода вычесть число стоящее до первого периода, и полученную разность взять числителем , а знаменателем написать цифру в периоде столькими нулями сколько цифр между запятой и периодом:

такое, что i²=-1

Запись комплексного числа в общем виде

А + В i

А и В - действительные числа А - действительная часть
В - мнимая часть
i - мнимая единица

Термин «комплексные числа» ввел немецкий математик Карл Гаус.

В i
Комплексные числа называются взаимно сопряженными, если их действительные

части равны, а мнимые отличаются знаками

А + В i
Z = A + B i

2)Какие числа называются

целыми? 3)Какие числа называются иррациональными? 4)Докажите, что 5-рациональное число.

II вариант 1) Приведите пример рационального числа. 2)Какие числа называются рациональными? 3) Какие числа называются действительными? 4)Докажите, что -2/5 действительное число.