- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Решение уравнений n-й степени, n>2. Нахождение корней многочленов
Содержание
- 2. Уравнение вида а nх n +а n–1х n–1+…+а¹х+аº=0называется алгебраическим уравнением n-й степени
- 3. Пусть несократимая дробь р/ q является корнем
- 4. Свойство № 2 Если число а –
- 5. Задача 1Решить уравнение: х4+х³+3х²-5х =0 Делители
- 6. 3х4+х³+3х²-5х-2х – 13 х³3х4-3х³4х³+3х²+4х²4х³-4х²+7х7х²-5х7х²-7х+22х-22х-20Задача 1
- 7. 3 х³+4х²+7х+2Возможные корни: ±1, ±⅔, ±⅓, ±2-
- 8. Уравнения высоких степенейМетоды
- 9. Задача 2Решить уравнение (х+1)² (х²+2х)=12(х²+2х(х²+2х)+1)=12(ууу²+у=12у²+у–12 =0х²+2х=у =
- 10. Уравнения специального видаУравнения вида (х-а)(х-b)(х-с)(х-d)=Аа < b < c < d,b-a=d-сХ - У=(а+b+с+d) 4
- 11. Задача 3Решить уравнение(12х–1)(6х –1)(4х – 1)(3х –1)=5(12х–1)(6х
- 12. Задача 3У= 1 12 1614134=—+
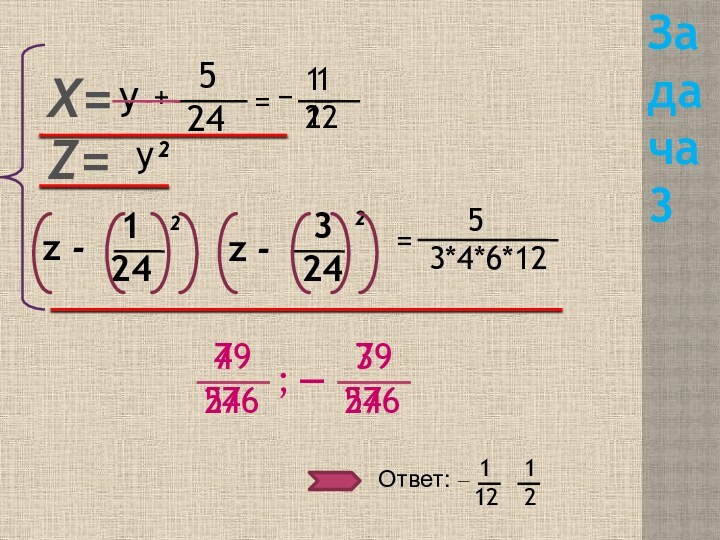
- 13. Z= у²Задача 3Х=z - 124²z - 324²=
- 14. Уравнения вида (х-а)(х-b)(х-с)(х-d)=Ах²аb = сd≠0(х²−(а+b)х+ аb) (х²−(с+d)х+ сd)=Ах²(х²+b1х+с)(х²+b2х+с)=Ax², х² (ах+с/х+ b1)( ах+с/х+ b2)=Аууb1b2
- 15. Задача 4Решить уравнение(х+2)(х+3)(х+8)(х+12)=4х²(х²+14х+24)(х²+11х+24)= 4х². х²у= (у+14)(у+11)=4= -15,
- 16. Скачать презентацию
- 17. Похожие презентации
Уравнение вида а nх n +а n–1х n–1+…+а¹х+аº=0называется алгебраическим уравнением n-й степени





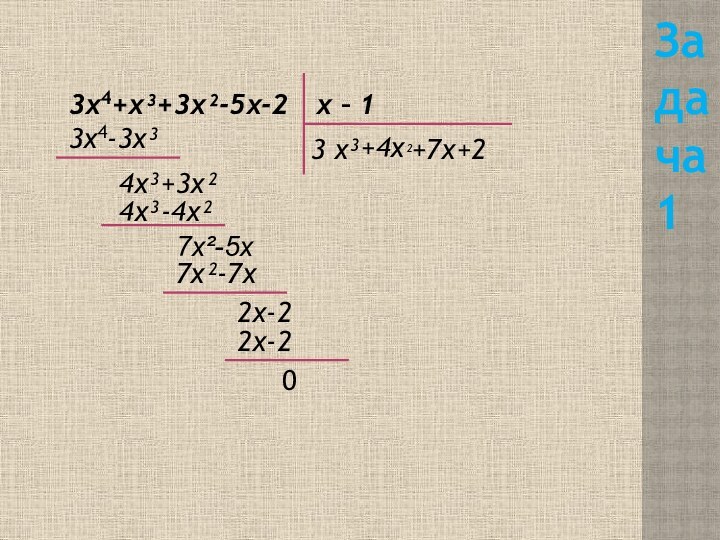




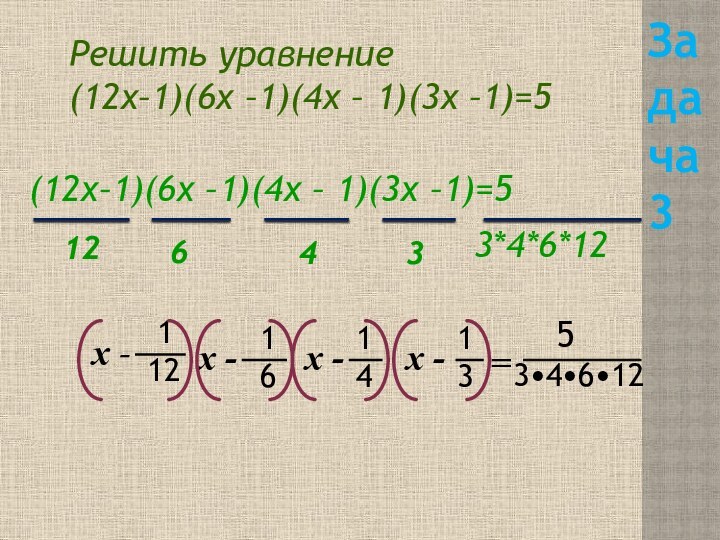
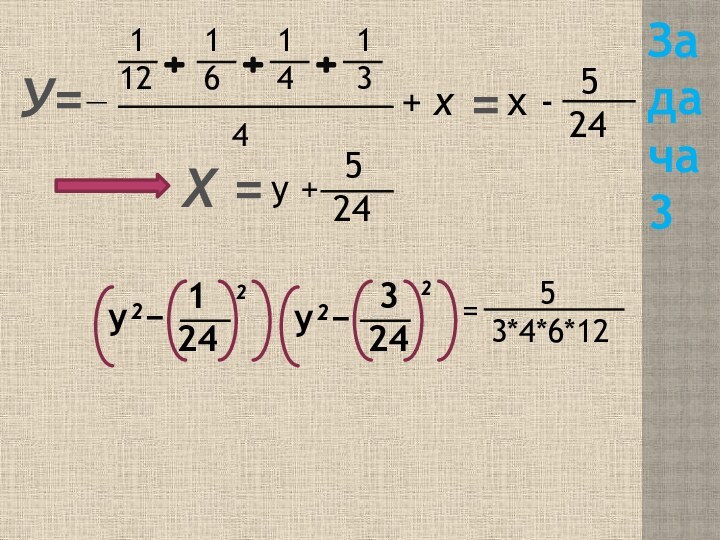



Слайд 3 Пусть несократимая дробь р/ q является корнем многочлена
n-й степени
P(х)= а nх n +а n–1х n–1+…+а¹х+аº
с цельными коэффициентами. Тогда число р является делителем свободного члена а , а q – делителем старшего коэффициентаа nх n +а n–1х n–1+ …+а¹х+аº
q - делитель
Р - делитель
С
в
о
й
с
т
в
о № 1
Слайд 4
С
в
о
й
с
т
в
о
№
2
Если число а – корень
многочлена Р(х), то Р(х) делится на (х – а)
без остатка Р(х)
(х – а)
F(x)
− (х – а)
0
Слайд 5
Задача 1
Решить уравнение: х4+х³+3х²-5х =0
Делители свободного
члена
-2
3
±1,±2
Делители старшего коэффициента
±1, ±3
q
Р
± 1,
±2, ±⅓, ±⅔. Возможные корни уравнения 3* х4+ х³+3* х²−5* х−2=0
1
3*1+1+3*1 – 5*1 – 2 =0
0=0
1 – корень уравнения
1
1
1
Слайд 7
3 х³+4х²+7х+2
Возможные корни: ±1, ±⅔, ±⅓, ±2
- ⅓
- корень уравнения
х +⅓
3х²
3 х³+х²
+3х
3х²+7х
3х²+х
6х+2
+6
6х+2
0
Ответ: 1,
−⅓ Задача 1
Слайд 9
Задача 2
Решить уравнение (х+1)² (х²+2х)=12
(х²+2х
(х²+2х)
+1)
=12
(у
у
у²+у=12
у²+у–12 =0
х²+2х=у
= 3,
= -
4х²+2х
х²+2х
у у
х=1
х= - 3
Ответ: 1; - 3
Корней нет
Слайд 10
Уравнения специального вида
Уравнения вида (х-а)(х-b)(х-с)(х-d)=А
а < b
c < d,
b-a=d-с
Х -
У=
(а+b+с+d)
4
Слайд 11
Задача 3
Решить уравнение
(12х–1)(6х –1)(4х – 1)(3х –1)=5
(12х–1)(6х –1)(4х
– 1)(3х –1)=5
3*4*6*12
12
6
4
3
х -
1
12
х -
1
6
х
- 1
4
х -
1
3
=
5
3•4•6•12
Слайд 13
Z=
у²
Задача 3
Х=
z -
1
24
²
z -
3
24
²
=
5
3*4*6*12
у
5
24
49
576
39
576
;
7
24
724
Ответ:
1
12
1
2
—
+
=
1
2
—
−
1
12
Слайд 14
Уравнения вида (х-а)(х-b)(х-с)(х-d)=Ах²
аb = сd≠0
(х²−(а+b)х+ аb) (х²−(с+d)х+ сd)=Ах²
(х²+b1х+с)(х²+b2х+с)=Ax²,
х²
(ах+с/х+ b1)( ах+с/х+ b2)=А
у
у
b1
b2
Слайд 15
Задача 4
Решить уравнение
(х+2)(х+3)(х+8)(х+12)=4х²
(х²+14х+24)(х²+11х+24)= 4х².
х²
у=
(у+14)(у+11)=4
= -15,
=
- 10
х+24/х
х+24/х
х+24/х
х1 =
–15± √129
2х2 =
−4; −6
(х+24/х
+ 14)
(х+24/х
+ 11)
= 4
у=
у=