Слайд 2
Высказывание в логике является аналогом выражения в арифметике:
В алгебре чисел из чисел при помощи операций +,
-, *, / и (,) можно составлять арифметические выражения.
В логике из простых высказываний (ИСТИНА, ЛОЖЬ) можно составлять логические выражения (составные высказывания) с использованием логических операций.
Слайд 3
Обозначения логических значений
А, В – логические переменные, которые
могут иметь значение ИСТИНА (И), ЛОЖЬ (Л).
А = 2
+ 2 = 4;
В = рыбы живут на суше;
НАПРИМЕР:
Слайд 4
Таблица истинности
- таблица, устанавливающая соответствие между возможными значениями
наборов логических переменных и значениями функции.
Введем обозначения: 0 –
ЛОЖЬ, 1 - ИСТИНА
Слайд 5
Основные логические операции
И – логическое умножение,
ИЛИ – логическое
сложение,
НЕ – логическое отрицание.
Простые высказывания могут быть связаны
между собой словами И, ИЛИ, НЕ. Получившееся высказывание – сложное высказывание.
Слайд 6
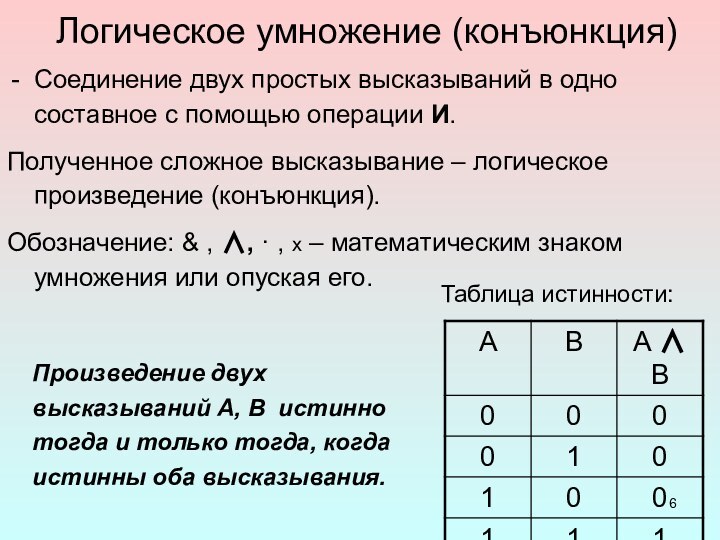
Логическое умножение (конъюнкция)
Соединение двух простых высказываний в одно
составное с помощью операции И.
Полученное сложное высказывание –
логическое произведение (конъюнкция).
Обозначение: & , , · , x – математическим знаком умножения или опуская его.
Таблица истинности:
Произведение двух высказываний А, В истинно тогда и только тогда, когда истинны оба высказывания.
Слайд 7
Например:
«Солнце светит и нет дождя»
Обозначим:
А = «Солнце
светит»,
В = «нет дождя».
С = АВ
С = «Солнце светит и нет дождя».
Слайд 8
Логическое сложение (дизъюнкция)
Союз ИЛИ в обиходе применим в
двух различных значениях:
в исключающем и
неисключающем смысле.
Например:
«Обычно в 8 вечера я смотрю телевизор или пью чай» - союз «или» взят в неисключающем (объединительном) смысле, так как мы можем и смотреть телевизор и одновременно пить чай.
«Данный глагол I или II спряжения» - союз «или» используется в исключающем (разделительном) смысле.
Разъяснение:
Слайд 9
Примеры строгих и нестрогих дизъюнкций:
Слайд 10
Логическое сложение (дизъюнкция)
Соединение двух простых высказываний в одно
составное с помощью операции ИЛИ, употребляемой в неисключающем смысле.
Полученное сложное высказывание – логическая сумма (дизъюнкция).
Обозначается , + .
Таблица истинности:
Сумма двух высказываний А, В истинна тогда и только тогда, когда истинно хотя бы одно высказывание.
Слайд 11
Например:
«Студент едет в электричке или читает книгу»
Обозначим:
А
= «Студент едет в электричке»,
В = «Студент читает книгу».
С = А В
С = «Студент едет в электричке или читает книгу».
Слайд 12
Логическое отрицание (инверсия)
Присоединение частицы НЕ к сказуемому данного
высказывания А, или словосочетания «неверно, что» ко всему высказыванию
Полученное
новое высказывание называется отрицанием высказывания А или логическое отрицание.
Обозначение: ¬A, Ā.
Если А – истинное высказывание, то ¬A – ложное высказывание, и наоборот.
Таблица истинности:
Отрицание истинного высказывания есть ложь.
Слайд 13
Например:
«Число 5 является делителем числа 30»
Обозначим:
А =
«Число 5 является делителем числа 30»,
Ā = «Число 5 НЕ является делителем числа 30».
К = «Некоторые цыплята - кошки»,
К = «Неверно, что некоторые цыплята - кошки».
Д = «Идет дождь»,
Д = «Неверно, что идет дождь».
Слайд 14
При образовании сложных высказываний из простых можно использовать
несколько логических операций.
Приоритет выполнения операций
(если
нет скобок):
I – НЕ,
II – И,
III – ИЛИ.
Слайд 15
Операции инверсия, конъюнкция и дизъюнкция являются основными операциями
алгебры логики и называются булевыми операциями.
Существуют другие логические
операции. Но они могут быть выражены через основные, поэтому их можно назвать функциями.
Слайд 16
Эквивалентность
Обозначение: ~
Логическая связка «ТОГДА И
ТОЛЬКО ТОГДА»
Сложное высказывание А ~ В (А эквивалентно В)
истинно тогда и только тогда, когда и А и В истинны, или когда и А и В – ложны.
A ~ B =А B A В
Определение через основные функции:
Определение через основные функции:
Слайд 17
Например:
А = Площадь квадрата больше единицы,
В = Сторона
квадрата больше единицы.
Их соединение эквивалентностью:
A ~ B = Площадь
квадрата больше единицы тогда и только тогда, когда сторона квадрата больше единицы.
Слайд 18
Исключающее ИЛИ
(строгая дизъюнкция)
Обозначение: АВ Логическая связка
«ЛИБО…, ЛИБО»
Высказывание, соответствующее исключающему или, похоже на дизъюнкцию, но
исключает одновременную истинность обоих высказываний
Строгая дизъюнкция истинна только тогда, когда одно высказывание истинно, а другое ложно.
Определение через основные функции:
A B = А B А В
Слайд 19
Импликация
Обозначение: А → В Логическая связка
«ЕСЛИ..., ТО» (логическое следование одного высказывания из другого)
Импликация А→В
истинна всегда, за исключением случая, когда А истинно, а В ложно.
Определение через основные функции:
A → B =А + B
A → B =А + B
Слайд 20
Например:
А = На улице дождь.
В = Асфальт
мокрый.
A → B = «Если на улице дождь, то
асфальт мокрый».
Тогда,
если идет дождь (А = 1) и асфальт мокрый (В = 1), то это правильно.
Но если вам скажут, что на улице идет дождь (А = 1), а асфальт остается сухим (В = 0), то вы посчитаете это ложью.
А вот когда дождя на улице нет (А = 0), то асфальт может быть и сухим, и мокрым (например, только что проехала поливальная машина).
Слайд 22
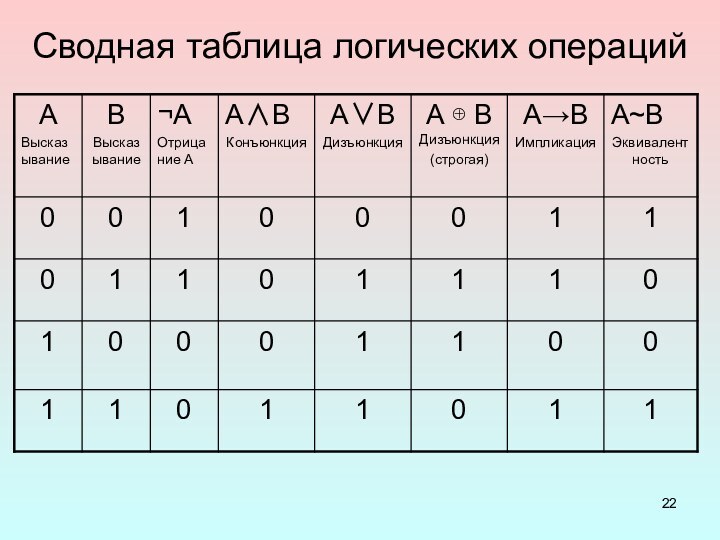
Сводная таблица логических операций
Слайд 23
Приоритет выполнения логических операций
(если нет скобок)
Слайд 24
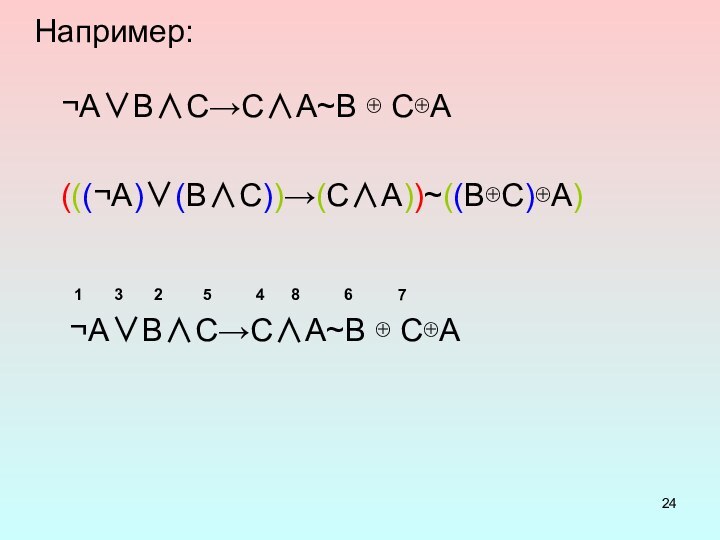
Например:
ABC→CA~B CA
(((A)(BC))→(CA))~((BC)A)
1
3 2
5 4 8 6 7
ABC→CA~B CA
Слайд 25
Перевод логических операций на естественный язык:
Слайд 26
Пример:
Изобразить в виде формулы суждение:
«Я обязательно
поеду на футбольный матч, если достану билет или меня пригласит товарищ и если не будет дождя».
Поездка на стадион зависит от условий:
я достану билет – я не достану билет;
меня пригласит товарищ – меня не пригласит товарищ;
будет дождь –не будет дождя.
Слайд 27
Введем обозначения:
Б – я достану билет;
Б –
я не достану билет;
П – меня пригласит товарищ;
П
– меня не пригласит товарищ;
Д – будет дождь;
Д – не будет дождя.
Слайд 28
Сложное высказывание: «Я достану билет или меня пригласит
товарищ и не будет дождя»
Б ¬Д П
¬Д
или, то же самое –
Б · Д + П · Д
Данное высказывание равносильно поездке на матч – М
М = Б ·¬Д + П ·¬Д
Слайд 29
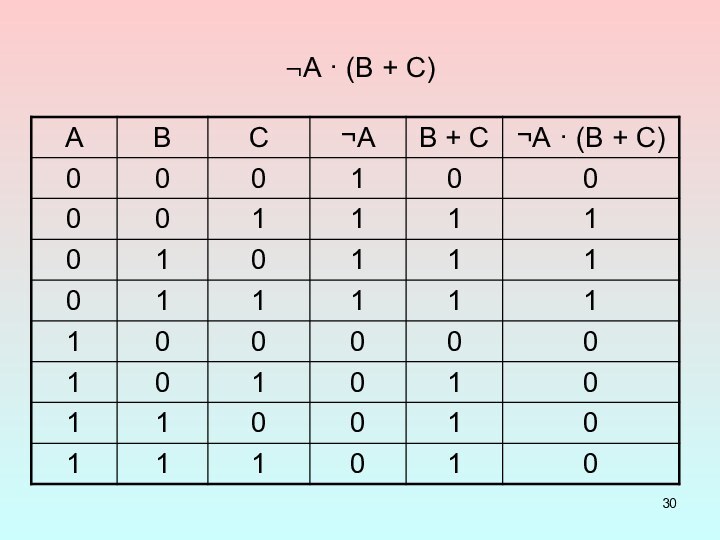
Составление таблицы истинности для сложного высказывания. (Например: А·(В
+ С).)
Правило:
Число исходных столбцов равно числу переменных (простых
высказываний) – n. (в примере n = 3);
Число строк равно 2n. (у нас: 2n = 23 = 8).
Порядок заполнения строк для исходных столбцов:
1-й столбец. Число строк (23 = 8) делится пополам. Верхняя половина заполняется нулями, нижняя – единицами.
2-й столбец. Число строк делится на 4 части. Первая четверть заполняется 0, вторая – 1, третья – снова 0, четвертая 1.
4. В первых строках таблицы выписаны возможные наборы комбинаций значений истинности простых высказываний (А, В, С). В следующих столбцах – значения истинности последовательно выполняемых операций и окончательного результата.
Слайд 31
Самостоятельная работа
1. Составить таблицу истинности:
М = Б ·¬Д
+ П ·¬Д
2. Изобразить в виде формулы:
«Если сегодня будет
хорошая погода, я пойду на прогулку, или буду делать уроки, если погода будет плохая.»
Слайд 32
Доказать справедливость тождества
A + B·C = (A +
B) · (A + C)
Столбцы равны. Тождество доказано.