- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Решето Эратосфена
Содержание
- 2. Одной из самых больших загадок математики является
- 3. (Eratosthenes,
- 4. Книги в то время представляли собой
- 5. В математике Эратосфена интересовал вопрос о том,
- 6. Почему «Решето»?* * *Так как во времена
- 7. Какими бывают числа?Просто́е число́ — это натуральное
- 8. Натуральное числоНатура́льные чи́сла (естественные числа)
- 9. Составное числоСоставное число́ — натуральное число большее 1,
- 10. Как работать с Решетом Эратосфена?Итак, это алгоритм
- 11. Пройдём по ряду чисел, вычёркивая все числа кратные 2(каждое второе)
- 12. Следующее невычеркнутое число 3 –простое.Пройдём по ряду чисел, вычёркивая все числа, кратные 3(каждое третье)
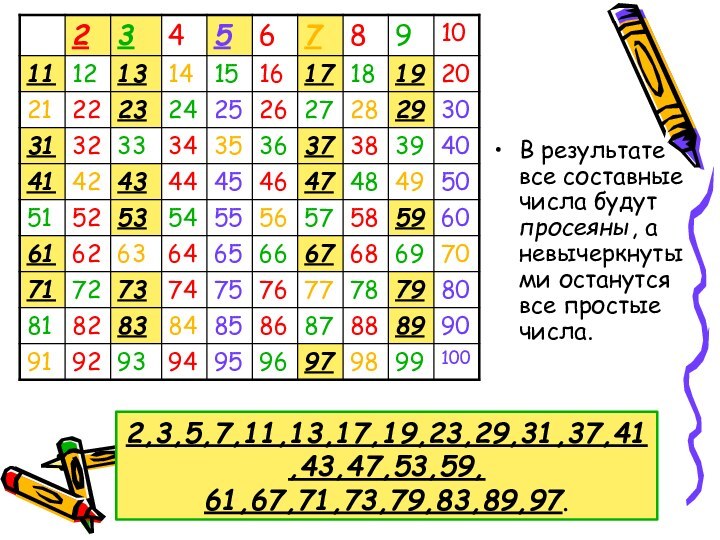
- 13. 3. Следующее невычеркнутое число 5- простое. Пройдём
- 14. 2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59, 61,67,71,73,79,83,89,97.В результате все составные числа будут просеяны, а невычеркнутыми останутся все простые числа.
- 15. Скачать презентацию
- 16. Похожие презентации
Одной из самых больших загадок математики является расположение простых чисел в ряду всех натуральных чисел. Иногда два простых числа идут через одно, (например, 17 и 19, 29 и 31), а иногда подряд идет миллион составных чисел.














Слайд 3
(Eratosthenes, 276-194
г. до н. э.),
греческий ученый, который первым вычислил окружность Земли, пользуясь методами геометрии. Он был чрезвычайно любознательным человеком. Прославился своими работами по математике, географии, философии и литературе. Заведовал Александрийской библиотекой в Египте (одной из первых библиотек в мире).ЭРАТОСФЕН
Слайд 4 Книги в то время представляли собой не
книги в нашем понимании этого слова, а папирусные свитки. В
знаменитой библиотеке хранилось более 700 000 свитков, которые содержали все сведения о мире, известные людям той эпохи. При содействии своих помощников Эратосфен первым рассортировал свитки по темам.Он дожил до глубокой старости. Когда он ослеп от старости, то перестал есть и умер от голода. Он не представлял себе жизни без возможности работать со своими любимыми книгами.
Слайд 5 В математике Эратосфена интересовал вопрос о том, как
найти все простые числа среди натуральных чисел от 1
до .(Эратосфен считал 1 простым числом. Сейчас математики считают 1 числом особого вида, которое не относится ни к простым, ни к составным числам.)
Эратосфен изобрел системный метод определения простых чисел путем отбора и отбрасывания чисел, имеющих делители, - все оставшиеся числа являются простыми. Этот метод впоследствии получил название решето Эратосфена и используется до сих пор, однако при работе с большими числами он неудобен, поскольку требуется слишком много времени, чтобы проверить наличие у них делителей.
Слайд 6
Почему «Решето»?
* * *
Так как во времена Эратосфена
писали на восковых табличках и не вычеркивали, а "выкалывали"
цифры, то табличка после описанного процесса напоминала решето. Поэтому метод Эратосфена для нахождения простых чисел получил название "решето Эратосфена".
Слайд 7
Какими бывают числа?
Просто́е число́ — это натуральное число,
которое имеет ровно два натуральных делителя (только 1 и
самого себя). Все остальные числа, кроме единицы, называются составными. Таким образом, все натуральные числа большие единицы разбиваются на простые и составные.Простое число
Слайд 8
Натуральное число
Натура́льные чи́сла (естественные числа) — числа,
возникающие естественным образом при счёте .
Существуют два подхода к
определению натуральных чисел — числа, используемые при:перечислении (нумеровании) предметов (первый, второй, третий…) — подход, общепринятый в большинстве стран мира (в том числе и в России);
обозначении количества предметов (нет предметов, один предмет, два предмета…).
Отрицательные и нецелые числа натуральными числами не являются.
***
Множество всех натуральных чисел принято обозначать знаком N. Множество натуральных чисел является бесконечным, так как для любого натурального числа найдётся большее его натуральное число.
Слайд 9
Составное число
Составное число́ — натуральное число большее 1, не
являющееся простым. Каждое составное число является произведением двух натуральных
чисел, больших 1.***
Последовательность составных чисел начинается так:
4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, …
Слайд 10
Как работать с Решетом Эратосфена?
Итак, это алгоритм нахождения
всех простых чисел не больше заданного числа N (пусть
N=100)Следуя методу Эратосфена, нужно выполнить следующие шаги:
Выписать подряд все натуральные числа от 2 до N (число 2 в списке-простое)
Как работать с Решетом Эратосфена?