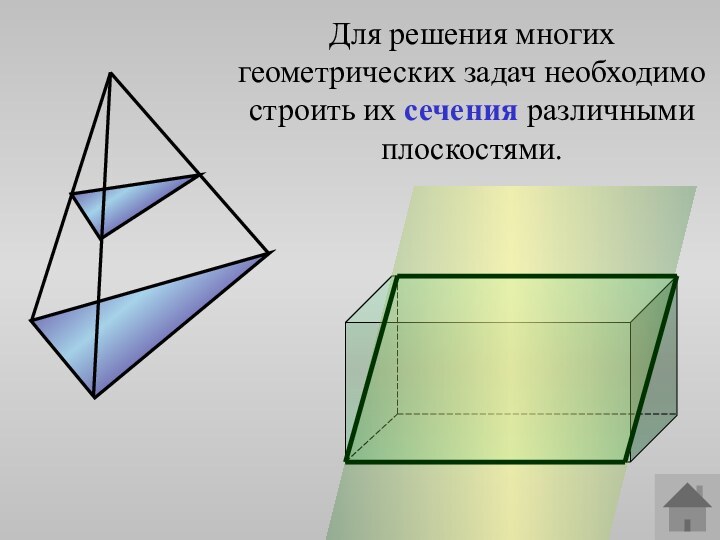
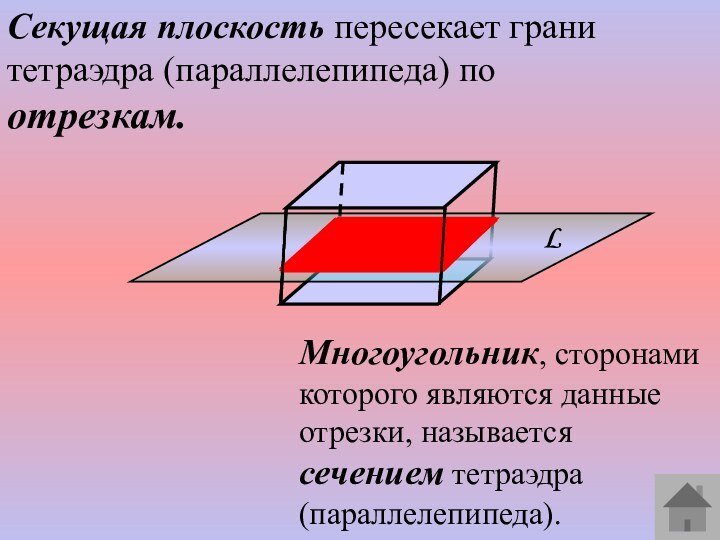
сечений тетраэдра.
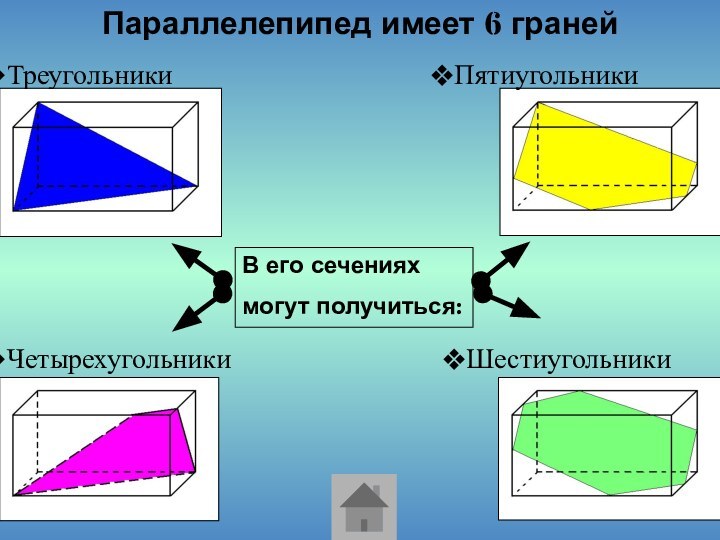
Виды сечений параллелепипеда.
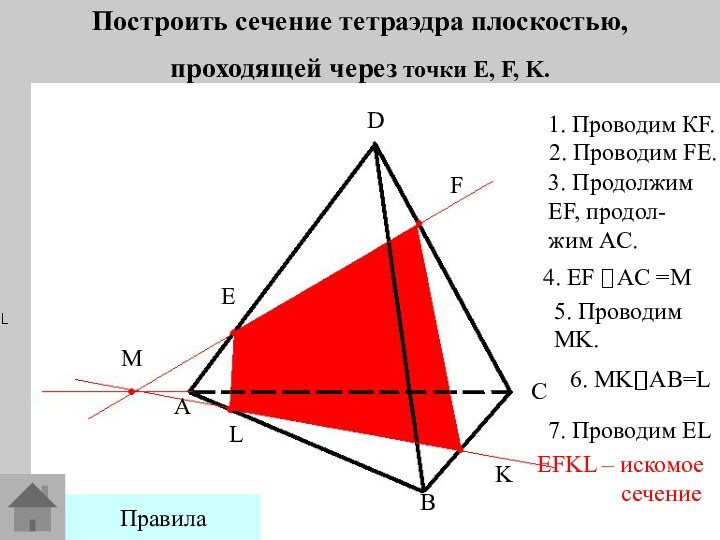
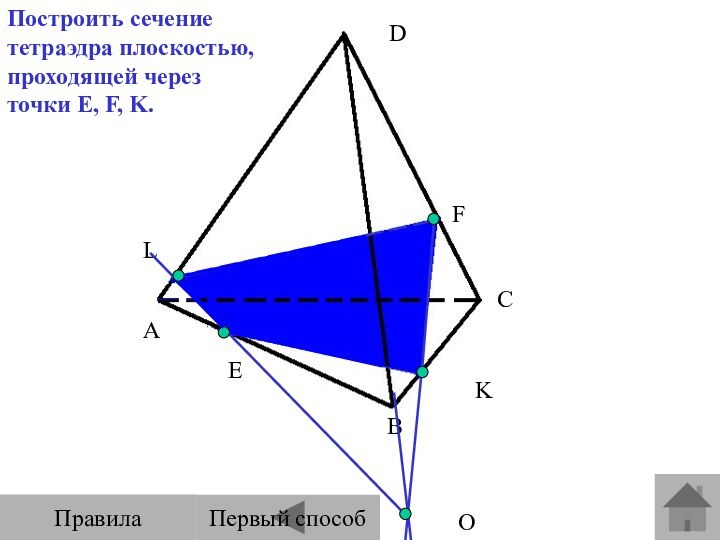
Задача на построение сечения тетраэдра с
объяснением.Задача на построение сечения тетраэдра с объяснением.
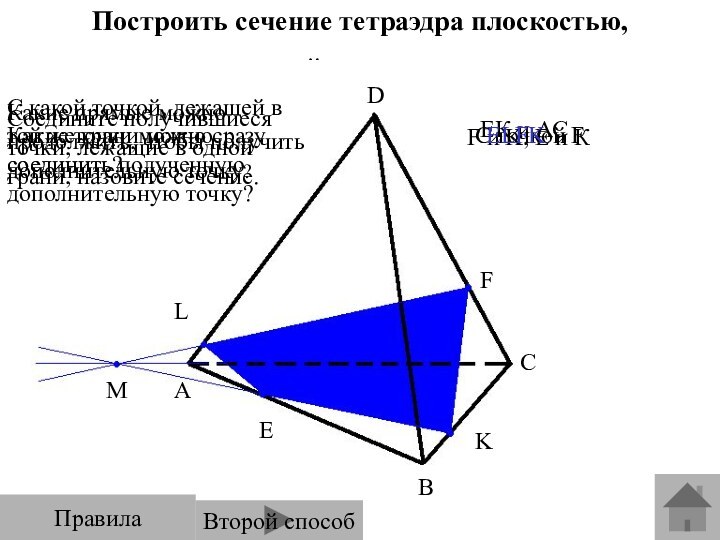
Задача на построение сечения тетраэдра по наводящим вопросам.
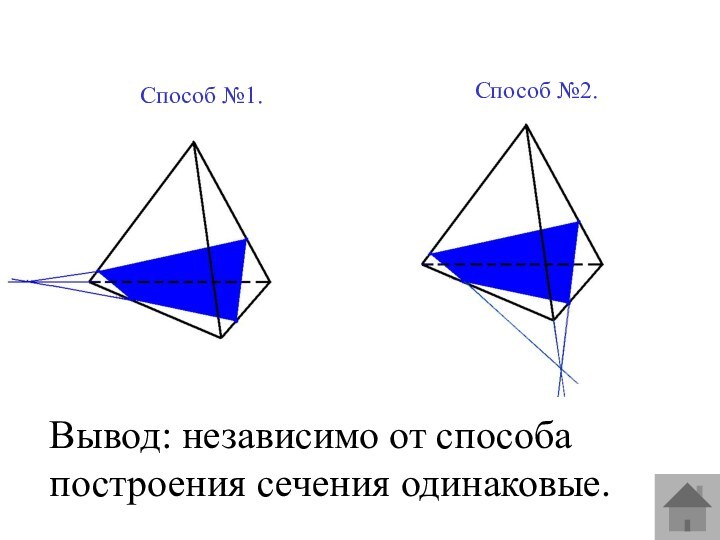
Второй вариант решения предыдущей задачи.
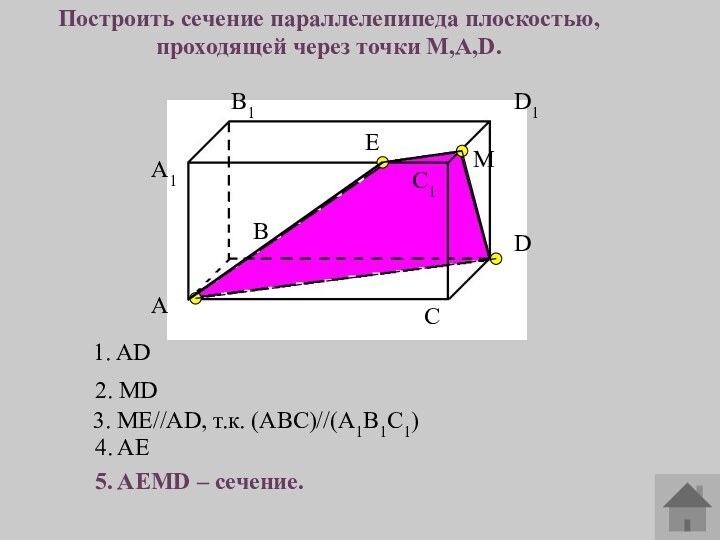
Задача на построение сечения параллелепипеда.
Задача на построение сечения параллелепипеда.
Пожелание учащимся.