Презентация на тему Шесть вопросов по планиметрии

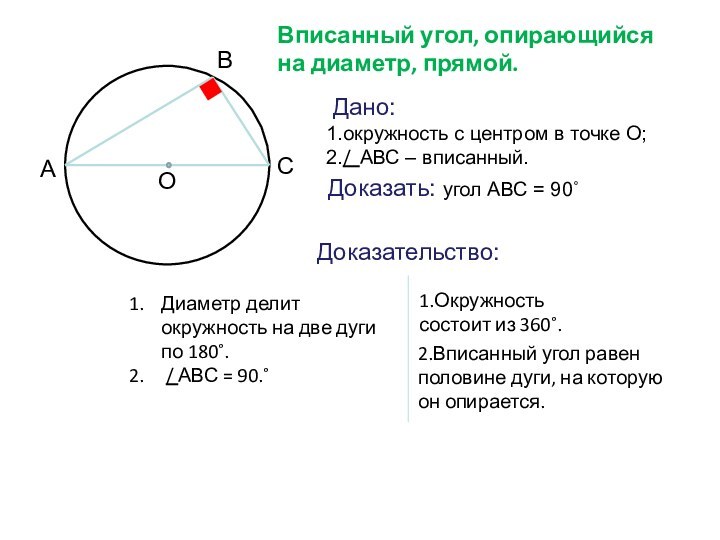
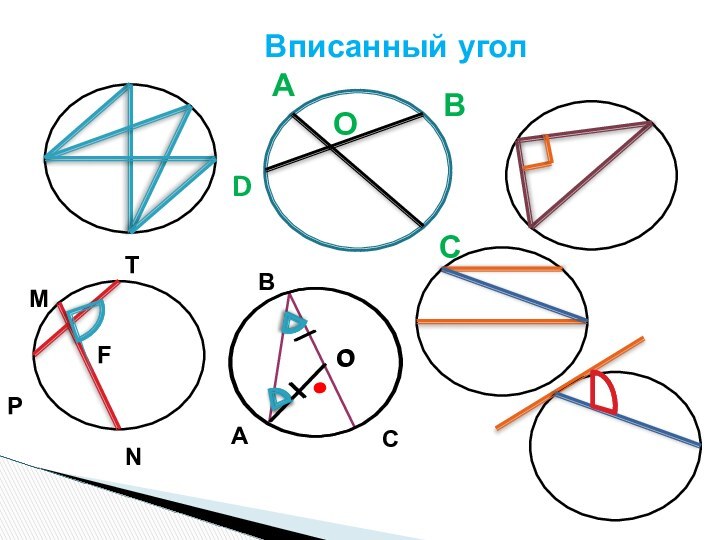
на две дуги по 180˚.
/ АВС = 90.˚
1.Окружность состоит

2.Вписанный угол равен половине дуги, на которую он опирается.

Дано:
окружность с центром в точке О;
/  АВС – вписанный.

Доказать: угол АВС = 90˚

Доказательство:

суммы катетов без гипотенузы
ВС, АС, АВ – касательные к

1)
Отрезки касательных, проведённых к окружности из одной точки, равны
Радиус окружности, проведенный в точку касания, перпендикулярен касательной
По условию, следует из пункта 3

5) По условию, следует из пункта 4

а

с

в

Дано: ΔАВС со сторонами а,в,с , r – радиус вписанной окружности

Доказать: r = ½ (а + в - с )

А

С

В

Доказательство:

r

К

Р

N

– точка пересечения отрезка АВ и перпендикулярного диаметра
Доказать:АС=ВС
Доказательство:
1)

АОВ-равнобедренный
*АО=ВО=R
2) ОС-его

3) ОС-биссектриса и медиана

4)АС=ВС

= 2 : (AB - CD)
1.Угол К =

А

B

D

С

K

α

Угол К является внутренним углом треуголника АKD.
Вписанный угол равен половине дуги, на которую он опирается.
См. п. 2.
Следует из п.2 и 3.

Доказательство