Презентация на тему симетрія

Кальян, вигукнув: “Як ви будуєте такі високі мінарети?” –

“Дуже просто”, - відповів Ходжа

Притча про осьову симетрію

Спочатку викопуємо
глибокий колодязь,
а потім вивертаємо
його навиворіт

Насреддін. І, хизуючись своєю дотепністю, пояснив:

n, якщо ця пряма перпендикулярна до відрізка ХХ′ і

проходить через його середину.
Пряма n є серединним перпендикуляром до відрізка ХХ′ і називається віссю симетрії.

А і В, D і Е, F і К

не є симетричними відносно прямої g.
Покажіть точку, симетричну точці О відносно прямої g.

В
n
А→А1, В → В1, АВ → А1В1

таке перетворення фігури F у фігуру F′, внаслідок якого

кожна точка Х фігури F переходить у точку Х′ фігури F′, симетричну точці Х відносно прямої a.

a

O

X

F

F′

X′

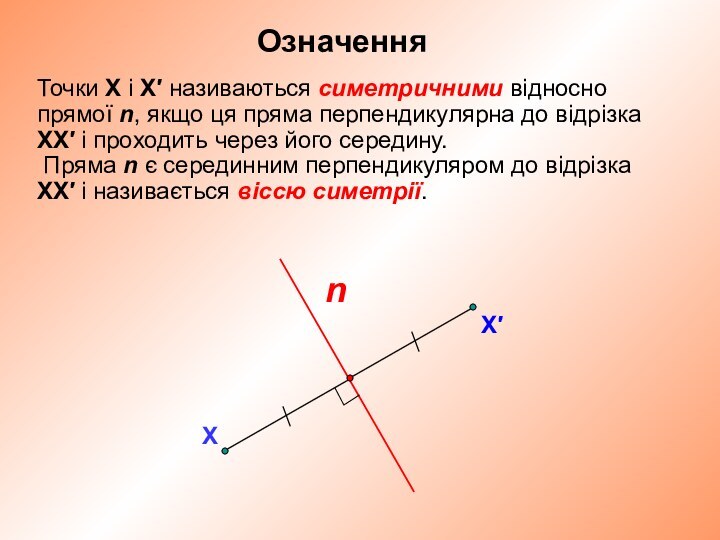
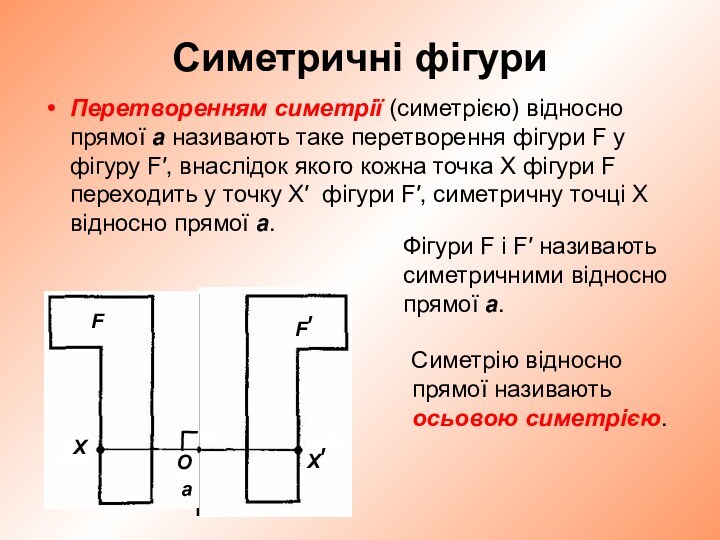
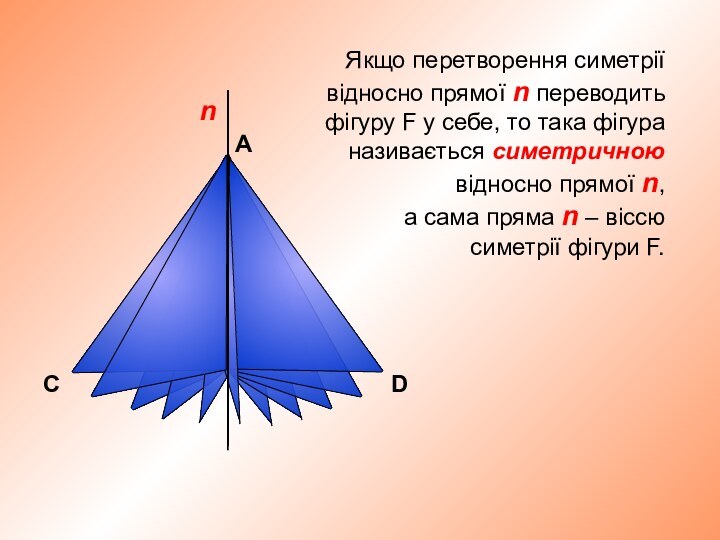
Симетрію відносно прямої називають осьовою симетрією.

Фігури F і F′ називають симетричними відносно прямої a.

а
Пряма а – вісь симетрії
А
С
В
a
А→А1, С→С1, В→В1,
∆АВС→∆А1В1С1

АВС відносно прямої a

А

В

a

С

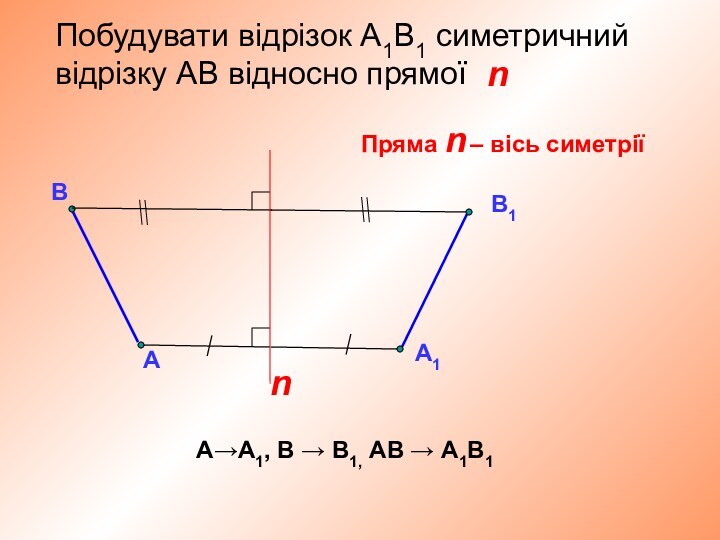
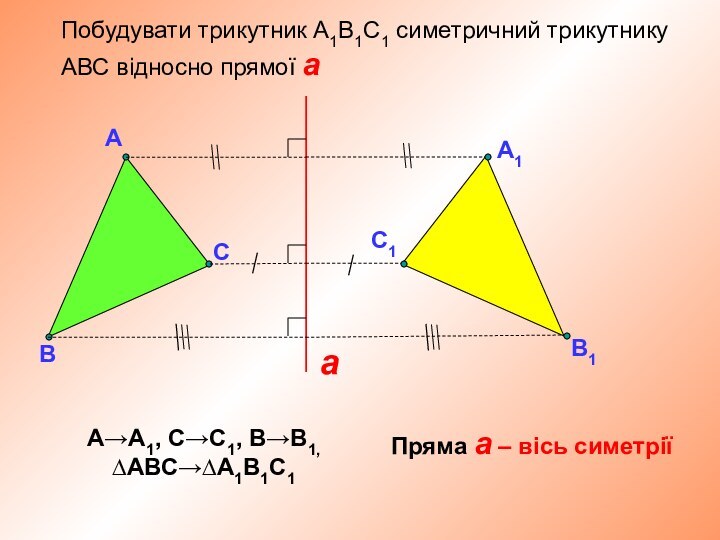
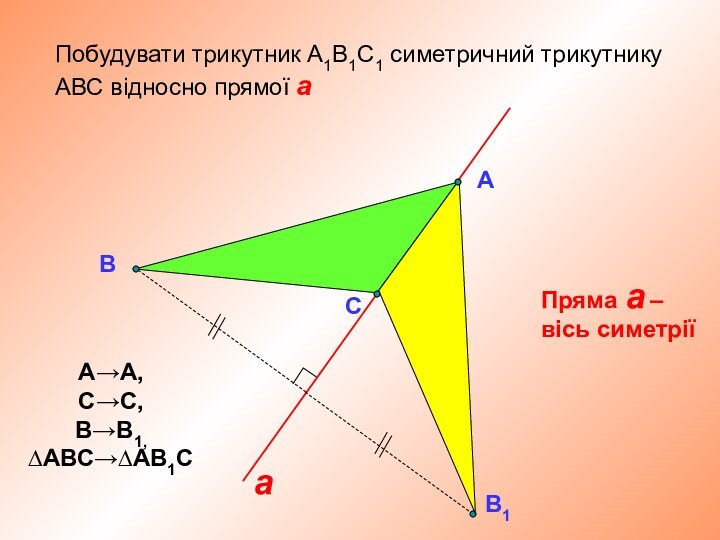
А→А,
С→С,
В→В1,
∆АВС→∆АВ1С

F у себе, то така фігура називається симетричною відносно

прямої n,
а сама пряма n – віссю симетрії фігури F.

А

D

n

симетричними відносно певної осі?
Назвіть номери фігур, що мають одну,

дві, три, чотири, безліч осей симетрії.
Скільки осей симетрії мають прямокутник і ромб?

n: точка Х – переходить в точку Х′, точка

Y переходить у точку Y′.
n=Оу.
Тоді: Х (х1;у1)→Х′(-х1;у1), Y(х2;у2)→Y′(-х2;у2).

x

Х(x1;y1)

y

O

Х′(-x1;y1)

Y(x2;y2)

Y′(-x2;y2)

Відстань між точками:
ХY=

Х′Y′=
Отже, ХY = Х′Y′.

Теорема
Осьова симетрія є переміщенням.

Осьова симетрія перетворює пряму на пряму; відрізок – на

відрізок; многокутник – на рівний йому многокутник.
3)Точки, що належать осі симетрії, відображаються самі на себе.
4)Якщо точки М(х;у) і N(х1; у1) симетричні відносно:
А) осі Ох, то виконується умова: х1=х, у1=-у;
Б) осі Оу, то виконується умова х1=-х, у1=у.

називається симетрією відносно даної прямої?
Яка фігура називається симетричною відносно

даної прямої?
Що таке вісь симетрії? Наведіть приклади.